Cylinder (geometry)
A cylinder (Latin cylindrus, ancient Greek κύλινδρος kýlindros , from κυλίνδειν kylíndein , 'roll', 'wallow') is in the simplest case one
- Area whose points have the same distance from a fixed straight line, the axis .
Since such an area is infinitely extended, it is usually cut with two parallel planes of distance (see picture).
- If the cutting planes are perpendicular to the axis, a vertical (or straight) circular cylinder with radius and height is created . The surface trimmed in this way is called the outer surface of the cylinder, the cut surfaces perpendicular to the axis can each be referred to as the base surface .
Since a straight circular cylinder can also be imagined to be generated by rotating a distance around the (parallel) cylinder axis, it is also called a rotary cylinder . The generating lines are called the surface lines of the cylinder or generating lines .
In engineering , a cylinder is often understood to be the body that is enclosed by the lateral surface and the two circular cutting surfaces.
In mathematics , a cylinder is defined more generally (see section on general cylinders )
Circular cylinder
In practice, the vertical circular cylinder in various variations plays an important role. Therefore, specific formulas are given for this.
Vertical circular cylinder
It arises for
- the volume (base × height)
- the outer surface (the development is a rectangle of length and height )
- the surface
A straight circular cylinder with is called an equilateral cylinder . This designation is explained as follows: If you cut such a cylinder with a plane that contains the cylinder axis, you get a square (with the side length ).
If the cross-section is an ellipse with the semiaxes , then is
- There is no simple formula for the surface area.
Hollow cylinder
If a straight circular cylinder has a bore along its axis, it is called a hollow cylinder . For a hollow cylinder - for example a straight piece of pipe - the determining parameters are the height, the outer radius and the inner radius . The wall thickness b is thus .
- The volume is
- the outer surface (inside and outside)
- the surface
If the height of a hollow cylinder is smaller than its outer radius , it is referred to as a perforated disc with a concentric , circular opening.
Cylinder section
If you cut a straight circular cylinder (radius ) with a plane at an angle, an ellipse is created as the intersection curve. If the lower cylinder section has the minimum height and the maximum height , then the cut ellipse has
- the major semi-axis and the minor semi-axis , where is, with the inclination angle of the cutting plane,
- the numerical eccentricity .
The cylinder section itself has
- the volume ,
- the outer surface
- the surface .
Note: The volume and the surface area are the same as that of the cylinder with the middle height .
Volume calculation of a horizontal circular cylinder (tank problem)
The calculation of the content of a partially filled horizontal circular cylinder can be made on the basis of the length , the radius and the filling level . According to the above equation volume = base · height , the volume of filling is calculated by multiplying the surface area of the circle segment with the length of the cylinder:
- .
General cylinder
In mathematics, a cylinder (shell) is defined more generally:
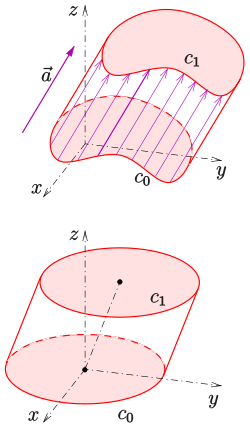
- A plane curve in a plane is shifted a fixed distance along a straight line that is not contained in. Two corresponding points of the curves and the shifted curve are connected by a segment. The entirety of these parallel lines forms the associated cylinder surface (see picture). The curve is called the guide curve . A straight line lying on the cylinder is called the generating line or surface line .
If the curve is a circle, an oblique circular cylinder is created . If is, the result is a vertical circular cylinder.
Is a closed curve, may be regarded as a back surface of a body, the peripheral surface with the two boundary surfaces. If the curve is not closed, e.g. B. a parabolic arc (see below), the cylinder is only the outer surface explained above, which can, however, be part of a surface of a body.
The geometric peculiarity of a cylinder surface consists in the following fact:
- A cylindrical surface contains straight, it is a ruled surface , and can not distorted in the plane of handled be.
This property in particular makes the cylinder surface interesting for the production of sheet metal cladding.
- If the generating curve is a polygon, one speaks of a prism (see examples).
Properties of a general cylinder
Volume, lateral surface and surface of a general cylinder are calculated as follows:
- Volume : if is a closed curve,
- where is the base area (of the enclosed area) and the height (see Cavalier principle ).
In the case of a prism, the base area can either be calculated directly (rectangle) or by a suitable division into triangles and / or rectangles (see area ). If the curve is piecewise smooth, the content can be determined directly or numerically using suitable integrals.
- where the circumference ( arc length ) of the cross-section (intersection curve to the surface lines) and the length of the surface (see picture). Note: can be understood as a vertical parallel projection of the guide curve on any cross-sectional plane (perpendicular to the surface lines).
For a vertical cylinder, and is the length of the guide curve .
For an inclined cylinder, the height is where is the angle of the cylinder axis (direction from ) and the normal of the plane . In the case of an oblique circular or elliptical cylinder, the cross-sectional curve is an ellipse, in the case of a prism a polygon. The scope is simply in a polygon the sum of the edge lengths in a circle . In the case of a piecewise smooth guide curve , one can try to calculate the length of the cross-sectional curve with the help of a curve integral . But even with an ellipse that is not a circle, this is already a problem (see elliptic integral ) that can only be solved numerically.
- Surface : if is a closed curve.
Analytical description
The outer surface of a vertical circular cylinder with radius and height , which is on the xy plane and has the z-axis as its axis, can be described by an equation in x, y and an inequality for z:
If you want to the full cylinder describe, you have to by having to replace.
If the equation of a circle is replaced by the equation of an ellipse , the description of a vertical elliptical cylinder is obtained:
- The volume is
A parametric representation of a vertical circular or elliptical cylinder is obtained by using the usual parametric representation of a circle or an ellipse:
It is difficult to give the equation of a cylinder that is freely supported in space. The parametric representation of any elliptical cylinder, on the other hand, is relatively simple:
Here, the center of the bottom ellipse and three linearly independent vectors. points in the direction of the cylinder axis (see picture).
If the three vectors are orthogonal in pairs and is , then the parametric representation describes a vertical circular cylinder with radius and height (see figure).
The fact that any elliptical cylinder always contains circles is shown in the circular section plane.
This type of parametric representation is very flexible. E.g. provides
represents a parabolic cylinder in a general position (see picture, parabola ).
A vertical parabolic cylinder can also be passed through in the same way as a vertical circular cylinder
describe.
The parametric representation
represents a hyperbolic cylinder in a general position (see hyperbola ).
A vertical hyperbolic cylinder can be passed through analogously to the vertical elliptical cylinder
describe.
Application examples
silo

Grain silos often have the shape of a cylinder.
A cylindrical silo with the diameter of 12 meters and the height is 60 meters to 40 percent with wheat filled. So it is and .
This gives the volume and the surface :
- Volume :
- Surface :
The grain silo is filled with around 2714 cubic meters of wheat . The surface is about 1131 square meters .
Drinking glass

Some drinking glasses have approximately the shape of a cylinder.
A cylindrical drinking glass with a diameter of 74 millimeters and a filling height of 92 millimeters is half filled with orange juice . So it is and .
This gives the volume and the surface :
- Volume :
- Surface :
The drinking glass is filled with about 198 milliliters of orange juice . The surface is about 193 square centimeters .
See also
- Development (descriptive geometry)
- Quadric
- Intersection (Descriptive Geometry)
- Steinmetz body (section of two or three full cylinders)
literature
- Bronstein-Semendjajew: Paperback of mathematics. Harri-Deutsch-Verlag, 1983, ISBN 3-87144-492-8 , p. 251.
- Arnfried Kemnitz: Mathematics at the beginning of your studies: Basic knowledge for all technical, mathematical, natural-scientific and economic courses . Springer, 2010, ISBN 978-3-8348-1293-3 , pp. 154–157 ( excerpt (Google) ).
Web links
- mathematik.tu-darmstadt.de Hartmann: Computer-assisted performing and constructive geometry , Uni Darmstadt, p. 99.
- math.kit.edu Renner: lateral surfaces of oblique bodies KIT Karlsruhe
- uni-regensburg.de Rothmeier: Geometrical bodies , University of Regensburg