Circular section plane

3-axis ellipsoid with a circle as a plane section

A circuit section plane is in the geometry of a plane (in 3-dimensional space) which is a quadric ( ellipsoid , hyperboloid , ...) in a circle intersect. A sphere is cut in a circle by every plane with which it has at least 2 points in common. The position is also simple for rotational quadrics (rotational ellipsoid, hyperboloid, paraboloid, cylinder, ...): They are cut in circles by all planes that are perpendicular to the axis of rotation, if they have at least 2 points in common. The position of 3-axis ellipsoids, genuinely elliptical hyperboloids, paraboloids, cylinders, ... is no longer obvious , although there are even more intersection circles in these asymmetrical cases. The following applies:

• Every quadric (area in 3-dimensional space) that contains ellipses also contains circles (see below).

Quadrics that are not included are: 1) parabolic cylinder , 2) hyperbolic cylinder, and 3)  hyperbolic paraboloid . A comprehensive discussion of all cases is e.g. B. in the book by Grotemeyer (see literature ) included.

Circular sections of quadrics were previously used to create models (see #Weblinks ).

Circular sectional planes also play a role in crystallography .

Description of the method

To find the planes that intersect a quadric in a circle, two essential observations are used:

(K :) If the intersection of a quadric with a sphere (auxiliary sphere ) lies in a pair of planes (two intersecting planes), the intersection consists of two circles.

(P :) If a plane intersects a quadric in a circle, this is also the case for all planes parallel to it , which have at least two points in common with the quadric.

To find circles on a quadric, it is sufficient to find an auxiliary sphere that intersects the quadric in a pair of planes. Then the planes parallel to the planes provide two sets of intersection circles.

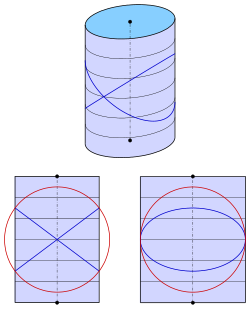
3-axis ellipsoid with circular cuts (blue and green) and the auxiliary sphere (red) that cuts the ellipsoid in the blue circles

Figure 1: Ellipsoid cut with spheres: ${\displaystyle c<{\color {SeaGreen}r_{1}}<{\color {Blue}b}<{\color {Purple}r_{2}}<a}$

3-axis ellipsoid

For the ellipsoid with the equation

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1}$

and the semi-axes one uses an auxiliary sphere with the equation ${\displaystyle a>b>c>0}$

${\displaystyle x^{2}+y^{2}+z^{2}=r^{2}\ .}$

The sphere radius must now be determined in such a way that the intersection of the ellipsoid and the sphere lies in a pair of planes through the origin . So that the absolute term falls out, one subtracts the spherical equation from the factor of the ellipsoid equation. It turns out ${\displaystyle r^{2}}$

${\displaystyle \left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}}{b^{2}}}-1\right)\;y^{2}+\left({\frac {r^{2}}{c^{2}}}-1\right)\;z^{2}=0\ .}$

This equation describes a pair of planes only if one of the three coefficients is zero. Both for and for there are equations that are only satisfied by points on the -axis or -axis. Only the case leads to a pair of planes with the equation ${\displaystyle r=a}$ ${\displaystyle r=c}$ ${\displaystyle x}$ ${\displaystyle z}$ ${\displaystyle r=b}$

• ${\displaystyle \left({\frac {b^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {b^{2}}{c^{2}}}-1\right)\;z^{2}=0\ \quad \Leftrightarrow \quad z=\pm {\frac {c}{a}}{\sqrt {\frac {a^{2}-b^{2}}{b^{2}-c^{2}}}}\;x\ ,}$

because only in this case do the remaining coefficients have different signs (because of ). ${\displaystyle a>b>c}$

Figure 1 shows how the cuts with unsuitable spheres look like: The radius is too large (magenta) or too small (cyan).

If the values ​​of the semi-axes and approach, the two sets of circles also approach. For (ellipsoid of revolution) all circular planes are orthogonal to the axis of rotation. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a=b>c}$

Proof of property (P):
If the ellipsoid is rotated around the -axis so that one of the two blue circles lies in the -plane, the ellipsoid suffices for one equation ${\displaystyle y}$ ${\displaystyle x-y}$

${\displaystyle Ax^{2}+By^{2}+Cz^{2}+D{\color {red}xz}=E}$

and for results . For this to be a circular equation, it must be true. If one now cuts the ellipsoid with a plane parallel to the plane with the equation , the result is ${\displaystyle z=0}$ ${\displaystyle Ax^{2}+By^{2}=E}$ ${\displaystyle A=B\neq 0,\ E>0}$ ${\displaystyle x-y}$ ${\displaystyle z=z_{0}}$

${\displaystyle A(x^{2}+y^{2})+Dz_{0}x=E-Cz_{0}^{2}}$.

This equation describes a circle or a point or the empty set. (The center and radius are obtained after completing the square .)

Elliptical single-shell hyperboloid

Single-shell hyperboloid

For the hyperboloid with the equation

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1\ ,\quad a>b\ ,c>0}$

one obtains (as with the ellipsoid) the equation for the intersection with a sphere ${\displaystyle x^{2}+y^{2}+z^{2}=r^{2}}$

${\displaystyle \left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}}{b^{2}}}-1\right)\;y^{2}-\left({\frac {r^{2}}{c^{2}}}+1\right)\;z^{2}=0\ .}$

This results in a pair of levels only for : ${\displaystyle r=a}$

${\displaystyle \left({\frac {a^{2}}{b^{2}}}-1\right)\;y^{2}-\left({\frac {a^{2}}{c^{2}}}+1\right)\;z^{2}=0\ \quad \Leftrightarrow \quad z=\pm {\frac {c}{b}}{\sqrt {\frac {a^{2}-b^{2}}{a^{2}+c^{2}}}}\;y}$

Elliptical cylinder

Elliptical cylinder

For the elliptical cylinder with the equation

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\ ,\quad a>b\ ,}$

one obtains the equation

${\displaystyle \left({\frac {r^{2}}{a^{2}}}-1\right)\;x^{2}+\left({\frac {r^{2}}{b^{2}}}-1\right)\;y^{2}-z^{2}=0\ .}$

There is a pair of levels only for : ${\displaystyle r=a}$

${\displaystyle \left({\frac {a^{2}}{b^{2}}}-1\right)\;y^{2}-z^{2}=0\ \quad \Leftrightarrow \quad z=\pm {\frac {\sqrt {a^{2}-b^{2}}}{b}}\;y}$

Remarks:

1. Since the above single-shell hyperboloid becomes the cylinder of this section, the circular planes of the cylinder result from those of the hyperboloid in this way. ${\displaystyle c\to \infty }$
2. An elliptical cylinder can therefore always be understood as an oblique circular cylinder .

Elliptical paraboloid

Figure 2: Elliptical paraboloid

For the elliptical paraboloid with the equation

${\displaystyle ax^{2}+by^{2}-z=0\ ,\quad a\,{\color {red}{<}}\,b\ ,}$

choose a sphere through the vertex with the center on the axis:

${\displaystyle x^{2}+y^{2}+(z-r)^{2}=r^{2}\quad \Leftrightarrow \quad x^{2}+y^{2}+z^{2}-2rz=0}$

After eliminating the linear term, the equation results

${\displaystyle (2ra-1)\;x^{2}+(2rb-1)\;y^{2}-z^{2}=0\ .}$

There is a pair of levels only for : ${\displaystyle r={\tfrac {1}{2a}}}$

${\displaystyle \left({\frac {b}{a}}-1\right)y^{2}-z^{2}=0\quad \Leftrightarrow \quad z=\pm {\sqrt {\frac {b-a}{a}}}\;y}$

Note:
The radius of the sphere is equal to the radius of the curvature of the further parabola (see Figure 2).

Elliptical double-shell hyperboloid

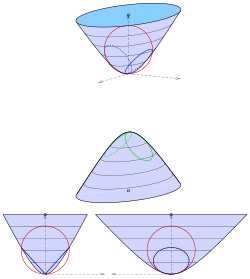
Figure 3: Elliptical double-shell hyperboloid

The double-shell hyperboloid with the equation

${\displaystyle -{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1\ ,\quad a>b\ ,\ c>0\ ,}$

it is advisable to move it so that a vertex is the origin (see Figure 3):

${\displaystyle -{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}+{\frac {(z+c)^{2}}{c^{2}}}=1\quad \Leftrightarrow \quad \ -{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}+{\frac {2z}{c}}=0}$

The sphere is also chosen in such a way that it contains the origin and its center point lies on the axis: ${\displaystyle z}$

${\displaystyle x^{2}+y^{2}+(z-r)^{2}=r^{2}\quad \Leftrightarrow \quad x^{2}+y^{2}+z^{2}-2zr=0}$

After eliminating the linear term, the equation results

${\displaystyle \left(-{\frac {r}{a^{2}}}+{\frac {1}{c}}\right)\;x^{2}+\left(-{\frac {r}{b^{2}}}+{\frac {1}{c}}\right)\;y^{2}+\left({\frac {r}{c^{2}}}+{\frac {1}{c}}\right)\;z^{2}=0\ .}$

There is a pair of levels only for : ${\displaystyle r={\tfrac {a^{2}}{c}}}$

${\displaystyle \left(-{\frac {a^{2}}{b^{2}c}}+{\frac {1}{c}}\right)\;y^{2}+\left({\frac {a^{2}}{c^{3}}}+{\frac {1}{c}}\right)\;z^{2}=0\ \quad \Leftrightarrow \quad z=\pm {\frac {c}{b}}{\sqrt {\frac {a^{2}-b^{2}}{a^{2}+c^{2}}}}\;y}$

Note:
The radius of the sphere is equal to the radius of the circle of curvature of the further hyperbola (see Figure 3).

Elliptical cone

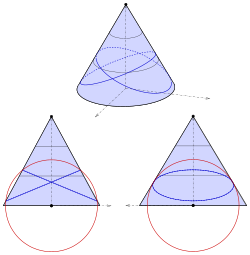
Figure 4: Elliptical cone

The elliptical cone with the equation

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-z^{2}=0\ ,\quad a>b\ ,}$

it is advisable to move it so that its tip is not at the origin (see Figure 4):

${\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-(z-1)^{2}=0\quad \Leftrightarrow \quad {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-z^{2}+2z=1.}$

Now you can use a sphere around the origin:

${\displaystyle x^{2}+y^{2}+z^{2}=r^{2}}$

The elimination of results in: ${\displaystyle x^{2}}$

${\displaystyle \left({\frac {a^{2}}{b^{2}}}-1\right)\;y^{2}-(1+a^{2})\;z^{2}+2a^{2}z=a^{2}-r^{2}}$

Since planes are to be expected that do not go through the origin, one carries out a quadratic addition and obtains:

${\displaystyle {\frac {a^{2}-b^{2}}{b^{2}}}\;y^{2}-(1+a^{2})\left(z-{\frac {a^{2}}{1+a^{2}}}\right)^{2}=a^{2}-{\frac {a^{4}}{1+a^{2}}}-r^{2}}$

For this equation to describe a pair of planes, the right-hand side must be zero; H. If you then dissolve, you get: ${\displaystyle r={\tfrac {a}{\sqrt {1+a^{2}}}}\ .}$ ${\displaystyle z}$

${\displaystyle z={\frac {a^{2}}{1+a^{2}}}\pm {\frac {1}{b}}{\sqrt {\frac {a^{2}-b^{2}}{1+a^{2}}}}\;y}$

Note:
An elliptical cone can always be understood as an oblique circular cone . One should note, however, that the straight line through the apex and the center of the circle is not the axis of the cone (axis of symmetry).

literature

• KP Grotemeyer : Analytical Geometry. Göschen-Verlag, 1962, p. 143.
• H. Scheid, W. Schwarz: Elements of linear algebra and analysis. Spektrum, Heidelberg, 2009, ISBN 978-3-8274-1971-2 , p. 132.

Individual evidence

1. ^ WH Westphal: Physical Dictionary: Two parts in one volume. Springer-Verlag, 1952, ISBN 978-3-662-12707-0 , p. 350.
2. ↑ H. Tertsch: The strength phenomena of the crystals. Springer-Verlag, Vienna, 1949, ISBN 978-3-211-80120-8 , p. 87.
3. ^ G. Masing: Textbook of general metal science. Springer-Verlag, Berlin, 1950, ISBN 978-3-642-52-993-1 , p. 355.

Web links

• H. Wiener, P. Treutlein: Directory of mathematical models. (PDF; 9.8 MB).