The quadratic extension is a method of transforming terms in which a variable occurs as a quadratic form, so that a squared binomial is created and the first or second binomial formula can be used. This method can be used, for example, to solve quadratic equations or to determine the vertex shape (and thus also the vertex , i.e. the extreme value ) of quadratic functions .
In analytical geometry , this method is one of the methods with which equations can be converted from quadrics to a normal form. In doing so, quadratic terms are transformed into several variables ( quadratic forms ).
Examples Determining the vertex shape of a quadratic function
Given quadratic function:
y
=
a
x
2
+
b
x
+
c
{\ displaystyle y = ax ^ {2} + bx + c \,}
Excluding the leading coefficient :
y
=
a
(
x
2
+
b
a
x
)
+
c
{\ displaystyle y = a \ left (x ^ {2} + {\ frac {b} {a}} x \ right) + c}
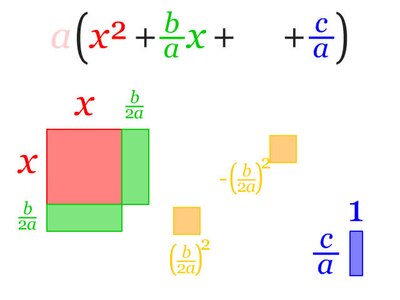
The parenthesized term is now brought into a form so that the first binomial formula can be used. It is referred to as “nutritious zero”, or “zero supplement”.
(
x
2
+
2
d
x
+
d
2
)
-
d
2
{\ displaystyle (x ^ {2} + 2dx + d ^ {2}) - d ^ {2}}
d
2
-
d
2
{\ displaystyle d ^ {2} -d ^ {2}}
Square addition:
y
=
a
(
x
2
+
b
a
x
+
(
b
2
a
)
2
-
(
b
2
a
)
2
)
+
c
{\ displaystyle y = a \ left (x ^ {2} + {\ frac {b} {a}} x + \ left ({\ frac {b} {2a}} \ right) ^ {2} - \ left ( {\ frac {b} {2a}} \ right) ^ {2} \ right) + c}
Formation of the square:
y
=
a
[
(
x
+
b
2
a
)
2
-
(
b
2
a
)
2
]
+
c
{\ displaystyle y = a \ left [\ left (x + {\ frac {b} {2a}} \ right) ^ {2} - \ left ({\ frac {b} {2a}} \ right) ^ {2 } \ right] + c}
Multiply out :
y
=
a
(
x
+
b
2
a
)
2
-
a
b
2
4th
a
2
+
c
{\ displaystyle y = a \ left (x + {\ frac {b} {2a}} \ right) ^ {2} - {\ frac {ab ^ {2}} {4a ^ {2}}} + c}
Vertex form of the function:
y
=
a
(
x
+
b
2
a
)
2
+
(
c
-
b
2
4th
a
)
{\ displaystyle y = a \ left (x + {\ frac {b} {2a}} \ right) ^ {2} + \ left (c - {\ frac {b ^ {2}} {4a}} \ right) }
Reading the vertex:
S.
(
-
b
2
a
|
c
-
b
2
4th
a
)
{\ displaystyle S \ left (- {\ frac {b} {2a}} \ right | \ left.c - {\ frac {b ^ {2}} {4a}} \ right)}
Addition: With is the coordinate of the vertex. The following then applies to the associated coordinate .
x
S.
=
-
b
/
(
2
a
)
{\ displaystyle x_ {S} = - b / (2a)}
x
S.
{\ displaystyle x_ {S}}
x
{\ displaystyle x}
y
{\ displaystyle y}
y
S.
{\ displaystyle y_ {S}}
y
S.
=
c
-
a
⋅
(
x
S.
)
2
{\ displaystyle y_ {S} = ca \ cdot (x_ {S}) ^ {2}}
example
Given quadratic function:
y
=
2
x
2
-
12
x
+
13
{\ displaystyle y = 2x ^ {2} -12x + 13 \,}
Excluding the leading coefficient:
y
=
2
(
x
2
-
6th
x
)
+
13
{\ displaystyle y = 2 (x ^ {2} -6x) +13 \,}
Because of the "nutritious zero" is inserted:
(
6th
2
)
2
=
9
{\ displaystyle ({\ tfrac {6} {2}}) ^ {2} = 9}
9
-
9
{\ displaystyle 9-9}
Square addition:
y
=
2
(
x
2
-
6th
x
+
9
-
9
)
+
13
{\ displaystyle y = 2 (x ^ {2} -6x + 9-9) +13 \,}
Formation of the square:
y
=
2
[
(
x
-
3
)
2
-
9
]
+
13
{\ displaystyle y = 2 [(x-3) ^ {2} -9] +13 \,}
Multiply out :
y
=
2
(
x
-
3
)
2
-
18th
+
13
{\ displaystyle y = 2 (x-3) ^ {2} -18 + 13 \,}
Vertex form of the function:
y
=
2
(
x
-
3
)
2
-
5
{\ displaystyle y = 2 (x-3) ^ {2} -5 \,}
Reading the vertex:
S.
(
3
|
-
5
)
{\ displaystyle S (3 | -5) \,}
Solving a quadratic equation
(The general rules for solving equations must be observed.)
Given quadratic equation:
2
x
2
-
12
x
=
32
{\ displaystyle 2x ^ {2} -12x = 32 \,}
Normalization:
x
2
-
6th
x
=
16
{\ displaystyle x ^ {2} -6x = 16 \,}
The left side of the equation is now shaped so that the second binomial formula can be applied. is also added on the right side of the equation:
x
2
-
2
d
x
+
d
2
{\ displaystyle x ^ {2} -2dx + d ^ {2}}
d
2
{\ displaystyle d ^ {2}}
Square addition:
x
2
-
6th
x
+
9
=
16
+
9
{\ displaystyle x ^ {2} -6x + 9 = 16 + 9 \,}
Formation of the square:
(
x
-
3
)
2
=
25th
{\ displaystyle (x-3) ^ {2} = 25 \,}
Root extraction :
x
-
3
=
±
5
{\ displaystyle x-3 = \ pm 5 \,}
Resolving the amount function :
x
-
3
=
-
5
{\ displaystyle x-3 = -5 \,}
x
-
3
=
5
{\ displaystyle x-3 = 5 \,}
Solution set :
L.
=
{
-
2
;
8th
}
{\ displaystyle \ mathbb {L} = \ {- 2; 8 \}}
Determination of an antiderivative The indefinite integral
∫
1
4th
x
2
-
8th
x
+
13
d
x
{\ displaystyle \ int {\ frac {1} {4x ^ {2} -8x + 13}} \, \ mathrm {d} x}
should be calculated. The square addition in the denominator gives
4th
x
2
-
8th
x
+
13
=
⋯
=
4th
(
x
-
1
)
2
+
9
.
{\ displaystyle 4x ^ {2} -8x + 13 = \ dotsb = 4 (x-1) ^ {2} +9 \ ,.}
For the integral this means:
∫
1
4th
x
2
-
8th
x
+
13
d
x
=
1
4th
∫
1
(
x
-
1
)
2
+
(
3
2
)
2
d
x
=
1
4th
⋅
2
3
arctan
2
(
x
-
1
)
3
+
C.
{\ displaystyle {\ begin {aligned} \ int {\ frac {1} {4x ^ {2} -8x + 13}} \, \ mathrm {d} x & = {\ frac {1} {4}} \ int {\ frac {1} {(x-1) ^ {2} + ({\ frac {3} {2}}) ^ {2}}} \, \ mathrm {d} x \\ & = {\ frac {1} {4}} \ cdot {\ frac {2} {3}} \ arctan {\ frac {2 (x-1)} {3}} + C \ end {aligned}}}
In the last transformation step above, the following known integral was used, which can be found in a table of antiderivatives :
∫
1
x
2
+
a
2
d
x
=
1
a
arctan
x
a
+
C.
{\ displaystyle \ int {\ frac {1} {x ^ {2} + a ^ {2}}} \, \ mathrm {d} x = {\ frac {1} {a}} \ arctan {\ frac { x} {a}} + C}
Normal form of a quadric The quadric
Q
=
{
(
x
,
y
)
∈
R.
2
∣
q
(
x
,
y
)
=
0
}
{\ displaystyle Q = \ {(x, y) \ in \ mathbb {R} ^ {2} \ mid q (x, y) = 0 \}}
q
(
x
,
y
)
=
x
2
+
4th
x
y
+
5
y
2
-
6th
x
-
14th
y
+
9
{\ displaystyle q (x, y) = x ^ {2} + 4xy + 5y ^ {2} -6x-14y + 9}
should be brought to affine normal form. Adding a square in the variable (i.e. , considered a parameter) and then adding a square in gives
x
{\ displaystyle x}
y
{\ displaystyle y}
y
{\ displaystyle y}
q
(
x
,
y
)
=
x
2
+
(
4th
y
-
6th
)
x
+
5
y
2
-
14th
y
+
9
=
x
2
+
(
4th
y
-
6th
)
x
+
(
2
y
-
3
)
2
-
(
2
y
-
3
)
2
+
5
y
2
-
14th
y
+
9
=
(
x
+
2
y
-
3
)
2
-
(
2
y
-
3
)
2
+
5
y
2
-
14th
y
+
9
=
(
x
+
2
y
-
3
)
2
+
y
2
-
2
y
=
(
x
+
2
y
-
3
)
2
+
y
2
-
2
y
+
1
2
-
1
2
=
(
x
+
2
y
-
3
)
2
+
(
y
-
1
)
2
-
1
{\ displaystyle {\ begin {aligned} q (x, y) & = x ^ {2} + (4y-6) x + 5y ^ {2} -14y + 9 \\ & = x ^ {2} + ( 4y-6) x + (2y-3) ^ {2} - (2y-3) ^ {2} + 5y ^ {2} -14y + 9 \\ & = (x + 2y-3) ^ {2} - (2y-3) ^ {2} + 5y ^ {2} -14y + 9 \\ & = (x + 2y-3) ^ {2} + y ^ {2} -2y \\ & = (x + 2y -3) ^ {2} + y ^ {2} -2y + 1 ^ {2} -1 ^ {2} \\ & = (x + 2y-3) ^ {2} + (y-1) ^ { 2} -1 \ end {aligned}}}
With the substitution , the equation of the quadric is transformed to the circle equation .
u
=
x
+
2
y
-
3
{\ displaystyle u = x + 2y-3}
v
=
y
-
1
{\ displaystyle v = y-1}
Q
{\ displaystyle Q}
u
2
+
v
2
=
1
{\ displaystyle u ^ {2} + v ^ {2} = 1}
Alternatives
The vertex form of a quadratic function can also be obtained with the help of differential calculus (by determining the zero of the first derivative).
For solving quadratic equations, there are ready-made solution formulas that you only have to insert. The derivation of these formulas is done using the quadratic addition.
literature FA Willers, KG Krapf: Elementary Mathematics: A preliminary course for higher mathematics . 14th edition. Springer, 2013, ISBN 978-3-642-86564-0 , pp. 84–86
Web links
<img src="https://de.wikipedia.org//de.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">





![y = a \ left [\ left (x + \ frac {b} {2a} \ right) ^ 2- \ left (\ frac {b} {2a} \ right) ^ 2 \ right] + c](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e139d56b23c94e36aeea97719d5984a71ee207c)














![y = 2 [(x-3) ^ 2-9] +13 \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/60f159e43eaaf02e1310cfde5c7bb494b42e47d9)























