Parabola (mathematics)
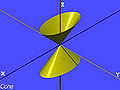
In mathematics , a parabola (via Latin parabola from ancient Greek παραβολή parabolḗ “juxtaposition, comparison, likeness, equality”; traced back to παρά pará “next to” and βάλλειν bállein “throw”) is a second-order curve and is therefore second via an algebraic equation Describable degree. In addition to the circle , the ellipse and the hyperbola, it is one of the conic sections : It is created when a straight circular cone intersects with a plane that runs parallel to a surface line and does not go through the apex of the cone. Because of this very special cutting requirement, the parabola plays a special role among the conic sections: It has only one focal point and all parabolas are similar to one another .
The parabola was discovered by Menaichmos and named by Apollonios von Perge (about 262–190 BC) as parabolic .
Parabolas often appear in mathematics as graphs of quadratic functions .
Parables also play a role in everyday life:
- The functioning of parabolic antennas and parabolic mirrors is based on the geometric property of the parabola to collect rays arriving parallel to its axis at the focal point (see below ).
- A stone thrown diagonally upwards moves approximately on a parabolic path, the throwing parabola (see bouncing ball, fountain). This is due to the fact that throwing movements are described by quadratic functions.
- In an airplane that moves along a trajectory parabola, there is weightlessness. Such parabolic flights are used for training astronauts.
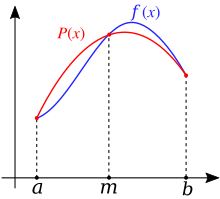
- In mathematics, parabolas are often used to approximate more complicated functions, since they are the simplest curved function graphs (equation:) after the straight lines (equation:) and can fit better than straight lines to curved function graphs. In the CAD area ( Computer Aided Design ), parabolas appear as Bézier curves . One advantage of parabolas over circles, ellipses and hyperbolas is that they can be described as a function graph of 2nd degree polynomial functions .
Definition with guideline
A parabola can be described geometrically as a locus :
- A parabola is the geometric location of all points whose distance from a special fixed point - the focal point - is the same as the distance from a special straight line - the guideline .
Notated as a set of points:
The point that lies in the middle between the focal point and the guide line is called the vertex or vertex of the parabola. The straight line connecting the focal point and vertex is also called the axis of the parabola. It is the only axis of symmetry of the parabola.
Leads to coordinate so that is the guideline and the equation has, then for from the equation
a parabola open upwards.
The half width of the parabola at the level of the focal point resulting from to and means (analogous to the ellipse, and hyperbola) of the half-parameter of the parabola. As with the ellipse (in the main vertex ) and hyperbola, the half-parameter is the vertex radius of curvature , i.e. the radius of the circle of curvature at the vertex. In the case of a parabola, there is also the distance between the focal point and the line. The equation of the parabola can thus also be written in the following form:
If you swap and , you get with
the equation of a parabola opened to the right.
By definition, a parabola is the equidistance curve to its focus and line.
Parabola as a function graph
A parabola open upwards or downwards with a vertex at the zero point (0,0) and the -axis as the axis is represented (in Cartesian coordinates) by an equation
described. For the parabolas are open upwards, for downwards (see picture). The following applies:
- The focal point is ,
- the half-parameter is ,
- the guideline has the equation and
- the tangent at the point has the equation .
For obtaining the normal parabola . Your focus is the half-parameter and the guideline has the equation .
After a shift one obtains the apex shape of any parabola that is open upwards or downwards:
- with the parting
By multiplying it out, the general equation of a parabola opened upwards or downwards results:
It is the graph of the quadratic function
- .
If the function is given, the vertex can be found by completing the square :
Every parabola is similar to the normal parabola y = x²
In terms of geometry, two figures are exactly similar to one another if they can be converted into one another through a similarity mapping. A similarity mapping is a sequential execution of centric extensions, shifts, rotations and reflections.
Any parabola has a vertex and can be transformed by displacement and a suitable rotation around the origin so that the transformed parabola has the origin as the vertex and the axis as the axis. So the parabola is similar to a parabola with the equation . Due to the additional centric stretching , the parabola is finally converted into the normal parabola . So it applies
- Every parabola is similar to the normal parabola.
Remarks:
- This statement is only correct for parabolas and not for ellipses / unit circles and hyperbolas / unit hyperbolas!
- There are other simple affine maps that map the parabola to the normal parabola. For example . But this illustration is not a similarity illustration !
Parabola as a special case of conic sections
The family of conic sections, whose axis is the -axis and which have a vertex at the origin (0,0) with the vertex curvature radius (arbitrary, but fixed), can be given by the equation
describe.
- For one obtains a circle (vertex curvature circle of all conic sections of the family),
- for an ellipse,
- for a parabola and
- for a hyperbola (see picture).
The general equation for conic sections is
- a, b, c not all 0.
In order to recognize which conic section is described by a specific equation, you have to carry out a major axis transformation (rotation and subsequent shift of the coordinate system). See also conic section .
Parabola as a conic section
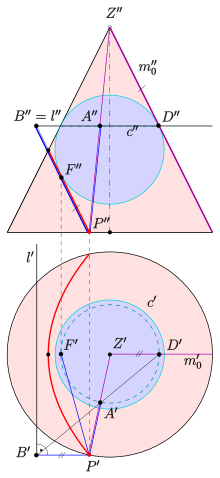
If you cut a straight circular cone with a plane whose inclination is equal to the inclination of the surface lines of the cone, a parabola results as an intersection curve (see picture, red curve). The proof of the defining property with regard to the focal point and guideline (see above) is carried out with the help of a Dandelin sphere , i.e. i. a sphere touching the cone in a circle and the parabola plane in a point . It turns out that the focal point of the parabola and the line of intersection of the plane of the circle of contact with the plane is the guideline .
- be any point on the intersection curve.
- The lines and are tangential to the sphere and are therefore of the same length.
- The planes through the surface line intersect the parabolic plane in a family of parallel straight lines that are perpendicular to the straight line ( !).
- Application of the theorem of rays to the intersecting straight lines and the parallel lines yields the equality of the length of the lines . (Note: are of the same length!).
- From the equality of the length of the lines and finally follows
- .
Thread construction of a parabola
The definition of a parabola with the help of the guideline offers a simple possibility to draw an arc of a parabola with the help of a thread and a right angle (here in a T-shape to slide along a straight line):
(0) Choosing the focal point and the guideline of the parabola to be drawn
(1) Thread of length (blue in the drawing)
(2) Fixing one end of the thread at the point of the ruler, the other end at the focal point
(3) Creating the angle so, that one leg can slide along the guideline
(4) Use a pen to stretch the thread so that it rests against the edge of the ruler
(5) By moving the ruler along the guideline, the pen sweeps over a parabolic curve, because it is always ( guideline property ).
Steiner generation of a parabola and the parabola that is dual to it
parabola
The following idea of constructing individual points of a parabola is based on Steiner's generation of a conic section (after the Swiss mathematician Jakob Steiner ):
- If there is a projective but not perspective mapping of one tuft to the other for two straight tufts in two points (all straight lines through the point or ) , the intersection points of assigned straight lines form a non-degenerate conic section.
For the generation of individual points of the parabola we start from the straight line at the vertex and the parallel line at the parallels to the -axis (i.e. the line at the far point of the -axis). Be it a point of the parabola and , . We divide the route into pieces of equal length and transfer this division into the direction of the route by means of a parallel projection (see picture). The parallel projection used provides the necessary projective mapping of the tuft in and of the parallel tuft . The points of intersection of the assigned straight line and the -th parallel to the -axis then lie on the parabola clearly determined by the specifications (see figure).
The proof is given by a simple calculation. See also: projective conic section .
Note: The left half of the parabola is obtained by mirroring it at the -axis.
Comment:
- Steiner generation is also available for ellipses and hyperbolas .
- Instead of the vertex of the parabola and the vertex tangent, you can also use any point and its tangent.
Dual parabola
- A dual parabola consists of the set of tangents of an (ordinary) parabola.
The previous Steiner generation of a parabola can be dualized, i.e. That is, the meaning of points and straight lines is reversed:
- If one has a projective, but not perspective, mapping of one row of points onto the other for two rows of points on two straight lines, then the straight lines connecting the assigned points form a dual conic section that has not degenerated (see Steiner's theorem ). The straight lines are also tangents, i.e. elements of the dual conic section.
In practice
- give three points ,
- divided both the track as well as in each case the same parts and numbers them in the picture.
- The straight lines are then the tangents of a parabola (the elements of a dual parabola).
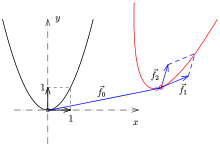
- The parabola is a Bezier curve of degree 2 with the points as control points .
Proof:
If the position vectors of the points are , then
the associated Bezier curve (parabola). The derivative (the tangent vector) is
Here, the parameters for the corresponding part points of the lines and . One calculates that is. So the straight line is tangent at the parabolic point .
Note: The proof also results from the first two steps of the De Casteljau algorithm for a Bezier curve of degree 2.
Parabola as an affine image of the normal parabola
Another definition of the parabola uses a special geometric mapping, namely affinity . Here a parabola is defined as an affine image of the normal parabola .
- Parametric representation
An affine mapping in the real plane has the form where is a regular matrix (determinant not 0) and is an arbitrary vector. If the column vectors are the matrix , the normal parabola becomes the parabola
pictured. is a point of the parabola and tangent vector at this point. stand i. A. not perpendicular to each other. That is, i. A. not the vertex of the parabola. But: The parabolic axis (symmetry axis through the vertex) is parallel to . This definition of a parabola provides a simple parametric representation of any parabola.
- Vertex, vertex shape
Since the vertex , the tangent to the parabola axis is vertical and the tangent direction at a point parabola is, the parameter results of the apex from the equation
- to .
The vertex shape of the parametric plot of the parabola is
- .
- Examples
- provides the usual parametric representation of the parabola .
- provides the parametric representation of the parabola, which results from rotating by the angle and then shifting by . The parametric representation is already in vertex form: The vertex is
- returns the parabola The parametric representation is not in vertex form. The vertex parameter is and the vertex shape is:
- implicit representation
Solving the parametric representation using Cramer's rule after and used , we obtain the implicit representation
- .
- Parabolas in space
If the vectors are out of the , a parametric representation of a parabola in space is obtained.
Affine self-mapping of the parabola y = x²
Not every affine mapping of the real affine plane (see previous section ) maps the norm parabola onto another parabola. The following affine mappings leave the parabola as a whole invariant:
These are the only affine maps that leave the parabola invariant.
To prove it: Set and apply the 1st binomial formula.
Special cases:
- For every point of the plane remains fixed. This image is called identity.
- For each point of the parabola is moved, i.e. i.e. there is no fixed point on the parabola.
- For the mapping is involutor, i. i.e., executed twice, it is the identity. Such an image is called an oblique reflection, because a straight line, namely , remains fixed point by point (see section “ Centers of parallel chords ”). In this case, there is exactly one fixed point on the parabola: . Only in this case is an oblique reflection a "normal" reflection on the axis.
Remark: If the real affine plane is supplemented by a distance line and its far points to form a projective plane and the far point of the -axis is added to the parabola , a projective conic section that has not degenerated is obtained and more images, projective collineations, are available. E.g. the projective collineation leaves with
the thus extended parabola invariant. This mapping is involutorial, leaves the parabolic points fixed and exchanges the parabolic point with the far point of the -axis.
properties
Focus
If a ray , which is incident parallel to the axis, at the parabola - d. H. at its tangent - mirrored, the reflected ray goes through the focal point. This reflected ray is also called the focal line or focal ray of the parabolic point in question. A paraboloid of revolution also has the corresponding property , i.e. the surface that arises when a parabola is rotated around its axis; it is often used in technology (see parabolic mirrors ).
In order to demonstrate this property of a parabola, one starts with a parabola of form . This is not a limitation, as any parabola can be represented in a suitable coordinate system. The tangent in a parabolic point has the equation (The slope of the tangent results from the derivative .) The tangent intersects the axis in the point . The focus is . The nadir point of the solder of the Guideline is . For a parabola is . From the coordinates of the points given in the picture you can see that is. The square is thus a diamond and the tangent is a diagonal of this diamond and thus a bisector. It follows from this:
- The focal ray is the reflection of the incident ray at the tangent / parabola.
The proof and the drawing show a possibility of constructing the tangent in a parabolic point with the help of the focal point, the guideline and the diamond . (More tangent constructions are contained in the section Tangent construction .)
Centers of parallel tendons
For every parabola the following applies:
- The midpoints of parallel tendons (see picture) lie on a straight line. This straight line is parallel to the parabolic axis.
This means that for every pair of points of a chord there is an oblique reflection on a straight line , which swaps the points and maps the parabola onto itself. An oblique reflection is understood to be a generalization of an ordinary reflection on a straight line , in which all points-to-image points are parallel to one another but not necessarily perpendicular to the mirror axis . If the chords are perpendicular to the parabolic axis, the straight line is the parabolic axis and the oblique reflection is an ordinary reflection.
The easiest way to verify this property is to use the normal parabola . Since all parabolas are affine images of the normal parabola (see above) and, in the case of an affine mapping, midpoints of lines pass into the midpoints of image lines, the above property applies to all parabolas.
Point construction
Any parabola can be described by an equation in a suitable coordinate system .
Another way of constructing parabolic points requires knowledge of three parabolic points and the direction of the parabolic axis:
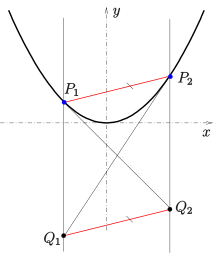
The following applies to a parabola : Are
- four points of the parabola and
- the intersection of the secant with the straight line as well as
- the intersection of the secant with the straight line (see picture),
then the secant is parallel to the straight line . and are parallels to the parabolic axis.
If the three points of a parabola are given, then by specifying a straight line through (not parallel to the parabola axis and no tangent) with this property, the parabola point can be constructed on this straight line.
As a proof: Since only intersection, connection and parallelism play a role, the proof can be carried out on the affine equivalent normal parabola . A short calculation shows that the straight line is parallel to the straight line .
Note: This property of a parabola is an affine version of the 5-point degeneration of Pascal's theorem .
Tangent construction
Any parabola can be described by an equation in a suitable coordinate system .
1st method
The following applies to a parabola :
- Are three points of the parabola and
- the intersection of the secant with the straight line , as well as
- the intersection of the secant with the straight line (see picture),
- then the tangent at the point is parallel to the straight line .
- ( and are parallels to the parabolic axis.)
This property can be used to construct the tangent at the point .
For the proof: Since only intersection, connection and parallelism play a role, the proof can be carried out on the affine equivalent normal parabola . A short calculation shows that the straight line has the slope . This is the slope of the tangent at the point .
Note: This property of a parabola is an affine version of the 4-point degeneration of Pascal's theorem .
2nd method
A second way of constructing the tangent at a point is based on the following property of a parabola :
- Are two points of the parabola and
- the intersection of the tangent in with the straight line , as well as
- the intersection of the tangent with the straight line (see picture),
- then the secant is parallel to the straight line .
- ( and are parallels to the parabolic axis.)
As a proof: Since only intersection, connection and parallelism play a role, the proof can be carried out on the affine equivalent normal parabola .
Note: This property of a parabola is an affine version of the 3-point degeneration of Pascal's theorem .
Axis direction construction
With the point construction and the tangent construction (see above) the axis direction of the parabola is assumed to be known. If the direction of the axis is not known, it can be either
- 1) with the help of the midpoints of two parallel chords (see above) or
- 2) with the help of the following property of a parabola, which requires the knowledge of two parabolic points and their tangents,
to construct.
Any parabola can be described by an equation in a suitable coordinate system .
The following applies to a parabola : Are
- two points of the parabola,
- the associated tangents,
- the intersection of the two tangents ,
- the intersection of the parallel to through the point with the parallel to through (see picture),
then the straight line is parallel to the parabolic axis and has the equation
For proof: As with the previous parabola properties, one can calculate the proof for the normal parabola .
Note: The property described here is an affine version of the 3-tangent degeneracy of Brianchon's theorem .
Pole-polar relationship
A parabola can always be described in a suitable coordinate system by an equation of the form . The equation of the tangent in a parabolic point is . If one allows in the right part of the equation that any point of the plane is, then becomes
- the straight line is assigned to the point .
And vice versa you can
- assign the point to the straight line .
Such an assignment point <-> straight line is called a polarity or pole-polar relationship . The pole is the point, the polar is the corresponding straight line.
The meaning of this pole-polar relationship is that the possible intersection points of the polar with the parabola are the points of contact of the tangents through the pole to the parabola.
- If the point (pole) lies on the parabola, its polar is the tangent at this point (see picture:) .
- If the pole lies outside the parabola, the points of intersection of the polar with the parabola are the points of contact of the tangents through the pole to the parabola (see picture:) .
- If the point lies within the parabola, its polar does not have an intersection with the parabola (see picture: and ).
For proof: The determination of the intersection of the polar of a point with the parabola and the search for parabola points whose tangents contain the point lead to the same quadratic equation.
Comment:
- The point of intersection of two polars (e.g. in the picture:) is the pole of the straight line connecting the associated poles (here:) .
- The focus and line are polar to one another.
- Straight lines parallel to the parabolic axis have no poles. They say: "Your poles are on the long-distance straight ."
Note: Pole-polar relationships also exist for ellipses and hyperbolas. See also projective conic section .
Orthogonal tangents
A parabola has the following property:
- Tangents orthogonal to one another intersect on the guideline.
The geometric location of all points at which tangents of a given curve intersect orthogonally is called the orthoptic curve . In the case of a parabola, its guideline is the associated orthoptic curve.
Base curve
The Fußpunktkurve (engl .: pedal curve ) of a (regular) curve is the sum of Lotfußpunkte from a fixed point , the pole, from the tangent of the curve. The following applies to a parabola:
- The base point curve of a parabola with respect to its focal point as a pole is the tangent at the vertex.
Proof:
The focal point of the parabola is the point . The tangent in any parabolic point has the equation
For the assertion is correct, so that in the following it can be assumed.
The perpendicular from the focal point to the tangent has the equation
So for the intersection of the tangent with the perpendicular,
be fulfilled for what is only possible for .
More generally, base point curves with one pole on the symmetry axis of the parabola are cissoids . There are four special cases. In addition to the above case with the focal point as the pole, the cissoids of Diocles are obtained for the vertex as the pole, the (straight) strophoids for the focal point reflected at the vertex as the pole and the trisectrix of Maclaurin for the focal point reflected at the line as the pole .
Parabolas of the form y = ax² + bx + c
Peripheral angle set for parabolas
Parabolas of form are function graphs that are uniquely determined by the 3 parameters . So you need 3 points to determine these parameters. A quick method is based on the set of peripheral angles for parabolas.
A angle to be measured between two chords we perform two straight lines which are not to be parallel axis, a square , a:
- For two lines we measure the corresponding angle with the number .
Two straight lines are parallel if and therefore the angular dimension = 0.
Analogous to the set of peripheral angles for circles, the applies here
Peripheral angle set (for parabolas):
- For four points (see picture) the following applies:
- The four points only lie on a parabola of the form if the angles at and in the above angle measure are equal, i.e. i.e. if
(Proof by recalculation. One can assume for one direction that the points lie on a parabola .)
3-point shape of a parabola
Analogous to the 2-point shape of a straight line (gradient angles are measured with the gradient), the set of peripheral angles for parabolas results in
3-point form (for parabolas):
- The equation of the parabola through 3 points is obtained by solving the equation
- after y.
Parabola in polar coordinates
A parabola described by in Cartesian coordinates satisfies the equation in polar coordinates
Your focus is . If the origin of the coordinates is placed in its focal point, the polar equation applies to it
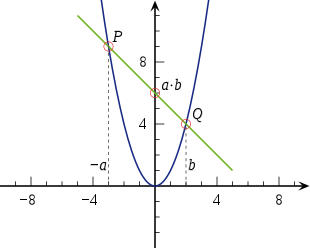
Graphic multiplication
A normal parabola is a "multiplication machine": you can use it to graphically calculate the product of two numbers. To do this, first draw the normal parabola in a Cartesian coordinate system. The factors to be multiplied are plotted on the axis and a point on the parabola is determined for each value. If the numbers are marked with and , there are two points and . The straight line goes through and intersects the axis at a point whose coordinate has the value . In the borderline case , the straight line is a tangent to the parabola.
If and have the same sign, it is more practical to apply one of the factors in a negative direction instead of later reversing the sign of the result, as happened in the example with the values and . Here you enter the factors as values with different signs in the coordinate system, namely as and . If you connect the points with a straight line, you can see that the intersection of the straight line with the -axis is 6 = 2 · 3 .
Parabola and chain line
Chain lines are similar to parabolas, but they are not. The rope of a suspension bridge, which sags due to its own weight, describes a chain line. This is not described by a quadratic function, but by the hyperbolic cosine . Mathematically, the similarity is expressed in that the hyperbolic cosine is in line
lets develop. The first two terms (red) describe a parabola and can be used as an approximation of the cosh function for small .
Parabolas as quadratic Bezier curves
A quadratic Bézier curve is a curve whose parametric representation is determined by three points , and :
This curve is an arc of a parabola (see section: Parabola as an affine image of the normal parabola).
Parabolas and Numerical Integration
In numerical integration , the value of a certain integral is approximated by approximating the graph of the function to be integrated using parabola arcs and integrating them. This leads to the Simpson rule , see picture.
The quality of the approximation is increased by increasing the subdivision and replacing the graph with a corresponding number of parabolic arcs and integrating them.
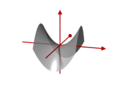
Parabolas as plane sections of quadrics
The following second-order surfaces ( quadrics ) have parabolas as plane sections:
- Elliptical cone (see also conic section )
- Parabolic cylinder
- Elliptical paraboloid
- Hyperbolic paraboloid
- Single-shell hyperboloid
- Double-shell hyperboloid
Laguerre plane: geometry of the parabolas
In the classical case, a Laguerre plane is an incidence structure that essentially describes the geometry of the curves , that is, parabolas and straight lines, in the real plane of observation. Not only straight lines, but also parabolas are available as connecting curves. For example, in a Laguerre plane there is exactly one connecting curve for three points with different x coordinates.
Parabola as trisectrix
A parabola can also be used as a trisectrix , which means that it can be used as an additional aid to precisely divide any angle into three with a compass and ruler . It should be noted that this does not contradict the impossibility of dividing angles into three parts with a compass and ruler, since according to the classic rules for constructions with compasses and ruler the use of parabolas is not allowed.
To divide one, you place your leg on the x -axis so that the vertex lies at the origin of the coordinate system. The coordinate system also contains the graph of the parabola . From the point of intersection of the unit circle around the origin with the second angle leg , the perpendicular falls on the y- axis. The perpendicular perpendicular to the perpendicular and the tangent to the unit circle in the point intersect at a point . Then the circle cuts the parabola with the radius and the perpendicular from to the x -axis cuts the unit circle in . The angle is now exactly one third of the starting angle .
The correctness of this construction can be proven by showing that the x -coordinate of has the value . The system of equations consisting of the equation of the circle around C and the parabola yields the cubic equation for the x coordinate of . Based on the trigonometric identity one can see immediately that there is a solution to the cubic equation.
This type of triangular division goes back to René Descartes , who described it in his book La Geometria (1637).
Higher order parabola
A parabola of order is understood to be the graph of a polynomial -th degree (in contrast to the graph of an exponential function or a square root function, ...). A 3rd order parabola is also called a cubic parabola .
So: Only in the case is a higher order parabola an ordinary parabola.
Neil's parable
The semicubical parabola or semikubische parable is an algebraic curve of 3rd order:
- Cartesian coordinate equation: with a real parameter
- Explicit:
It is not a parable in the usual sense; d. H. no conic section.
Parabola y = x² over any number field
If one considers the set of points in an affine plane over any (commutative) body that satisfies the parabolic equation, many properties of the real normal parabola remain, which are formulated with "intersect", "connect" and "parallel" and whose proofs are only multiplication / Use division and addition / subtraction. E.g .:
- A straight line intersects the parabola in at most two points.
- Through each parabolic point there (next to the line ) just a straight line with the parabola only point in common, the tangent : . A straight line without an intersection is called a passer-by , a straight line with two intersections is called a secant .
Differences to the real case:
- For (rational numbers) the straight line is a passerby, because the equation has no solution.
- There are no passers-by for (complex numbers). E.g .: intersects the parabola at the points .
- If the body has characteristic 2 (i.e. it is true ), there are no secants among the straight lines , since every equation in the case of characteristic 2 has at most one solution (there is no “ ”). The tangent at the parabolic point has (for characteristic 2) the equation . That is, all tangents are parallel to the axis.
See also
literature
- Peter Proff: The interpretation of the terms "ellipse", "parabola" and "hyperbola" according to Apollonios v. Perge. In: “Gelêrter der arzeniê, ouch apotêker”. Contributions to the history of science. Festschrift for the 70th birthday of Willem F. Daems. Edited by Gundolf Keil, Horst Wellm Verlag, Pattensen / Hanover 1982 (= Würzburg medical-historical research, 24), ISBN 3-921456-35-5 , pp. 17–34.
Web links
- Geogebra: parabola
- Parabolas. On: mathematische-basteleien.de.
- Parabola . In: Serlo .
- Frans van Schooten: Mathematische Oeffeningen , 1659
Individual evidence
- ^ Wilhelm Gemoll : Greek-German school and hand dictionary . G. Freytag Verlag / Hölder-Pichler-Tempsky, Munich / Vienna 1965.
- ↑ Peter Proff: The interpretation of the terms "ellipse", "parabola" and "hyperbola" according to Apollonios v. Perge. In: Gundolf Keil (ed.): "Gelêrter der arzeniê, ouch apotêker". Contributions to the history of science. Festschrift for the 70th birthday of Willem F. Daems. Horst Wellm Verlag, Pattensen / Hanover 1982 (= Würzburg Medical History Research, 24), ISBN 3-921456-35-5 , pp. 17–34; here p. 17.
- ^ Frans van Schooten : Mathematische Oeffeningen , Leyden, 1659, p. 334
- ↑ Erich Hartmann: Projective Geometry. (PDF; 180 kB). Short script, Uni Darmstadt, p. 16.
- ^ Jacob Steiner's lectures on synthetic geometry. BG Teubner, Leipzig 1867 ( at Google Books ), Part 2, p. 96.
- ↑ a b Dörte Haftendorn: Exploring and understanding curves: With GeoGebra and other tools . Springer, 2016, ISBN 9783658147495 , pp. 258-261
- ↑ CDKG: Computer-assisted Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 107.
- ↑ CDKG: Computer-Aided Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 95.
- ↑ CDKG: Computer-assisted Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 117.
- ↑ CDKG: Computer-Aided Descriptive and Constructive Geometry (TU Darmstadt) (PDF; 3.4 MB), p. 123.
- ^ Robert C. Yates: The Trisection Problem . National Mathematics Magazine, Vol. 15, No. 4 (Jan., 1941), pp. 191-202 ( JSTOR )
- ^ Robert C. Yates: The Trisection Problem, 5. The Parabola. In: ERIC. National Council of Teachers of Mathematics, Inc., Washington, DC, 1971, pp. 35-37 , accessed June 19, 2019 .
- ↑ Erich Hartmann: Projective Geometry. (PDF; 180 kB). Short script, Uni Darmstadt, pp. 12-16.




































































































































































































































![r (\ varphi) = 4f \ frac {\ cos (\ varphi)} {\ sin ^ 2 (\ varphi)} \ quad \ text {with} \ varphi \ in \ left [- \ tfrac {\ pi} {2 }, \ tfrac {\ pi} {2} \ right] \ setminus \ {0 \}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd8c9ccd2730a42a13d046e0e0c317b2282037e3)



















![\ begin {align} \ vec c (t) \ & = \ \ sum_ {i = 0} ^ 2 \ binom 2 it ^ i (1-t) ^ {2-i} \ vec p_i \\ \ & = \ (1 - t) ^ {2} \ vec p_0 + 2t (1 - t) \ vec p_1 + t ^ {2} \ vec p_2 \\ \ & = \ (\ vec p_0-2 \ vec p_1 + \ vec p_2 ) t ^ {2} + (-2 \ vec p_0 + 2 \ vec p_1) t + \ vec p_0 \ text {,} t \ in [0,1] \ end {align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0156d961ce6bdb1e3296ec962a61d8b567b24547)