Pole and Polar

Pole and polar are a pair of terms in the plane geometry of conic sections : Each point on the plane is assigned a straight line that is reversible and unambiguous. The mediating element is a conic section. The straight line is called the polar of the point, the point the pole of the straight line. The mapping given by the assignment Pol↔Polare is called polarity , more precisely as hyperbolic projective polarity . For the more general term polarity see the article Correlation (Projective Geometry) , there the coordinate representation of polarities (as images) is explained.

Outside pole

Pole (red) outside the circle with polar (red) harmonic division: ${\displaystyle P}$ ${\displaystyle p}$
${\displaystyle {\frac {|AS|}{|BS|}}={\frac {|AP|}{|BP|}}}$

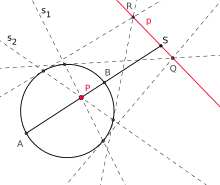
For a point that lies in the exterior of a non-degenerate conic section (in the picture: a circle ), there are always two tangents and that go through . If these touch the conic section at points and , the straight line is called “the polar to (with regard to the given conic section)”. ${\displaystyle {P}}$ ${\displaystyle t_{1}}$ ${\displaystyle t_{2}}$ ${\displaystyle {P}}$ ${\displaystyle T_{1}}$ ${\displaystyle T_{2}}$ ${\displaystyle p=T_{1}T_{2}}$ ${\displaystyle {P}}$

Conversely one can say:

Intersects a straight line (the polar ) a conic section in two points and , the point of intersection of the two tangents in means and the pole to (with respect to the conic section). ${\displaystyle {p}}$ ${\displaystyle {T_{1}}}$ ${\displaystyle {T_{2}}}$ ${\displaystyle {T_{1}}}$ ${\displaystyle {T_{2}}}$ ${\displaystyle {p}}$

Harmonic division and final definition

If you draw a secant through the pole that intersects the conic in and and the polar in , the points and the line divide harmoniously (see drawing). This allows the polar to be defined as follows: ${\displaystyle {P}}$ ${\displaystyle {A}}$ ${\displaystyle {B}}$ ${\displaystyle {S}}$ ${\displaystyle {S}}$ ${\displaystyle {P}}$ ${\displaystyle {\left[AB\right]}}$

“If one draws the secants to a non-degenerate conic section through a point (the pole), the fourth harmonic points , which (together with ) harmoniously divide the cut tendons , lie on a straight line. This straight line is called the polar to (with regard to the conic section). " ${\displaystyle {P}}$ ${\displaystyle {P}}$ ${\displaystyle {P}}$

This definition no longer assumes that it lies in the exterior of the conic section. According to this, there is also a well-defined polar for every point in the interior. ${\displaystyle {P}}$

Inner pole

Pole (red) within the circle with polar (red) harmonic division: ${\displaystyle P}$ ${\displaystyle p}$
${\displaystyle {\frac {|AS|}{|BS|}}={\frac {|AP|}{|BP|}}}$

Geometrically, the polar to a point inside a conic section is obtained by drawing (at least two) secants through (in the picture and ) and constructing the tangents at the end points of their chords. The intersections of these tangent lines (in the picture and ) lie on the polars. ${\displaystyle {P}}$ ${\displaystyle {P}}$ ${\displaystyle {s_{1}}}$ ${\displaystyle {s_{2}}}$ ${\displaystyle {Q}}$ ${\displaystyle {R}}$

Conversely, one can also say:

If the polar is passer-by of the conic section, then the polar of all points lying on it intersect in the pole of the straight line.

special cases

• If the pole lies on the conic line, the polar is the tangent at this point. (Or vice versa: If the polar tangent to the conic section, its pole is the point of contact.)
• The polar of the center is the infinitely distant straight line .
• Pole to a diameter is an infinitely distant point , namely the point whose direction is indicated by the (parallel!) Tangents at the end of the diameter.

Connection with the mirroring of circles

If the point is not the center of the circle, the polar to a point with respect to a circle can also be determined by mirroring the circle . ${\displaystyle Q}$ ${\displaystyle Q}$

The assignment between a pole and its polar with respect to a circle around assigns the straight line to the point ( ) , which goes through the mirror point in the mirroring of the circle and is perpendicular to the connecting straight line. Compare with the illustration below on the right. ${\displaystyle Q}$ ${\displaystyle q}$ ${\displaystyle k}$ ${\displaystyle O}$ ${\displaystyle Q}$ ${\displaystyle Q\neq O}$ ${\displaystyle q}$ ${\displaystyle P=\sigma (Q)}$ ${\displaystyle \sigma }$ ${\displaystyle k}$ ${\displaystyle OP}$

Higher dimensions

In three-dimensional space, the conic section is replaced as a mediating element by a second-order surface , in the simplest case a sphere. If the pole is an external point, there are not only two tangents from it, but in general a whole family of tangents which form a cone (not necessarily a circular cone!). This touches the surface of the second order in a line (more precisely: in a conic section - in the case of the sphere in a circle), and this line is the line of intersection of the surface of the second order with a plane - precisely the polar plane . This term replaces the term polar here .

Secants running through the pole also create a harmonic division here , and one can define, also for points in the interior of the surface of the second order , quite analogously to the two-dimensional case:

“If one draws the secants to a non-degenerate second-order surface through a point (the pole), the fourth harmonic points , which (together with ) the cut tendons harmoniously divide , lie on one plane. This plane is called the polar plane to (with respect to the surface of the second order). " ${\displaystyle {P}}$ ${\displaystyle {P}}$ ${\displaystyle {P}}$

The special cases also behave analogously.

Corresponding conceptualizations are also possible for rooms with more than three dimensions.

See also

• Pole-polar relation of an ellipse
• Pole-polar relationship of a hyperbola
• Pole-polar relationship of a parabola

literature

• Hermann Schaal: Linear Algebra and Analytical Geometry . 2nd revised edition. tape 1 . Vieweg, Braunschweig 1976, ISBN 3-528-03056-9 , pp. 224 ff .
• Karl Rohn, Erwin Papperitz: Textbook of the descriptive geometry . 1st edition. tape 1 . Salzwasser Verlag, Paderborn 2011, ISBN 978-3-86195-888-8 , p. 184 ff .

Web links

Commons : Poles and polars  - collection of images, videos and audio files

• cut-the-knot.org
• Eric W. Weisstein : Polar . In: MathWorld (English).

References and comments

1. ↑ In the case of a parabola or hyperbola, the point lies in the “outside” when the curve bends away from it, i.e. when it is convex when viewed from the point.
2. ↑ Schaal (1974).