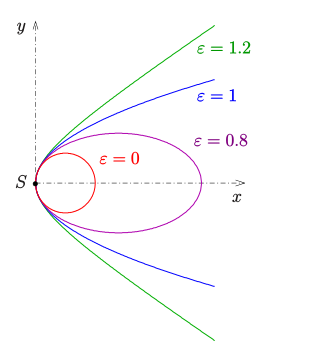
Hyperbola (math)

Hyperbola as a conic section:
( 1 ) provides the parabola, ( 2 ) circle and ellipse, ( 3 ) the hyperbola

Hyperbole in architecture: Brasilia Cathedral

In plane geometry , a hyperbola is a special curve that consists of two symmetrical branches that extend into infinity. In addition to the circle , the parabola and the ellipse, it is one of the conic sections that arise when a plane intersects with a straight circular cone (see picture).

Like ellipses and parabolas, hyperbolas can be defined as locus curves in the plane (see section Definition).

The hyperbola was discovered by Menaichmos . The name introduced by Apollonios von Perge comes from the Greek and refers to the exaggeration ( ὑπερβολή hyperbolé , from ancient Greek βάλλειν bállein , German ' to throw' , ὑπερβάλλειν hyperballein , German 'throwing over the target' ) of the numerical eccentricity (or the , see below) in the conic section: As the angle of intersection increases, the circle ( ) first transforms into increasingly elongated ellipses and then over the parabola ( and the intersecting plane is parallel to a tangential plane of the cone) into hyperbolas . ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon =0}$ ${\displaystyle \varepsilon =1}$ ${\displaystyle \varepsilon >1}$

Definition of a hyperbola as a locus

Hyperbola: definition and asymptotes

A hyperbola is defined as the set of all points on the plane of the drawing for which the amount of the difference between the distances to two given points, the so-called focal points and , is constantly equal : ${\displaystyle P}$ ${\displaystyle E^{2}}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle 2a}$

${\displaystyle H=\{P\in E^{2}\mid ||PF_{2}|-|PF_{1}||=2a\}}$

The center of the focal points is called the center of the hyperbola. The straight line connecting the focal points is the main axis of the hyperbola. On the main axis, the two vertices are at a distance from the center. The distance between the focal points and the center point is called the focal length or linear eccentricity and is usually referred to as. The dimensionless numerical eccentricity mentioned in the introduction is . ${\displaystyle M}$ ${\displaystyle S_{1},S_{2}}$ ${\displaystyle a}$ ${\displaystyle e}$ ${\displaystyle \varepsilon }$ ${\displaystyle {\tfrac {e}{a}}}$

The fact that the intersection of a straight circular cone with a plane that is steeper than the surface lines of the cone and does not contain the cone tip is a hyperbola is shown by demonstrating the above defining property with the help of Dandelin's spheres (see section Hyperbola as a conic section ).

Hyperbola: definition with a guide circle

Note:
The equation can also be interpreted as: Is the circle of radius , so has the district of the same distance as the focal point : It is called to be associated Leitkreis of hyperbole. He creates the right branch ${\displaystyle ||PF_{2}|-|PF_{1}||=2a}$ ${\displaystyle c_{2}}$ ${\displaystyle F_{2}}$ ${\displaystyle 2a}$ ${\displaystyle P}$ ${\displaystyle c_{2}}$ ${\displaystyle F_{1}}$ ${\displaystyle |Pc_{2}|=|PF_{1}|\ .}$ ${\displaystyle c_{2}}$ ${\displaystyle F_{2}}$

${\displaystyle H_{+}=\{P\in E^{2}\mid |Pc_{2}|=|PF_{1}|\}}$

the hyperbola. The left branch is obtained analogously with the guide circle belonging to the focal point . The creation of a hyperbola with guide circles should not be confused with the creation of a hyperbola with guidelines (see below ). ${\displaystyle H_{-}}$ ${\displaystyle F_{1}}$ ${\displaystyle c_{1}}$

Due to the guide circle property, a branch of a hyperbola is the equidistance curve to one of its focal points and the guide circle with the other focal point as the center.

Hyperbola in 1st main position

equation

The hyperbola equation takes on a particularly simple form if it is in the 1st main position , that is, the two focal points on the -axis are symmetrical to the origin; in the case of a hyperbola in the 1st principal position, the focal points have the coordinates and (with e = linear eccentricity), and the vertices have the coordinates and . ${\displaystyle x}$ ${\displaystyle (e,0)}$ ${\displaystyle (-e,0)}$ ${\displaystyle (a,0)}$ ${\displaystyle (-a,0)}$

For any point in the plane, the distance to the focal point is the same and to the other focal point . The point lies on the hyperbola if and only if the difference between these two expressions is equal or equal . ${\displaystyle (x,y)}$ ${\displaystyle (e,0)}$ ${\displaystyle {\sqrt {(x-e)^{2}+y^{2}}}}$ ${\displaystyle {\sqrt {(x+e)^{2}+y^{2}}}}$ ${\displaystyle (x,y)}$ ${\displaystyle 2a}$ ${\displaystyle -2a}$

By algebraic transformations and with the abbreviation one can show that the equation ${\displaystyle b^{2}=e^{2}-a^{2}}$

${\displaystyle {\sqrt {(x-e)^{2}+y^{2}}}-{\sqrt {(x+e)^{2}+y^{2}}}=\pm 2a}$

to the equation

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$

is equivalent. The latter equation is called the equation of the hyperbola in the 1st main position.

Parting

A hyperbola has only two vertices: and . In contrast to the ellipse, here and are no curve points. The latter are therefore also called imaginary side vertices. The straight line through the minor vertex is called the minor axis. The hyperbola is symmetrical to the major and minor axes. ${\displaystyle (a,0)}$ ${\displaystyle (-a,0)}$ ${\displaystyle (0,b)}$ ${\displaystyle (0,-b)}$

Asymptotes

Hyperbola: semi-axes a, b, lin. Eccentricity e, semi-parameters p

If one solves the hyperbola equation for , one obtains ${\displaystyle y}$

${\displaystyle y=\pm b{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}.}$

Here you can see that the hyperbola is attached to the straight line for magnitudes that are large ${\displaystyle x}$

${\displaystyle y=\pm {\frac {b}{a}}x}$

approximates arbitrarily close. These straight lines go through the center point and are called the asymptotes of the hyperbola ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1.}$

Half parameter p

Half the length of a hyperbolic tendon that goes through a focal point and runs perpendicular to the main axis is called the half-parameter (sometimes also the transverse dimension or just parameter ) of the hyperbola. He can be calculated by ${\displaystyle p}$

${\displaystyle p={\frac {b^{2}}{a}}.}$

Further meaning of : ${\displaystyle p}$

${\displaystyle p}$is the vertex curvature radius,

d. That is, is the radius of that circle through a vertex that best fits the hyperbola in the vertex. (See below: Formula collection / vertex equation .) ${\displaystyle p}$

tangent

The easiest way to find the equation of the tangent at a hyperbolic point is to implicitly differentiate the hyperbolic equation : ${\displaystyle (x_{B},y_{B})}$ ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$

${\displaystyle {\frac {2x}{a^{2}}}-{\frac {2yy'}{b^{2}}}=0\ \rightarrow \ y'={\frac {x}{y}}{\frac {b^{2}}{a^{2}}}\ \rightarrow \ y={\frac {x_{B}}{y_{B}}}{\frac {b^{2}}{a^{2}}}(x-x_{B})+y_{B}.}$

Taking into account : ${\displaystyle {\tfrac {x_{B}^{2}}{a^{2}}}-{\tfrac {y_{B}^{2}}{b^{2}}}=1}$

${\displaystyle {\frac {x_{B}}{a^{2}}}x-{\frac {y_{B}}{b^{2}}}y=1.}$

Equilateral hyperbola

A hyperbola that applies to is called an equilateral hyperbola. Their asymptotes are perpendicular to each other. The linear eccentricity is the numerical eccentricity and the half parameter is . ${\displaystyle a=b}$ ${\displaystyle e={\sqrt {2}}a}$ ${\displaystyle \varepsilon ={\sqrt {2}}}$ ${\displaystyle p=a}$

Parametric display with hyperbolic functions

The hyperbolic functions result in a parametric representation of the hyperbola (analogous to the ellipse) : ${\displaystyle \cosh ,\sinh }$ ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$

${\displaystyle (\pm a\cosh t,b\sinh t),\,t\in \mathbb {R} }$

Hyperbola in 2nd main position

If you swap and , you get hyperbolas in the 2nd main layer: ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1}$

Hyperbola with an equation y = A / x

Rotation of the coordinate system to describe an equilateral hyperbola as a graph of a function

3 equilateral hyperbolas with the coordinate axes as asymptotes red: A = 1, magenta: A = 2; blue: A = 3 ${\displaystyle y=A/x}$

If you rotate the xy coordinate system around the angle and name the new coordinates , then is . The equilateral hyperbola (the semiaxes are the same length!) Has the equation in the new coordinates . If you solve this equation for , you get ${\displaystyle -45^{\circ }}$ ${\displaystyle \xi ,\eta }$ ${\displaystyle x={\tfrac {\xi +\eta }{\sqrt {2}}},\;y={\tfrac {-\xi +\eta }{\sqrt {2}}}}$
${\displaystyle {\tfrac {x^{2}-y^{2}}{a^{2}}}=1}$ ${\displaystyle {\tfrac {2\xi \eta }{a^{2}}}=1}$ ${\displaystyle \eta }$ ${\displaystyle \eta ={\tfrac {a^{2}/2}{\xi }}\ .}$

So (in an xy coordinate system) is the graph of the function with the equation ${\displaystyle f\colon x\mapsto {\tfrac {A}{x}},\;A>0\;,}$

• ${\displaystyle y={\frac {A}{x}}\;,A>0,}$an equilateral hyperbola with
• the coordinate axes as asymptotes,
• the straight line as the main axis, ${\displaystyle y=x}$
• the center point and the semi-axes ${\displaystyle (0,0)}$ ${\displaystyle a=b={\sqrt {2A}},}$
• the parting ${\displaystyle ({\sqrt {A}},{\sqrt {A}}),(-{\sqrt {A}},-{\sqrt {A}}),}$
• the half-parameter and the vertex radius of curvature ${\displaystyle p=a={\sqrt {2A}},}$
• the linear eccentricity and the numerical eccentricity ${\displaystyle e=2{\sqrt {A}}}$ ${\displaystyle \varepsilon ={\sqrt {2}},}$
• the tangent at the point ${\displaystyle y=-{\tfrac {A}{x_{0}^{2}}}x+2{\tfrac {A}{x_{0}}}}$ ${\displaystyle (x_{0},A/x_{0}).}$

Turning the original hyperbola in order (this corresponds to a rotation of the coordinate system to ), one obtains an equilateral hyperbola with the equation ${\displaystyle -45^{\circ }}$ ${\displaystyle +45^{\circ }}$

• ${\displaystyle y={\frac {-A}{x}}\;,A>0}$ With
• the semi-axes ${\displaystyle a=b={\sqrt {2A}},}$
• the straight line as the main axis, ${\displaystyle y=-x}$
• the parting ${\displaystyle (-{\sqrt {A}},{\sqrt {A}}),({\sqrt {A}},-{\sqrt {A}}).}$

If the hyperbola is shifted with the equation so that the point is the center of the shifted hyperbola, the shifted hyperbola has the equation ${\displaystyle y={\frac {A}{x}}}$ ${\displaystyle (x_{0},y_{0})}$

• ${\displaystyle y={\frac {A}{x-x_{0}}}+y_{0}.}$

The shifted hyperbola has the asymptotes and . The parameters do not change when moved. ${\displaystyle x=x_{0}}$ ${\displaystyle y=y_{0}}$
${\displaystyle a,b,p,e,\varepsilon }$

Hyperbola as a conic section

Hyperbola (red): elevation and side elevation of a cone with Dandelin balls d ₁ , d ₂

If you cut a vertical circular cone with a plane whose inclination is greater than the inclination of the surface lines of the cone and which does not go through the tip of the cone, a hyperbola results as an intersection curve (see picture, red curve). The proof of the defining property with regard to the focal points (see above) is carried out with the help of two Dandelin spheres , these are spheres that touch the cone in circles or and the hyperbolic plane in points or . It turns out that the focal points are the intersection hyperbola. ${\displaystyle \pi }$ ${\displaystyle d_{1},d_{2}}$ ${\displaystyle c_{1}}$ ${\displaystyle c_{2}}$ ${\displaystyle F_{1}}$ ${\displaystyle F_{2}}$ ${\displaystyle F_{1},F_{2}}$

1. ${\displaystyle P}$ be any point on the intersection curve.
2. The surface line through cuts the circle in one point and the circle in one point . ${\displaystyle P}$ ${\displaystyle c_{1}}$ ${\displaystyle A}$ ${\displaystyle c_{2}}$ ${\displaystyle B}$
3. The lines and are tangential to the sphere and are therefore of the same length. ${\displaystyle {\overline {PF_{1}}}}$ ${\displaystyle {\overline {PA}}}$ ${\displaystyle d_{1}}$
4. The lines and are tangential to the sphere and are therefore of the same length. ${\displaystyle {\overline {PF_{2}}}}$ ${\displaystyle {\overline {PB}}}$ ${\displaystyle d_{2}}$
5. So is and thus independent of the hyperbola point . ${\displaystyle |PF_{1}|-|PF_{2}|=|PA|-|PB|=|AB|}$ ${\displaystyle P}$

Tangent as bisector

Hyperbola: Tangent as the bisector of the focal rays

The following applies to a hyperbola:

• The tangent at a point is the bisector of the focal rays ${\displaystyle P}$ ${\displaystyle {\overline {PF_{1}}},{\overline {PF_{2}}}.}$

It follows from this: A ray of light emanating from one focal point is reflected at the hyperbolic tangent in such a way that it appears to emanate from the other focal point.

proof

For the proof one uses the auxiliary point on the focal ray , which has the distance (see picture, is the semi-axis of the hyperbola). The straight line is the bisector of the focal rays. In order to prove that the tangent is in the point , one shows that any different point from cannot lie on the hyperbola. So the hyperbola can only intersect at the point and is therefore the tangent in . From the drawing it can be seen ( triangle inequality ) that is, i. h., it is . If there were a hyperbola point, the difference should be the same . ${\displaystyle L}$ ${\displaystyle {\overline {PF_{2}}}}$ ${\displaystyle F_{2}}$ ${\displaystyle 2a}$ ${\displaystyle a}$ ${\displaystyle w}$ ${\displaystyle w}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle w}$ ${\displaystyle w}$ ${\displaystyle P}$ ${\displaystyle P}$ ${\displaystyle |QF_{2}|<|LF_{2}|+|QL|=2a+|QF_{1}|}$ ${\displaystyle |QF_{2}|-|QF_{1}|<2a}$ ${\displaystyle Q}$ ${\displaystyle 2a}$

Since an angle bisector is easy to draw, this property offers a simple way of constructing the tangent in a hyperbolic point. If the two asymptotes are known instead of the two focal points, one can use the method described in the section on tangent construction.

Guidelines property

Hyperbola: guideline property

The term Direktrix or Leitlinie describes the two parallels to the minor axis at a distance . For any point on the hyperbola, the ratio between the distances to a focal point and the associated guideline is equal to the numerical eccentricity: ${\displaystyle d={\tfrac {a^{2}}{e}}}$ ${\displaystyle P}$

• ${\displaystyle {\frac {|PF_{1}|}{|Pl_{1}|}}={\frac {|PF_{2}|}{|Pl_{2}|}}=\varepsilon ={\frac {e}{a}}}$

To prove it , we show that for and the equation ${\displaystyle |PF_{1}|^{2}=(x-e)^{2}+y^{2},\ |Pl_{1}|^{2}=(x-{\tfrac {a^{2}}{e}})^{2}}$ ${\displaystyle y^{2}={\tfrac {b^{2}}{a^{2}}}x^{2}-b^{2}}$

${\displaystyle |PF_{1}|^{2}-{\tfrac {e^{2}}{a^{2}}}|Pl_{1}|^{2}=0}$

is satisfied.

Conversely, can be a point (a focal point) and a straight line (as a guideline) as well as a real number with specify and define a hyperbola as ${\displaystyle \varepsilon }$ ${\displaystyle \varepsilon >1}$

• Set of all points on the plane for which the ratio of the distances to the point and to the straight line is the same . ${\displaystyle \varepsilon }$

If you choose , you get a parabola . For results in an ellipse . ${\displaystyle \varepsilon =1}$ ${\displaystyle \varepsilon <1}$

To prove it, one assumes and the stipulation that there is a curve point. The guideline is then described by the equation . For follows from ${\displaystyle F_{1}=(f,0),\varepsilon >0}$ ${\displaystyle (0,0)}$ ${\displaystyle l_{1}}$ ${\displaystyle x=-{\tfrac {f}{\varepsilon }}}$ ${\displaystyle P=(x,y)}$ ${\displaystyle |PF_{1}|^{2}=\varepsilon ^{2}|Pl_{1}|^{2}}$

${\displaystyle (x-f)^{2}+y^{2}=\varepsilon ^{2}(x+{\tfrac {f}{e}})^{2}=(\varepsilon x+f)^{2}}$ and from here ${\displaystyle x^{2}(\varepsilon ^{2}-1)+2xf(1+\varepsilon )-y^{2}=0.}$

With the abbreviation you get ${\displaystyle p=f(1+\varepsilon )}$

${\displaystyle x^{2}(\varepsilon ^{2}-1)+2px-y^{2}=0.}$

This is the vertex equation of an ellipse ( ), a parabola ( ), or a hyperbola ( ). See the Formula Collection section . ${\displaystyle \varepsilon <1}$ ${\displaystyle \varepsilon =1}$ ${\displaystyle \varepsilon >1}$

If you introduce new constants in such a way that is, then the vertex equation goes into ${\displaystyle \varepsilon >1}$ ${\displaystyle a,b}$ ${\displaystyle \varepsilon ^{2}-1={\tfrac {b^{2}}{a^{2}}},\ p={\tfrac {b^{2}}{a}}}$

${\displaystyle {\tfrac {(x+a)^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$

over. This is the equation of a hyperbola with the center and axis as the main axis and semiaxes . ${\displaystyle (-a,0)}$ ${\displaystyle x}$ ${\displaystyle a,b}$

Thread construction of a hyperbola

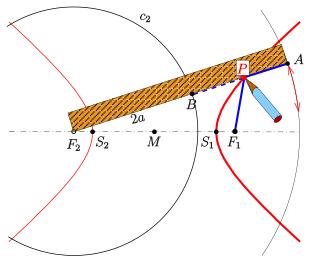
Hyperbola: thread construction

The definition of a hyperbola with the help of a guide circle ( see above ) offers a simple possibility to draw a hyperbola arc with the help of a thread and a ruler:

(0) Choice of the focal points and the spacing of the vertices; the radius of the guide circle is also (1) the ruler is rotatably attached with one end in the left focal point and the point is marked at a distance on the edge (2) thread (blue) the length (3) attachment of one end of the thread at the point of the ruler, the other end at the focal point (4) with a pen tension the thread so that it at the ruler edge rests (5) By turning of the ruler to the point of the pin sweeps a Hyperbelbogen, because it is ( Leitkreiseigenschaft ). ${\displaystyle F_{1},F_{2}}$ ${\displaystyle 2a}$ ${\displaystyle 2a}$
${\displaystyle B}$ ${\displaystyle 2a}$
${\displaystyle |AB|}$
${\displaystyle A}$ ${\displaystyle F_{1}}$
${\displaystyle AB}$
${\displaystyle F_{2}}$ ${\displaystyle |PF_{1}|=|PB|}$

Steiner generation of a hyperbola

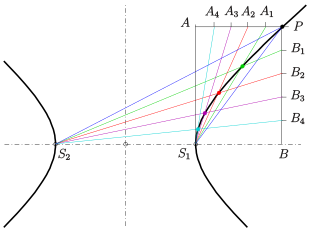
Hyperbola: Steiner generation

Hyperbola y = 1 / x: Steiner generation

The following idea of ​​constructing individual points of a hyperbola is based on Steiner's generation of a conic section (after the Swiss mathematician Jakob Steiner ):

If one has a projective but not perspective mapping of one tuft to the other for two straight tufts in two points (all straight lines through the point or ) , the intersection points of assigned straight lines form a non-degenerate conic section. ${\displaystyle S_{1},S_{2}}$ ${\displaystyle S_{1}}$ ${\displaystyle S_{2}}$ ${\displaystyle \pi }$

For the generation of individual points of the hyperbola , we start from the straight line tufts in the vertices . Now be a point of hyperbola and . We divide the side of the rectangle into n equal pieces and transfer this division to the line by means of a parallel projection in the direction of the diagonals (see picture). The parallel projection used provides the necessary projective mapping of the tufts in and . The intersection points of the assigned straight lines and then lie on the hyperbola that is clearly determined by the specifications. ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$ ${\displaystyle S_{1},S_{2}}$ ${\displaystyle P=(x_{0},y_{0})}$ ${\displaystyle A=(a,y_{0}),B=(x_{0},0)}$ ${\displaystyle {\overline {BP}}}$ ${\displaystyle AB}$ ${\displaystyle {\overline {AP}}}$ ${\displaystyle S_{1}}$ ${\displaystyle S_{2}}$ ${\displaystyle S_{1}A_{i}}$ ${\displaystyle S_{2}B_{i}}$

Note: The subdivisions can be continued beyond the points or in order to construct further points. However, since grinding cuts and a very uneven distribution of points then occur, it is better to transfer the construction of the above points symmetrically to the other parts of the hyperbola (see animation). ${\displaystyle A}$ ${\displaystyle B}$

Comment:

1. Steiner's generation is also available for ellipses and parabolas . In the parabolic case, the claim can easily be recalculated.
2. The Steiner generation is also called the parallelogram method, because instead of the vertices, other hyperbolic points on a hyperbolic diameter can also be used. Then a parallelogram appears instead of a rectangle.

Hyperbola as an affine image of the unit hyperbola

Hyperbola as an affine image of the unit hyperbola

Another definition of hyperbola uses a special geometric mapping, namely affinity . Here the hyperbola is defined as an affine image of the unit ${\displaystyle x^{2}-y^{2}=1}$ hyperbola .

Parametric representation

An affine mapping in the real plane has the form where is a regular matrix (determinant not 0) and is an arbitrary vector. If the column vectors are the matrix , then the unit hyperbola becomes the hyperbola ${\displaystyle {\vec {x}}\to {\vec {f}}_{0}+A{\vec {x}}}$ ${\displaystyle A}$ ${\displaystyle {\vec {f}}_{0}}$ ${\displaystyle {\vec {f}}_{1},{\vec {f}}_{2}}$ ${\displaystyle A}$ ${\displaystyle (\pm \cosh t,\sinh t),t\in \mathbb {R} ,}$

${\displaystyle {\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}\pm {\vec {f}}_{1}\cosh t+{\vec {f}}_{2}\sinh t}$

pictured. is the center point, a point of the hyperbola and tangent vector at this point. stand i. a. not perpendicular to each other. I.e. are i. A. not the vertex of the hyperbola. But are the direction vectors of the asymptotes. This definition of a hyperbola provides a simple parametric representation of any hyperbola. ${\displaystyle {\vec {f}}_{0}}$ ${\displaystyle {\vec {f}}_{0}+{\vec {f}}_{1}}$ ${\displaystyle {\vec {f}}_{2}}$ ${\displaystyle {\vec {f}}_{1},{\vec {f}}_{2}}$ ${\displaystyle {\vec {f}}_{0}\pm {\vec {f}}_{1}}$ ${\displaystyle {\vec {f}}_{1}\pm {\vec {f}}_{2}}$

Vertex, vertex shape

Since the tangent to the associated hyperbolic diameter is perpendicular in a vertex and the tangent direction is in a hyperbolic point

${\displaystyle {\vec {p}}'(t)={\vec {f}}_{1}\sinh t+{\vec {f}}_{2}\cosh t}$

the parameter of a vertex is given by the equation ${\displaystyle t_{0}}$

${\displaystyle {\vec {p}}'(t)\cdot ({\vec {p}}(t)-{\vec {f}}_{0})=({\vec {f}}_{1}\sinh t+{\vec {f}}_{2}\cosh t)\cdot ({\vec {f}}_{1}\cosh t+{\vec {f}}_{2}\sinh t)=0}$

and so off

${\displaystyle \coth(2t_{0})=-{\tfrac {{\vec {f}}_{1}^{\,2}+{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f}}_{2}}}}$

to

${\displaystyle t_{0}={\tfrac {1}{4}}\ln {\tfrac {({\vec {f}}_{1}-{\vec {f}}_{2})^{2}}{({\vec {f}}_{1}+{\vec {f}}_{2})^{2}}}.}$

The formulas were used. ${\displaystyle \cosh ^{2}x+\sinh ^{2}x=\cosh 2x,\ 2\sinh x\cosh x=\sinh 2x,\ \operatorname {arcoth} x={\tfrac {1}{2}}\ln {\tfrac {x+1}{x-1}}}$

If is, and the parametric representation is already in vertex form. ${\displaystyle {\vec {f}}_{1}\cdot {\vec {f}}_{2}=0}$ ${\displaystyle t_{0}=0}$

The two vertices of the hyperbola are ${\displaystyle {\vec {f}}_{0}\pm ({\vec {f}}_{1}\cosh t_{0}+{\vec {f}}_{2}\sinh t_{0}).}$

Out

${\displaystyle {\vec {x}}={\vec {p}}(t)={\vec {p}}(t-t_{0}+t_{0})={\vec {f}}_{0}\pm {\vec {f}}_{1}\cosh((t-t_{0})+t_{0})+{\vec {f}}_{2}\sinh((t-t_{0})+t_{0})}$

and the addition theorems for the hyperbolic functions result in the vertex shape of the parametric representation of the hyperbola:

${\displaystyle {\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}\pm ({\vec {f}}_{1}\cosh t_{0}+{\vec {f}}_{2}\sinh t_{0})\cosh(t-t_{0})+({\vec {f}}_{1}\sinh t_{0}+{\vec {f}}_{2}\cosh t_{0})\sinh(t-t_{0})}$

Examples

Hyperbola as a graph of the function y = 1 / x (example 3)

Hyperbola: transformation to vertex shape (example 5)

1. ${\displaystyle {\vec {f}}_{0}={\begin{pmatrix}0\\0\end{pmatrix}},\ {\vec {f}}_{1}={\begin{pmatrix}a\\0\end{pmatrix}},\ {\vec {f}}_{2}={\begin{pmatrix}0\\b\end{pmatrix}}}$ provides the usual parametric representation of the hyperbola with the equation ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1:\quad {\vec {x}}={\vec {p}}(t)={\begin{pmatrix}a\cosh t\\b\sinh t\end{pmatrix}}}$
2. ${\displaystyle {\vec {f}}_{0}={\begin{pmatrix}x_{0}\\y_{0}\end{pmatrix}},\ {\vec {f}}_{1}={\begin{pmatrix}a\cos \varphi \\a\sin \varphi \end{pmatrix}},\ {\vec {f}}_{2}={\begin{pmatrix}-b\sin \varphi \\b\cos \varphi \end{pmatrix}}}$provides the parametric representation of the hyperbola, which emerges from the hyperbola by rotating it by the angle and then shifting it by . The parametric representation is already in vertex form. That is, are the vertices of the hyperbola. ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$ ${\displaystyle \varphi }$ ${\displaystyle {\vec {f}}_{0}}$ ${\displaystyle {\vec {f}}_{0}\pm {\vec {f}}_{1}}$
3. ${\displaystyle {\vec {f}}_{0}={\begin{pmatrix}0\\0\end{pmatrix}},\ {\vec {f}}_{1}={\begin{pmatrix}1\\1\end{pmatrix}},\ {\vec {f}}_{2}={\begin{pmatrix}-1\\1\end{pmatrix}}}$yields the hyperbola with the equation When detecting one use ${\displaystyle y={\tfrac {1}{x}}.}$ ${\displaystyle xy=1}$ ${\displaystyle \cosh ^{2}t-\sinh ^{2}t=1.}$
4. If one depicts the hyperbola with affine mappings of the form , one obtains the family of all hyperbolas with asymptotes parallel to the axis. The center of such a hyperbola is The specialty of this hyperbola family is that they can be represented as function graphs. ${\displaystyle y={\tfrac {1}{x}}}$ ${\displaystyle (x,y)\to (x+x_{0},ay+y_{0}),a\neq 0}$ ${\displaystyle y={\tfrac {a}{x-x_{0}}}+y_{0}}$ ${\displaystyle (x_{0},y_{0}).}$
5. The parametric representation

${\displaystyle {\vec {x}}={\vec {p}}(t)=\pm {\begin{pmatrix}30\\0\end{pmatrix}}\cosh t+{\begin{pmatrix}-30\\3{\sqrt {5}}\end{pmatrix}}\sinh t}$a hyperbola is not in a vertex shape.

The vertex parameter results from to ${\displaystyle t_{0}={\tfrac {1}{4}}\ln {\tfrac {({\vec {f}}_{1}-{\vec {f}}_{2})^{2}}{({\vec {f}}_{1}+{\vec {f}}_{2})^{2}}}}$ ${\displaystyle t_{0}=\ln 3.}$

The vertex shape of the parametric plot is:

${\displaystyle {\vec {x}}={\vec {p}}(t)=\pm {\begin{pmatrix}\ 10\\4{\sqrt {5}}\end{pmatrix}}\cosh(t-\ln 3)+{\begin{pmatrix}-10\\5{\sqrt {5}}\end{pmatrix}}\sinh(t-\ln 3)}$

The parting is and ${\displaystyle (10,4{\sqrt {5}}),(-10,-4{\sqrt {5}})}$

the semi-axes ${\displaystyle a=6{\sqrt {5}},\ b=15.}$

implicit representation

Solving the parametric representation using Cramer's rule after and used , we obtain the implicit representation ${\displaystyle \;\cosh t,\;\sinh t\;}$ ${\displaystyle \;\cosh ^{2}t-\sinh ^{2}t-1=0\;}$

${\displaystyle \det({\vec {x}}\!-\!{\vec {f}}\!_{0},{\vec {f}}\!_{2})^{2}-\det({\vec {f}}\!_{1},{\vec {x}}\!-\!{\vec {f}}\!_{0})^{2}-\det({\vec {f}}\!_{1},{\vec {f}}\!_{2})^{2}=0}$.

Hyperbola in space

If the vectors are out of the , a parametric representation of a hyperbola in space is obtained. ${\displaystyle {\vec {f}}_{0},{\vec {f}}_{1},{\vec {f}}_{2}}$ ${\displaystyle \mathbb {R} ^{3}}$

Hyperbola as an affine image of the hyperbola y = 1 / x

Since the unit hyperbola is equivalent to the hyperbola (see above), any hyperbola can also be understood as an affine image of the hyperbola : ${\displaystyle x^{2}-y^{2}=1}$ ${\displaystyle y=1/x}$ ${\displaystyle y=1/x}$

${\displaystyle {\vec {x}}={\vec {p}}(t)={\vec {f}}_{0}+{\vec {f}}_{1}t+{\vec {f}}_{2}{\tfrac {1}{t}},\ t\neq 0}$

${\displaystyle M={\vec {f}}_{0}}$is the center of the hyperbola, pointing in the direction of the asymptotes and is a point of the hyperbola. ${\displaystyle {\vec {f}}_{1},{\vec {f}}_{2}}$ ${\displaystyle {\vec {f}}_{0}+{\vec {f}}_{1}+{\vec {f}}_{2}}$

For the tangent vector results

${\displaystyle {\vec {p}}'(t)={\vec {f}}_{1}-{\vec {f}}_{2}{\tfrac {1}{t^{2}}}.}$

In a vertex , the tangent to the associated hyperbolic diameter is perpendicular, i.e. h., it is

${\displaystyle {\vec {p}}'(t)\cdot ({\vec {p}}(t)-{\vec {f}}_{0})=({\vec {f}}_{1}-{\vec {f}}_{2}{\tfrac {1}{t^{2}}})\cdot ({\vec {f}}_{1}t+{\vec {f}}_{2}{\tfrac {1}{t}})={\vec {f}}_{1}^{2}t-{\vec {f}}_{2}^{2}{\tfrac {1}{t^{3}}}=0.}$

So is the vertex parameter

${\displaystyle t_{0}=\pm {\sqrt[{4}]{\frac {{\vec {f}}_{2}^{2}}{{\vec {f}}_{1}^{2}}}}.}$

For is and are the vertices of the hyperbola. ${\displaystyle |{\vec {f}}_{1}|=|{\vec {f}}_{2}|}$ ${\displaystyle t_{0}=\pm 1}$ ${\displaystyle {\vec {f}}_{0}\pm ({\vec {f}}_{1}+{\vec {f}}_{2})}$

Tangent construction

Tangent construction: Asymptotes and P given → tangent

The tangent vector can be written like this by factoring out: ${\displaystyle {\tfrac {1}{t}}}$

${\displaystyle {\vec {p}}'(t)={\tfrac {1}{t}}({\vec {f}}_{1}t-{\vec {f}}_{2}{\tfrac {1}{t}})}$

That means, in the parallelogram , the diagonal is parallel to the tangent in the hyperbolic point (see picture). This property provides an easy way to construct the tangent at a hyperbolic point. ${\displaystyle M={\vec {f}}_{0},A={\vec {f}}_{0}+{\vec {f}}_{1}t,B={\vec {f}}_{0}+{\vec {f}}_{2}{\tfrac {1}{t}},P={\vec {f}}_{0}+{\vec {f}}_{1}t+{\vec {f}}_{2}{\tfrac {1}{t}}}$ ${\displaystyle AB}$ ${\displaystyle P}$

Remark: This property of a hyperbola is an affine version of the 3-point degeneration of Pascal's theorem .

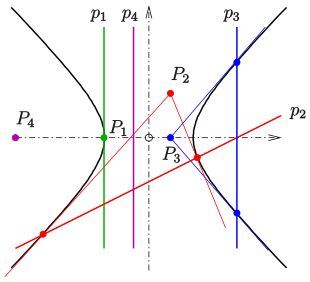
Point construction

Point construction: Asymptotes and P ₁ given → P ₂

Another property of a hyperbola allows the construction of hyperbola points if the asymptotes and a point of the hyperbola are known:

For a hyperbola with the parametric representation (the center point was assumed to be the zero point for the sake of simplicity): ${\displaystyle {\vec {x}}={\vec {p}}(t)={\vec {f}}_{1}t+{\vec {f}}_{2}{\tfrac {1}{t}}}$

If there are two hyperbolic points, the points lie ${\displaystyle P_{1}={\vec {f}}_{1}t_{1}+{\vec {f}}_{2}{\tfrac {1}{t_{1}}},\ P_{2}={\vec {f}}_{1}t_{2}+{\vec {f}}_{2}{\tfrac {1}{t_{2}}}}$

${\displaystyle A={\vec {a}}={\vec {f}}_{1}t_{2}+{\vec {f}}_{2}{\tfrac {1}{t_{1}}},\ B={\vec {b}}={\vec {f}}_{1}t_{1}+{\vec {f}}_{2}{\tfrac {1}{t_{2}}}}$

on a straight line through the center point (see picture). The simple proof follows from . ${\displaystyle {\tfrac {1}{t_{2}}}{\vec {a}}={\tfrac {1}{t_{1}}}{\vec {b}}}$

Note: This property of a hyperbola is an affine version of the 4-point degeneration of Pascal's theorem .

Tangent-asymptote triangle

Hyperbola: tangent-asymptote triangle

For the following considerations, for the sake of simplicity we assume that the center point is at the origin (0,0) and that the vectors have the same length. If the latter is not the case, the parametric representation is first brought into apex form (see above). As a result, the vertices and the minor vertices are. So is and . ${\displaystyle {\vec {f}}_{1},{\vec {f}}_{2}}$ ${\displaystyle \pm ({\vec {f}}_{1}+{\vec {f}}_{2})}$ ${\displaystyle \pm ({\vec {f}}_{1}-{\vec {f}}_{2})}$ ${\displaystyle |{\vec {f}}_{1}+{\vec {f}}_{2}|=a}$ ${\displaystyle |{\vec {f}}_{1}-{\vec {f}}_{2}|=b}$

If the points of intersection of the tangent in the hyperbolic point with the asymptotes are calculated, the two points are obtained ${\displaystyle {\vec {p}}(t_{0})={\vec {f}}_{1}t_{0}+{\vec {f}}_{2}{\tfrac {1}{t_{0}}}}$

${\displaystyle C=2t_{0}{\vec {f}}_{1},\ D={\tfrac {2}{t_{0}}}{\vec {f}}_{2}.}$

The area of ​​the triangle can be expressed using a 2 × 2 determinant: ${\displaystyle M,C,D}$

${\displaystyle F={\tfrac {1}{2}}|\det(2t_{0}{\vec {f}}_{1},{\tfrac {2}{t_{0}}}{\vec {f}}_{2})|=2|\det({\vec {f}}_{1},{\vec {f}}_{2})|}$

See rules of calculation for determinants . is the area of ​​the diamond spanned by. The area of ​​a diamond is equal to half of the diagonal product. The diagonals of this diamond are the semi-axes . So: ${\displaystyle |\det({\vec {f}}_{1},{\vec {f}}_{2})|}$ ${\displaystyle {\vec {f}}_{1},{\vec {f}}_{2}}$ ${\displaystyle a,b}$

The area of the triangle is independent of the hyperbola point ${\displaystyle M,C,D}$ ${\displaystyle F=ab.}$

Affine self-images of the hyperbola y = 1 / x

Not every affine mapping of the real affine plane (see previous section) maps the hyperbola onto another hyperbola. The following affine mappings leave the hyperbola invariant as a whole: ${\displaystyle y=1/x}$ ${\displaystyle y=1/x}$

• ${\displaystyle (x,y)\mapsto (ax,\textstyle {\frac {y}{a}}),\ a\neq 0}$
• ${\displaystyle (x,y)\mapsto (\textstyle {\frac {y}{m}},mx),\ m\neq 0}$

Special cases:

1. For every point of the plane remains fixed. This image is called identity. ${\displaystyle a=1}$
2. For each point of the hyperbola is moved, i.e. i.e. there is no fixed point on the hyperbola. ${\displaystyle a\neq 1}$
3. For the figure is the point reflection at the zero point. ${\displaystyle a=-1}$
4. For the figure is the "normal" reflection on the straight line . ${\displaystyle m=1}$ ${\displaystyle y=x}$
5. For the figure is the oblique reflection on the straight line in the direction of the straight line . (See section Centers of Parallel Chords .) ${\displaystyle m\neq 1}$ ${\displaystyle y=mx}$ ${\displaystyle y=-mx}$

Centers of parallel tendons

Hyperbola: The midpoints of parallel tendons lie on a straight line.

Hyperbola: The midpoint of a tendon also bisects the asymptote tendon.

The following applies to each hyperbola:

• The centers of parallel tendons (see picture) lie on a straight line through the center of the hyperbola.

That is, for each pair of points of a chord there is an oblique reflection on a straight line through the center of the hyperbola, which swaps the points and maps the hyperbola onto itself. An oblique mirroring is understood as a generalization of an ordinary mirroring on a straight line , in which all the points-to-image points are parallel to one another, but not necessarily perpendicular to the mirror axis . ${\displaystyle P,Q}$ ${\displaystyle s}$ ${\displaystyle P,Q}$ ${\displaystyle m}$ ${\displaystyle m}$

The easiest way to prove this property is at the hyperbola . Since all hyperbolas are affine images of the unit hyperbola and thus also of the hyperbola and, in the case of an affine mapping, the centers of lines pass into the centers of the image lines, the above property applies to all hyperbolas. ${\displaystyle y=1/x}$ ${\displaystyle y=1/x}$

Note: The points of the tendon may also lie on different branches of the hyperbola. ${\displaystyle s}$

A consequence of this symmetry is: The asymptotes of the hyperbola are interchanged in the oblique reflection and the midpoint of a hyperbolic chord also halves the corresponding distance between the asymptotes, i.e. i.e., it applies . This property can be used to construct any number of further hyperbolic points with known asymptotes and a point by using the respective segment to construct . ${\displaystyle M}$ ${\displaystyle PQ}$ ${\displaystyle {\overline {P}}\,{\overline {Q}}}$ ${\displaystyle |P{\overline {P}}|=|Q{\overline {Q}}|}$ ${\displaystyle P}$ ${\displaystyle Q}$ ${\displaystyle P{\overline {P}}}$ ${\displaystyle Q}$

If the chord degenerates into a tangent, the point of contact bisects the section between the asymptotes. ${\displaystyle PQ}$

Pole-polar relationship

Hyperbola: pole-polar relationship

A hyperbola can always be described in a suitable coordinate system by an equation of the form . The equation of the tangent in a hyperbolic point is If one allows in this equation that any point of the plane different from the zero point is, then the straight line is assigned to the point . This straight line does not go through the center of the hyperbola. ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$ ${\displaystyle P_{0}=(x_{0},y_{0})}$ ${\displaystyle {\tfrac {x_{0}x}{a^{2}}}-{\tfrac {y_{0}y}{b^{2}}}=1.}$ ${\displaystyle P_{0}=(x_{0},y_{0})}$ ${\displaystyle P_{0}=(x_{0},y_{0})\neq (0,0)}$ ${\displaystyle {\frac {x_{0}x}{a^{2}}}-{\frac {y_{0}y}{b^{2}}}=1}$

You can do the opposite

the straight line the point or ${\displaystyle y=mx+d,\ d\neq 0}$ ${\displaystyle \left(-{\frac {ma^{2}}{d}},-{\frac {b^{2}}{d}}\right)}$

the straight line the point ${\displaystyle x=c,\ c\neq 0}$ ${\displaystyle \left({\frac {a^{2}}{c}},0\right)}$

assign. Such an assignment point ↔ straight line is called a polarity or pole-polar relationship . The pole is the point, the polar is the corresponding straight line.

The meaning of this pole-polar relationship is that the possible intersections of the polar of a point with the hyperbola are the points of contact of the tangents through the pole to the hyperbola.

• If the point (pole) lies on the hyperbola, its polar is the tangent at this point (see picture:) . ${\displaystyle P_{1},\ p_{1}}$
• If the pole lies outside the hyperbola, the points of intersection of the polar with the hyperbola are the contact points of the tangents through the pole to the hyperbola (see picture:) . ${\displaystyle P_{2},\ p_{2},\ P_{3},\ p_{3}}$
• If the point lies within the hyperbola, its polar has no intersection with the hyperbola (see picture:) . ${\displaystyle P_{4},\ p_{4}}$

For proof: The determination of the intersection of the polar of a point with the hyperbola and the search for hyperbolic points whose tangents contain the point lead to the same system of equations. ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$ ${\displaystyle (x_{0},y_{0})}$

Remarks:

1. The point of intersection of two polars (e.g. in the picture:) is the pole of the straight line connecting the associated poles (here:) . ${\displaystyle p_{2},p_{3}}$ ${\displaystyle P_{2},P_{3}}$
2. The focal point or and the guideline or are polar to one another. ${\displaystyle (e,0)}$ ${\displaystyle (-e,0)}$ ${\displaystyle x={\tfrac {a^{2}}{e}}}$ ${\displaystyle x=-{\tfrac {a^{2}}{e}}}$
3. Straight lines through the center of the hyperbola have no poles. They say: "Your poles are on the long-distance straight ."
4. The center of the hyperbola has no polar, "it is the distant straight line".
5. Pole-polar relationships also exist for ellipses and parabolas . See also projective conic section .

Orthogonal tangents

Hyperbola with orthoptic curve (purple)

→ Main article : Orthoptic curve

For a hyperbola , the intersections of orthogonal tangents lie on the circle . (In the case there are no orthogonal tangents.) ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\,a>b}$ ${\displaystyle x^{2}+y^{2}=a^{2}-b^{2}}$ ${\displaystyle a\leq b}$

This circle is called the orthoptic curve of the given hyperbola.

Hyperbolas of the form y = a / (x − b) + c

Peripheral angle set for hyperbolas

Hyperbolas of the form are function graphs that are uniquely determined by the three parameters . So you need three points to determine these parameters. A quick method is based on the peripheral angle set for hyperbolas. ${\displaystyle y={\frac {a}{x-b}}+c}$ ${\displaystyle a,b,c}$

Hyperbola: set of peripheral angles

One angle to be measured between two chords, we carry two lines that are neither for - nor to the axis are parallel, a square one: ${\displaystyle x}$ ${\displaystyle y}$

For two lines we measure the corresponding angle with the number . ${\displaystyle y=m_{1}x+d_{1},\ y=m_{2}x+d_{2}\ ,m_{1},m_{2}\neq 0}$ ${\displaystyle {\frac {m_{1}}{m_{2}}}}$

Two straight lines are parallel if and thus the angular dimension is equal to 1. ${\displaystyle m_{1}=m_{2}}$

Analogous to the set of peripheral angles for circles, the applies here

Peripheral angle set (for hyperbolas):

For four points (see picture) the following applies: ${\displaystyle P_{i}=(x_{i},y_{i}),\ i=1,2,3,4,\ x_{i}\neq x_{k},y_{i}\neq y_{k},i\neq k}$

The four points only lie on a hyperbola of the shape if the angles at and in the above angle measure are equal, i.e. i.e. if: ${\displaystyle y={\tfrac {a}{x-b}}+c}$ ${\displaystyle P_{3}}$ ${\displaystyle P_{4}}$

${\displaystyle {\frac {(y_{4}-y_{1})}{(x_{4}-x_{1})}}{\frac {(x_{4}-x_{2})}{(y_{4}-y_{2})}}={\frac {(y_{3}-y_{1})}{(x_{3}-x_{1})}}{\frac {(x_{3}-x_{2})}{(y_{3}-y_{2})}}}$

(Proof by recalculation. One can assume for one direction that the points lie on a hyperbola y = a / x.)

3-point shape of a hyperbola

Analogous to the 2-point form of a straight line (slope angles are measured with the slope), the set of peripheral angles for hyperbolas results in

3-point form (for hyperbolas):

The equation of the hyperbola through three points is obtained by solving the equation ${\displaystyle P_{i}=(x_{i},y_{i}),\ i=1,2,3,\ x_{i}\neq x_{k},y_{i}\neq y_{k},i\neq k}$

${\displaystyle {\frac {({\color {red}y}-y_{1})}{({\color {green}x}-x_{1})}}{\frac {({\color {green}x}-x_{2})}{({\color {red}y}-y_{2})}}={\frac {(y_{3}-y_{1})}{(x_{3}-x_{1})}}{\frac {(x_{3}-x_{2})}{(y_{3}-y_{2})}}}$

after y.

Formula collection

Hyperbolic equation

A hyperbola with a center (0 | 0) and axis as the main axis satisfies the equation ${\displaystyle x}$

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1.}$

The asymptotes of the associated hyperbola are the straight lines:

${\displaystyle y=\pm {\frac {b}{a}}x.}$

Focal points are:

${\displaystyle (\pm ~{\sqrt {a^{2}+b^{2}}},0)}$

A hyperbola with a center and the straight line as the main axis satisfies the equation ${\displaystyle (x_{0}|y_{0})}$ ${\displaystyle y=y_{0}}$

${\displaystyle {\frac {(x-x_{0})^{2}}{a^{2}}}-{\frac {(y-y_{0})^{2}}{b^{2}}}=1.}$

Any hyperbola whose asymptotes are the straight lines with the equations has an equation of the form ${\displaystyle a_{1}x+b_{1}y=c_{1},\ a_{2}x+b_{2}y=c_{2}}$

${\displaystyle (a_{1}x+b_{1}y-c_{1})(a_{2}x+b_{2}y-c_{2})=c,\ c\neq 0.}$

E.g .: If the asymptotes are the coordinate axes , then all hyperbolas result from an equation . ${\displaystyle x=0,\ y=0}$ ${\displaystyle y=c/x}$

Vertex equation

Conic coulter

The family of hyperbolas, whose axis is the -axis, a vertex is the point (0,0) and the center (-a, 0), can be expressed by the equation ${\displaystyle x}$

${\displaystyle y^{2}=2px+(\varepsilon ^{2}-1)x^{2},\qquad p={\tfrac {b^{2}}{a}},\ \varepsilon ={\tfrac {e}{a}},\ e^{2}=a^{2}+b^{2}}$

describe.

The following applies to hyperbolas . Put in this equation ${\displaystyle 1<\varepsilon }$

${\displaystyle \varepsilon =0}$so you get a circle,

for an ellipse, ${\displaystyle 0<\varepsilon <1}$

for a parable. ${\displaystyle \varepsilon =1}$

With the same half parameter, the conic sections all have the same radius of curvature at the vertex S: ${\displaystyle p}$ ${\displaystyle \rho _{S}=p.}$

Parametric representations

for the hyperbola with the equation : ${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$

1: ${\displaystyle \left\{{\begin{matrix}x\,=\,\pm a\cosh t\\y\,=\,b\sinh t\end{matrix}}\right.\quad ,\ t\in \mathbb {R} .}$

2: ${\displaystyle \left\{{\begin{matrix}x\,=\,{\frac {a}{\cos t}}\\y\,=\,\pm b\tan t\end{matrix}}\right.\ ,\ 0\leq t<2\pi ;\;t\neq {\frac {\pi }{2}};\;t\neq {\frac {3}{2}}\pi }$

3: (Representation with rational functions). ${\displaystyle \left\{{\begin{matrix}x\,=\,\pm a\,{\tfrac {t^{2}+1}{2t}}\\y\,=\,b\,{\tfrac {t^{2}-1}{2t}}\end{matrix}}\right.\quad ,\ t>0}$

4: Tangent slope as a parameter:

A parametric representation that uses the tangent gradient in the respective hyperbolic point is obtained analogously to the case of the ellipse by replacing with and using formulas for the hyperbolic functions: ${\displaystyle m}$ ${\displaystyle b^{2}}$ ${\displaystyle -b^{2}}$

${\displaystyle {\vec {c}}_{\pm }(m)=\left(-{\frac {ma^{2}}{\pm {\sqrt {m^{2}a^{2}-b^{2}}}}}\;,\;{\frac {-b^{2}}{\pm {\sqrt {m^{2}a^{2}-b^{2}}}}}\right)\ ,\ |m|>b/a\ .}$

Here is the upper and the lower half of the hyperbola. The points with vertical tangents (vertices ) are not covered by this parametric representation. ${\displaystyle {\vec {c}}_{-}}$ ${\displaystyle {\vec {c}}_{+}}$ ${\displaystyle (\pm a,0)}$

The equation of the tangent in the point is ${\displaystyle {\vec {c}}_{\pm }(m)}$

${\displaystyle y=mx\pm {\sqrt {m^{2}a^{2}-b^{2}}}.}$

This equation is an essential tool in determining the orthoptic curve of a hyperbola.

In polar coordinates

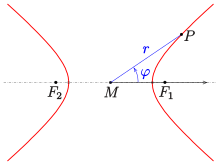
Hyperbola: polar representation, pole = center

Hyperbola: polar representation, pole = focal point

Note

1. in the first case (pole is the center of the hyperbola) that the radical edge can become negative. There are no hyperbolic points for such angles.
2. In the second case (pole is a focal point of the hyperbola) there are two hyperbolic points (because of ) on every ray for which the denominator is not 0 . For the two vertices result. ${\displaystyle \mp }$ ${\displaystyle \varphi =0}$

Angle to the main axis, pole in the center (0,0):

${\displaystyle r={\frac {b}{\sqrt {\varepsilon ^{2}\cos ^{2}\varphi -1}}},\quad \varepsilon ={\tfrac {e}{a}},\ e^{2}=a^{2}+b^{2}}$

Angle to the main axis, pole in a focal point (see conic section ):

${\displaystyle r={\frac {p}{1\mp \varepsilon \cos \varphi }},\quad p={\tfrac {b^{2}}{a}}}$

Tangent equation

Center point (0 | 0), main axis as -axis, contact point ${\displaystyle x}$ ${\displaystyle (x_{B}|y_{B})}$

${\displaystyle {\frac {x_{B}x}{a^{2}}}-{\frac {y_{B}y}{b^{2}}}=1}$

Center point , main axis parallel to the -axis, contact point ${\displaystyle (x_{0}|y_{0})}$ ${\displaystyle x}$ ${\displaystyle (x_{B}|y_{B})}$

${\displaystyle {\frac {(x_{B}-x_{0})(x-x_{0})}{a^{2}}}-{\frac {(y_{B}-y_{0})(y-y_{0})}{b^{2}}}=1}$

Radius of curvature

The radius of curvature of the hyperbola in the two vertices is ${\displaystyle {\tfrac {x^{2}}{a^{2}}}-{\tfrac {y^{2}}{b^{2}}}=1}$ ${\displaystyle (\pm a,0)}$

${\displaystyle \rho ={\frac {b^{2}}{a}}}$ (like an ellipse in the main vertices).

Hyperbola as Trisektrix

Already Pappos of Alexandria (4th century) used this property of the hyperbola as an additional aid to solve the problem of dividing an angle into three . It has been proven that there is no solution if you are limited to the “Euclidean tools”, compasses and rulers .

The method described below is largely taken from the essay On the Trisection of the Angle by K. Matter (1902). In the construction shown therein, in contrast to that according to Pappos , the angle vertex does not lie on the ordinate of the hyperbola. If the same chord length is always used for different angular widths, then with just one constructed hyperbola, the angular widths from approx. To close to three can be achieved if there is sufficient space . The names of the hyperbola have been adapted to the current standard. ${\displaystyle O,}$ ${\displaystyle s,}$ ${\displaystyle 20^{\circ }}$ ${\displaystyle 180^{\circ },}$ ${\displaystyle 0^{\circ },}$

Sketch for preliminary consideration

As a preliminary consideration z. B. before an angle as part of a circular sector in which the point divides the arc in proportion . A triangle with the chord drawn in it receives the angle at the vertex and the angle at the vertex, according to the set of circular angles. If the vertex is the coordinate origin of the Cartesian coordinate system , the coordinate (distance ) applies to the point ${\displaystyle {BOA}=\alpha }$ ${\displaystyle C}$ ${\displaystyle OBA}$ ${\displaystyle 2:1}$ ${\displaystyle ABC}$ ${\displaystyle {\overline {AB}}=s,}$ ${\displaystyle A}$ ${\displaystyle \varphi }$ ${\displaystyle B}$ ${\displaystyle 2\varphi .}$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle y}$ ${\displaystyle {\overline {CD}}}$

(1) ${\displaystyle y=x\cdot \tan(\varphi )=(s-x)\cdot \tan(2\varphi ),}$

Elimination of the ${\displaystyle \tan(\varphi ):}$

Transform terms of equation (1)

(2) ${\displaystyle \tan(\varphi )={\frac {y}{x}},}$

(3) is a double-angle function , therefore also applies ${\displaystyle \tan(2\varphi )={\frac {y}{s-x}}}$

(4) ${\displaystyle \tan(2\varphi )={\frac {2\tan(\varphi )}{1-\tan ^{2}(\varphi )}},}$

(2) insert in (4)

(5) ${\displaystyle \tan(2\varphi )={\frac {2{\frac {y}{x}}}{1-{\frac {y^{2}}{x^{2}}}}}=2{\frac {y}{x}}\cdot {\frac {x^{2}}{x^{2}-y^{2}}}={\frac {2yx}{x^{2}-y^{2}}},}$

Equate (5) and (3), quasi eliminate ${\displaystyle \tan(2\varphi )}$

(6) ${\displaystyle \tan(2\varphi )={\frac {2yx}{x^{2}-y^{2}}}={\frac {y}{s-x}}\Rightarrow \;\;{\frac {2x}{x^{2}-y^{2}}}={\frac {1}{s-x}}\Rightarrow \;\;2x\left(s-x\right)=x^{2}-y^{2},}$

thus holds for ${\displaystyle y^{2}}$

(7) ${\displaystyle y^{2}=x^{2}-2sx+2x^{2},}$

finally you get the hyperbola equation

${\displaystyle y^{2}=3x^{2}-2sx.}$

This results in design-relevant features that also apply without the use of the Cartesian coordinate system, i.e. H. a specific direction or position of the tendon is not required: ${\displaystyle s}$

the center point is on the tendon ${\displaystyle s,}$

the semi-axis ${\displaystyle a={\frac {s}{3}},}$

the eccentricity ${\displaystyle e=2\cdot {\frac {s}{3}},}$

the left hyperload runs through the vertex (hereinafter referred to as vertex ). ${\displaystyle A}$ ${\displaystyle S_{2}}$

Animation of the trisection of the angle using the hyperbola

The actual construction begins with the positioning of the angle vertex and the drawing in of the two angle legs, which enclose any angular width of the angle . Then an arc is drawn around with a freely selectable radius; the first focal point and the second vertex of the later hyperbola result at the angled legs. There follows a straight line through the points and the distance is almost the tendon after the tendon-thirds of the in and the distance is from straight line plotted on the, it will be apparent to the desired hyperbola the second focal point and the ${\displaystyle O}$ ${\displaystyle \alpha }$ ${\displaystyle O}$ ${\displaystyle F_{1}}$ ${\displaystyle S_{2}}$ ${\displaystyle F_{1}}$ ${\displaystyle S_{2}.}$ ${\displaystyle {\overline {F_{1}S_{2}}}}$ ${\displaystyle s.}$ ${\displaystyle s}$ ${\displaystyle S_{1}}$ ${\displaystyle M,}$ ${\displaystyle {\overline {MS_{2}}}}$ ${\displaystyle S_{2}}$ ${\displaystyle F_{2}}$

Semi-axis and the ${\displaystyle a={\frac {s}{3}}={\overline {S_{1}M}}}$

eccentricity ${\displaystyle e=2\cdot {\frac {s}{3}}={\overline {F_{1}M}}.}$

Now the hyperbola with the help of the focal points of the vertex and z. B. drawn in by means of dynamic geometry software (DGS) or a mechanical hyperbolic circle. ${\displaystyle F_{1},}$ ${\displaystyle F_{2},}$ ${\displaystyle S_{1}}$

The right branch of the hyperbola intersects the arc and provides the conclusion, it only needs a half-line starting by ${\displaystyle C}$ ${\displaystyle OF_{1}C}$ ${\displaystyle \angle {F_{1}OC}={\frac {\alpha }{3}}.}$ ${\displaystyle O}$ ${\displaystyle C.}$

Hyperbolas as plane sections of quadrics

The following second-order surfaces ( quadrics ) have hyperbolas as plane sections:

• Elliptical cone (see also conic section )
• Hyperbolic cylinder
• Hyperbolic paraboloid
• Single-shell hyperboloid
• Double-shell hyperboloid

• 

  Elliptical cone

• 

  Hyperbolic cylinder

• 

  Hyperbolic paraboloid

• 

  Single-shell hyperboloid

• 

  Double-shell hyperboloid

Hyperbola y = 1 / x over any number field

If one considers the set of points in an affine plane over any (commutative) body that satisfies the hyperbolic equation, many properties of the real case remain, which are formulated with "intersect", "connect" and "parallel" and whose proofs are only multiplication / Use division and addition / subtraction. E.g .: ${\displaystyle K}$ ${\displaystyle y=1/x}$

• A straight line intersects the hyperbola in at most two points. ${\displaystyle y={\tfrac {1}{x}}}$
• Through each Hyperbelpunkt there except the axis parallel lines exactly a straight line with the hyperbola only point in common, the tangent : . A straight line without an intersection is called a passer-by , a straight line with two intersections is called a secant . ${\displaystyle (x_{0},{\tfrac {1}{x_{0}}})}$ ${\displaystyle x=x_{0},\ y=1/x_{0}}$ ${\displaystyle (x_{0},{\tfrac {1}{x_{0}}})}$ ${\displaystyle y=-{\tfrac {1}{x_{0}^{2}}}x+{\tfrac {2}{x_{0}}}}$

Differences to the real case:

1. For (rational numbers) the straight line is a passerby, because the equation has no solution. ${\displaystyle K=\mathbb {Q} }$ ${\displaystyle y={\tfrac {1}{2}}x}$ ${\displaystyle x^{2}=2}$ ${\displaystyle \mathbb {Q} }$
2. There are no passers-by for (complex numbers). E.g .: intersects the hyperbola in the points . ${\displaystyle K=\mathbb {C} }$ ${\displaystyle y=-x}$ ${\displaystyle (i,-i),(-i,i)}$
3. If the body has characteristic 2 (i.e. 1 + 1 = 0), there are no secants among the straight lines , since every equation in the case of characteristic 2 has at most one solution (there is no “ ”). The tangent at the hyperbolic point has (for characteristic 2) the equation . That means, all tangents go through the zero point (0,0). ${\displaystyle y=mx,\ m\neq 0}$ ${\displaystyle x^{2}={\tfrac {1}{m}}}$ ${\displaystyle \pm }$ ${\displaystyle (x_{0},{\tfrac {1}{x_{0}}})}$ ${\displaystyle y={\tfrac {1}{x_{0}^{2}}}x}$

See also

• Confocal conic sections
• Hyperbolic Circle by Frans van Schooten
• Trisectricix

literature

• Peter Proff: The interpretation of the terms "ellipse", "parabola" and "hyperbola" according to Apollonios v. Perge. In: “gelêrter der arzeniê, ouch apotêker”. Contributions to the history of science. Festschrift for the 70th birthday of Willem F. Daems. Edited by Gundolf Keil , Horst Wellm Verlag, Pattensen / Hanover 1982 (= Würzburg medical-historical research, 24), ISBN 3-921456-35-5 , pp. 17–34.

Web links

• Eric W. Weisstein : Hyperbola . In: MathWorld (English).
• Thread construction of a hyperbola. Geogebra
• John J. O'Connor, Edmund F. Robertson :  Hyperbola. In: MacTutor History of Mathematics archive .
• Hyperbola calculations (JavaScript)
• Hyperbole. In: mathematische-basteleien.de. Retrieved February 9, 2015 . 
• Frans van Schooten: Mathematical Oeffeningen . 1659

Individual evidence

1. ^ IN Bronstein, KA Semendjajew (founder), Günter Grosche (editing), Eberhard Zeidler (ed.): Teubner-Taschenbuch der Mathematik. Teubner, Stuttgart 1996, ISBN 3-8154-2001-6 , p. 24.
2. ^ Frans van Schooten : Mathematische Oeffeningen , Leyden, 1659, p. 327
3. ↑ ^{a b} Erich Hartmann: Projective geometry. (PDF; 180 kB). Short script, TU Darmstadt, pp. 12-16.
4. ^ Jacob Steiner's lectures on synthetic geometry. BG Teubner, Leipzig 1867. Part 2, p. 96. ( limited preview in the Google book search)
5. ↑ Lecture Note Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF; 757 kB) p. 33.
6. ↑ Lecture Note Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF; 757 kB) p. 32.
7. ↑ ^{a b} Regina Bruischütz: 5th angular division into three with hyperbolas (according to Pappus approx. 300 AD). In: Angular three-part construction - construction with additional tools (Part A). University of Bayreuth, May 26, 1997, p. 3 , accessed on July 22, 2019 . 
8. ^ Robert C. Yates: THE TRISECTION PROBLEM, 3. The Hyperbola. In: ERIC. National Council of Teachers of Mathematics, Inc., Washington, DC, 1971, pp. 32-33 , accessed July 27, 2019 . 
9. ↑ K. Matter: To the trisection of the angle. In: e-perodica. ETH Zurich, 1902, pp. 20-23 , accessed on July 22, 2019 . 
10. ↑ CDKG: Computer-aided Descriptive and Constructive Geometry. (PDF; 3.4 MB) TU Darmstadt, p. 108.
11. ↑ CDKG: Computer-aided Descriptive and Constructive Geometry. (PDF; 3.4 MB) TU Darmstadt, p. 118.
12. ↑ CDKG: Computer-aided Descriptive and Constructive Geometry. (PDF; 3.4 MB) TU Darmstadt, p. 123.