Triangular face

general triangle

The exact calculation of the area of ​​a triangle is one of the oldest problems in geometry . As early as ancient Egypt, when the Nile floods receded, fertile farmland had to be redistributed. Triangles and their area calculation still form an important basis for land surveying today - irregular areas can be determined using triangulation . The principle of triangular networks is also used in modern areas of mathematics .

Your physical unit is the square meter (m²).

Area calculation on a flat triangle

Triangle areas are easy to calculate if you know the lengths of all three sides or the lengths of two sides and the angle they include.

Given all three side lengths

If all three side lengths of a triangle are known, Heron's theorem can be applied:

${\displaystyle F={\sqrt {s(s-a)(s-b)(s-c)}}}$

Here is half the circumference of the triangle. ${\displaystyle s={\tfrac {a+b+c}{2}}}$

Special case of an equilateral triangle

From follows for half the circumference . Inserting this into the above formula results in: ${\displaystyle a=b=c}$ ${\displaystyle s={\tfrac {3a}{2}}}$

${\displaystyle F={\sqrt {{\tfrac {3a}{2}}({\tfrac {a}{2}})({\tfrac {a}{2}})({\tfrac {a}{2}})}}={\tfrac {\sqrt {3}}{4}}a^{2}}$

Given two side lengths and included angles

Relationship between triangle and parallelogram .

If two side lengths (and the included angle ) of a triangle are known, the area of ​​the triangle can be determined in several ways. The general formula for the area of a triangle is ${\displaystyle F}$

${\displaystyle F={\frac {a\cdot h}{2}},}$

this is the basic page and the subsequent vertical standing height of the triangle. The formula provides half of the content of a parallelogram , because each triangle can be supplemented with a rotated copy of itself to form the corresponding parallelogram. Its surface area can be reduced to that of a rectangle by means of shear . Another approach arises because a triangle can always be seen as a special case of a trapezoid in which the second base side consists of only one point. ${\displaystyle a}$ ${\displaystyle h}$

Although each side of the triangle can be used as a base side, the calculation of the corresponding height is, however, except in special cases elementary geometrically impossible. From the trigonometry one concludes: . This results in: ${\displaystyle h\,(=h_{a})=b\cdot \sin {\gamma }}$

${\displaystyle F={\frac {ab\cdot \sin {\gamma }}{2}}.}$

Special cases

Right triangle

In the case of right triangles , the height coincides with one of the cathets .

In the case of right triangles , the height does not have to be calculated separately. If the length of the two cathets is known, it results . ${\displaystyle F={\tfrac {a\cdot b}{2}}}$

Isosceles triangle

The height of an isosceles triangle with the legs always cuts the base in the middle and can therefore be calculated using the Pythagorean theorem and is therefore ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle h={\sqrt {a^{2}-{\tfrac {b^{2}}{4}}}}}$

${\displaystyle F={\tfrac {b}{4}}{\sqrt {4a^{2}-b^{2}}}}$.

From the above Formula also results:

${\displaystyle F={\frac {1}{2}}{a^{2}}\cdot \sin {\gamma }.}$

Equilateral triangle

As a regular polygon , every equilateral triangle with the edge length has the height , from which the area results . ${\displaystyle a}$ ${\displaystyle h={\tfrac {a{\sqrt {3}}}{2}}}$ ${\displaystyle F={\tfrac {\sqrt {3}}{4}}a^{2}}$

Because the angles in the equilateral triangle are all of the same size, it follows from the above. Formula also:

${\displaystyle F={\frac {1}{2}}{a^{2}}\cdot \sin 60^{\circ }.}$

Other cases

If the triangle can be clearly identified , further angles or side lengths may have to be calculated until sufficient information is available for one of the above formulas.

Calculation with coordinates

In the plane

Derivation of the triangular area using trapezoids ${\displaystyle F=A_{1}+A_{2}-A_{3}}$

Triangular area calculated using the parallelepiped spanned by its side vectors. ${\displaystyle F={\tfrac {1}{2}}\left|\det \left({\begin{matrix}u_{x}&v_{x}\\u_{y}&v_{y}\end{matrix}}\right)\right|}$ ${\displaystyle ={\tfrac {1}{2}}|u_{x}v_{y}-u_{y}v_{x}|}$

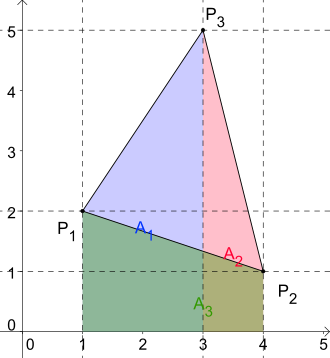
In the Euclidean plane with coordinate axes , the area for a triangle with points , and can be derived from the trapezoidal formula . When the triangle (possibly shifted to the first quadrant ) is projected onto one of the axes, three trapezoids result, the sum or difference of which is the area of ​​the triangle. All the required parameters can be read from the coordinates. For the area of ​​the triangle we get: ${\displaystyle P_{1}=(x_{1},y_{1})}$ ${\displaystyle P_{2}=(x_{2},y_{2})}$ ${\displaystyle P_{3}=(x_{3},y_{3})}$

${\displaystyle F={\tfrac {1}{2}}(y_{3}+y_{1})(x_{3}-x_{1})+{\tfrac {1}{2}}(y_{2}+y_{3})(x_{2}-x_{3})-{\tfrac {1}{2}}(y_{2}+y_{1})(x_{2}-x_{1})}$

${\displaystyle ={\tfrac {1}{2}}(x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2}))}$

This formula can be represented very clearly with the help of a determinant :

${\displaystyle F={\frac {1}{2}}\left|\det \left({\begin{matrix}1&x_{1}&y_{1}\\1&x_{2}&y_{2}\\1&x_{3}&y_{3}\end{matrix}}\right)\right|={\frac {1}{2}}\left|\det \left({\begin{matrix}1&1&1\\x_{1}&x_{2}&x_{3}\\y_{1}&y_{2}&y_{3}\end{matrix}}\right)\right|}$

If one shifts the triangle so that it lies on the zero point, then on the basis of Laplace's development theorem (development after the first column) results : ${\displaystyle P_{1}}$

${\displaystyle {\begin{aligned}F&={\frac {1}{2}}\left|\det \left({\begin{matrix}1&1&1\\0&x_{2}-x_{1}&x_{3}-x_{1}\\0&y_{2}-y_{1}&y_{3}-y_{1}\end{matrix}}\right)\right|\\&={\frac {1}{2}}\left|\det \left({\begin{matrix}x_{2}-x_{1}&x_{3}-x_{1}\\y_{2}-y_{1}&y_{3}-y_{1}\end{matrix}}\right)\right|\\&={\frac {1}{2}}|(x_{2}-x_{1})(y_{3}-y_{1})-(x_{3}-x_{1})(y_{2}-y_{1})|\end{aligned}}}$

This second representation in determinant form also results from the general volume formula for parallelepipeds , since a two-dimensional parallelepiped is a parallelogram with twice the triangular area. It is therefore necessary that the amount of the determinant of a - Matrix whose columns are the lateral vectors of a triangle, the dual area provides this triangle. The same approach is obtained if the triangular area is not understood as the sum of trapezoidal areas, but as the sum of three integrals over the linear functions that define the three sides. ${\displaystyle 2\times 2}$

It is also possible to represent the three sides as curves in the plane, then the triangle forms a piece-wise smooth closed curve, the enclosed area of ​​which can be calculated with the Leibniz sector formula .

In three-dimensional space

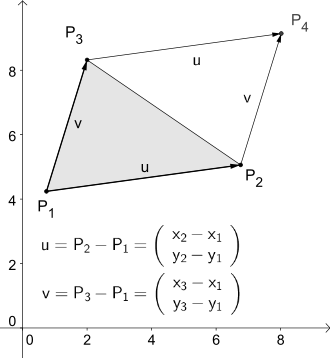
In Euclidean space the area of ​​the triangle that is spanned by and is obtained with the help of the cross product of the two vectors and . This yields a vector whose Euclidean norm is equal to the area of ​​the parallelogram spanned by and . ${\displaystyle (0,0,0),(x_{1},x_{2},x_{3})}$ ${\displaystyle (y_{1},y_{2},y_{3})}$ ${\displaystyle {\vec {x}}=(x_{1},x_{2},x_{3})}$ ${\displaystyle {\vec {y}}=(y_{1},y_{2},y_{3})}$ ${\displaystyle {\vec {x}}}$ ${\displaystyle {\vec {y}}}$

${\displaystyle 2F=\left|{\vec {x}}\times {\vec {y}}\right|=\left|{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\times {\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}\right|=\left|{\begin{pmatrix}x_{2}y_{3}-x_{3}y_{2}\\x_{3}y_{1}-x_{1}y_{3}\\x_{1}y_{2}-x_{2}y_{1}\end{pmatrix}}\right|={\sqrt {(x_{2}y_{3}-x_{3}y_{2})^{2}+(x_{3}y_{1}-x_{1}y_{3})^{2}+(x_{1}y_{2}-x_{2}y_{1})^{2}}}\,.}$

Or: With the help of the scalar product

${\displaystyle 2F={\sqrt {{\vec {x}}^{2}{\vec {y}}^{2}-({\vec {x}}\cdot {\vec {y}})^{2}}}}$.

Area calculation of spherical triangles

Strictly speaking, no triangle is flat on the earth's surface , as the earth is known to have an approximately spherical shape (see earth's curvature ). In the case of very large triangles (e.g. Cape Town - Rio de Janeiro - Tokyo) one therefore has to resort to methods of spherical geometry (or spherical trigonometry) or differential calculus :

According to Legendre's theorem , a small spherical triangle has almost the same area as a flat triangle with three sides of equal length. This so-called leveling becomes more precise the smaller the triangles become. This results in an iterative method of calculating the area of ​​a spherical triangle: Halve repeatedly the geodetic lines that form the boundary of the triangle and calculate the area sums resulting from the smaller triangles. The limit of this process exists and is the area of ​​the spherical triangle.

Of course, two direct ways lead to the goal more quickly: either via suitable formulas from spherical trigonometry or via the spherical excess (the excess of the angle sum over 180 °). For a spherical triangle with interior angles that lies on a sphere with a radius , the following formula applies: ${\displaystyle \alpha ,\beta ,\gamma }$ ${\displaystyle r}$

${\displaystyle F=(\alpha +\beta +\gamma -\pi )\cdot r^{2}}$

The excess is directly proportional to the area of ​​the triangle, which is precise enough on the earth's ellipsoid for the practice of geodesy . The replacement of spherical triangles with their flat equivalents becomes too imprecise from around 10 km.

literature

• Martin Nitschke: Geometry . Hanser Verlag, ISBN 3-446-22676-1 .

Web links

• Eric W. Weisstein : triangular area . In: MathWorld (English).