trigonometry

Illustrations of trigonometry in a book from 1687

The trigonometry ( Greek τρίγωνον trigonon , Triangle and μέτρον métron , measure ') is a branch of geometry and thus the math . As far as questions of planar geometry ( planimetry ) are treated trigonometrically, one speaks of planar trigonometry ; in addition, there is spherical trigonometry , which deals with spherical triangles (spherical triangles), and hyperbolic trigonometry . The following statements essentially relate to the field of plane trigonometry.

The basic task of trigonometry is to calculate other sizes of this triangle from three sizes of a given triangle (side lengths, angle sizes, lengths of triangle transversals, etc.). The trigonometric functions ( trigonometric functions , circular functions, goniometric functions) sine (sin), cos (cos) , tangent (tan), cotangent (cot) , secant (sec) and cosecant (csc) are used as aids . Trigonometric calculations can also refer to more complicated geometric objects, for example to polygons (polygons) , to problems of stereometry (spatial geometry) and to questions in many other areas (see below).

Trigonometry in the right triangle

Right triangle

The trigonometry of the right triangle is particularly simple . Since the sum of the angles of a triangle is 180 °, the right angle of such a triangle is the largest interior angle . The longest side (called the hypotenuse ) is opposite to it. The two shorter sides of the triangle are called cathets . When referring to one of the two smaller angle, it is useful to distinguish between the opposite side (the given angle with respect to) and the adjacent side (adjacent to the given angle) to distinguish. One now defines:

${\displaystyle {\begin{aligned}{\text{Sinus von }}\alpha &=\sin \alpha ={\frac {a}{c}}={\frac {\text{Gegenkathete}}{\text{Hypotenuse}}}\\[0.5ex]{\text{Kosinus von }}\alpha &=\cos \alpha ={\frac {b}{c}}={\frac {\text{Ankathete}}{\text{Hypotenuse}}}\\[0.5ex]{\text{Tangens von }}\alpha &=\tan \alpha ={\frac {a}{b}}={\frac {\text{Gegenkathete}}{\text{Ankathete}}}\\[0.5ex]{\text{Kotangens von }}\alpha &=\cot \alpha ={\frac {b}{a}}={\frac {\text{Ankathete}}{\text{Gegenkathete}}}\\[0.5ex]{\text{Sekans von }}\alpha &=\sec \alpha ={\frac {c}{b}}={\frac {\text{Hypotenuse}}{\text{Ankathete}}}\\[0.5ex]{\text{Kosekans von }}\alpha &=\csc \alpha ={\frac {c}{a}}={\frac {\text{Hypotenuse}}{\text{Gegenkathete}}}\end{aligned}}}$

These definitions make sense because different right triangles with the given angle are similar to each other , so they match in their aspect ratios. For example, one triangle could have sides twice as long as another. The fractions of the above definition equations would have the same values ​​in this case. These values ​​therefore only depend on the given angle. For this reason it makes sense to speak of functions of the angles.

Example: Calculating a side length

The following numerical values ​​are rounded off. The following quantities are given in a triangle ABC:

${\displaystyle b=5{,}5\,{\mbox{cm}};\quad \alpha =29^{\circ };\quad \gamma =90^{\circ }}$

The side length c is to be determined from this information. Since the adjacent side of is known and the hypotenuse is sought, the cosine function is used. ${\displaystyle \alpha }$

${\displaystyle \cos \alpha ={\frac {b}{c}}}$

${\displaystyle c={\frac {b}{\cos \alpha }}={\frac {5{,}5\,{\mbox{cm}}}{\cos 29^{\circ }}}=6{,}3\,{\mbox{cm}}}$

Example: Calculating an angle size

We know of a triangle ABC:

${\displaystyle a=3{,}1\,{\mbox{cm}};\quad b=5{,}5\,{\mbox{cm}};\quad \gamma =90^{\circ }}$

The angle is sought . The two given sides and are the adjacent and opposite sides of . Therefore it makes sense to use the tangent function. ${\displaystyle \beta }$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \beta }$

${\displaystyle \tan \beta ={\frac {b}{a}}={\frac {5{,}5\,{\mbox{cm}}}{3{,}1\,{\mbox{cm}}}}=1{,}8}$

While in the last example the cosine value had to be calculated for a known angle, the situation is reversed here. The associated angle is to be determined from a known tangent value. This requires the inverse function of the tangent function, the so-called arctangent function (arctan) or a set of tables from which the angle and the associated tangent value can be read. This gives:

${\displaystyle \beta =61{,}0^{\circ }}$

Definition of the trigonometric functions on the unit circle

Unit circle

All trigonometric functions of the angle θ can be constructed geometrically in the unit circle with center O.

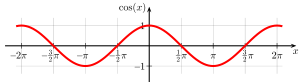
The definitions used so far can only be used for angles below 90 °. For many purposes, however, one is interested in trigonometric values ​​of larger angles. The unit circle , that is a circle with radius 1, allows such an extension of the previous definition. For the given angle, the corresponding point on the unit circle is determined. The x-coordinate of this point is the cosine value of the given angle, the y-coordinate is the sine value.

The definition of sine and cosine values ​​given above using the x and y coordinates can easily be extended to angles over 90 °. It can be seen that for angles between 90 ° and 270 ° the x-coordinate and thus also the cosine is negative, correspondingly for angles between 180 ° and 360 ° the y-coordinate and thus also the sine. The definition can also be easily transferred to angles greater than 360 ° and negative angles.

Note that in the modern approach the relationship between angle and sine or cosine is used to define the angle. The sine and cosine functions themselves are introduced via their series representation .

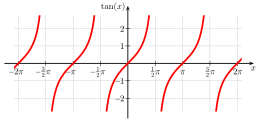
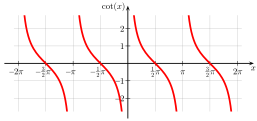
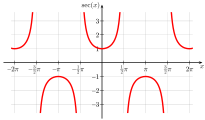
The other four trigonometric functions are defined by:

${\displaystyle \tan \alpha ={\frac {\sin \alpha }{\cos \alpha }}}$

${\displaystyle \cot \alpha ={\frac {1}{\tan \alpha }}={\frac {\cos \alpha }{\sin \alpha }}}$

${\displaystyle \sec \alpha ={\frac {1}{\cos \alpha }}}$

${\displaystyle \csc \alpha ={\frac {1}{\sin \alpha }}}$

• Graphs of the main trigonometric functions (angles in radians, i.e. π ≙ 180 °)
• 

  Sine

• 

  cosine

• 

  tangent

• 

  cotangent

• 

  Secans

• 

  cosecant

Trigonometry in the general triangle

For general triangles, too, a number of formulas have been developed that allow unknown side lengths or angle sizes to be determined. The law of sines and the law of cosines should be mentioned here in particular . Using the Law of Sines

${\displaystyle {\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}}$

is useful when either two sides and one of the two opposite angles or one side and two angles of a triangle are known. The law of cosines

${\displaystyle a^{2}\,=\,b^{2}+c^{2}-2bc\cos \alpha }$

${\displaystyle b^{2}\,=\,a^{2}+c^{2}-2ac\cos \beta }$

${\displaystyle c^{2}\,=\,a^{2}+b^{2}-2ab\cos \gamma }$

makes it possible to calculate the angles either from three given sides or the opposite side from two sides and their intermediate angle. Further formulas that apply to any triangle are the tangent theorem , the half-angle theorem (cotangent theorem) and Mollweid's formulas .

Properties and formulas

The articles on the six trigonometric functions ( sine , cosine , tangent , cotangent , secans , kosecans ) and the trigonometry formula collection contain numerous properties of these functions and formulas for calculating with them. The complementary formulas for sine and cosine are used particularly frequently

${\displaystyle \sin(90^{\circ }-\alpha )\,=\,\cos \alpha }$

${\displaystyle \cos(90^{\circ }-\alpha )\,=\,\sin \alpha }$

as well as the " trigonometric Pythagoras "

${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha \,=1}$

The addition theorems of the trigonometric functions and the conclusions drawn from them are also important . It is about trigonometric values ​​of sums or differences of angles. For example, for everyone and : ${\displaystyle \alpha }$ ${\displaystyle \beta }$

${\displaystyle \sin(\alpha \pm \beta )=\sin \alpha \cdot \cos \beta \pm \cos \alpha \cdot \sin \beta }$

${\displaystyle \cos(\alpha \pm \beta )=\cos \alpha \cdot \cos \beta \mp \sin \alpha \cdot \sin \beta }$

${\displaystyle \cos \alpha +\cos \beta =2\cos {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}}$

${\displaystyle \cos \alpha -\cos \beta =-2\sin {\frac {\alpha +\beta }{2}}\sin {\frac {\alpha -\beta }{2}}}$

${\displaystyle \sin \alpha +\sin \beta =2\sin {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}}$

${\displaystyle \sin \alpha -\sin \beta =2\cos {\frac {\alpha +\beta }{2}}\sin {\frac {\alpha -\beta }{2}}}$

Further identities can be found in the trigonometry formula collection .

application areas

Historical illustration of the measurement of a site with the help of a triangle (1667)

Trigonometry plays a crucial role in many areas:

In geodesy (surveying) one speaks of triangulation when one aims at other points from points of known position (angle measurement) and trigonometrically determines the positions of the new points. In astronomy , the distances to planets, moons and nearby fixed stars can be determined in a corresponding manner. The importance of trigonometry for the navigation of aircraft and ships and for spherical astronomy , in particular for the calculation of star and planetary positions, is just as important .

In physics , sine and cosine functions are used to describe vibrations and waves mathematically. The same applies to the time course of electrical voltage and electrical current strength in alternating current technology .

history

There were precursors to trigonometry in Greek mathematics as long ago as antiquity . Aristarchus of Samos used the properties of right triangles to calculate the distance between the earth and the sun or moon. It is known from the astronomers Hipparchus and Ptolemy that they worked with tendon tables, i.e. with tables for converting central angles (central angles) into chord lengths and vice versa. The values ​​of such tables are directly related to the sine function: The length of a circular chord results from the circle radius and the center angle according to ${\displaystyle r}$ ${\displaystyle \alpha }$

${\displaystyle s=2r\sin {\frac {\alpha }{2}}.}$

Similar tables have also been used in Indian mathematics . Arab scientists took over the results of Greeks and Indians and expanded trigonometry, especially spherical trigonometry. In medieval Europe , the knowledge of Arabic trigonometry was only known late. The first systematic representation of the area took place in the 15th century. In the age of the Renaissance , the increasing problems of ballistics and ocean shipping required an improvement in trigonometry and the trigonometric table . The German astronomer and mathematician Regiomontanus (Johann Müller) summarized theories and methods of plane and spherical trigonometry in the five-volume work De triangulis omnimodis . Because of this application, apart from sine and cosine, other angle functions were also used, such as sine versus = 1 - cos.

The term trigonometry was introduced by Bartholomäus Pitiscus in his Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus from 1595.

Most of the notation used today and the analytical representation of the trigonometric functions originate from Leonhard Euler .

literature

• Theophil Lambacher, Wilhelm Schweizer (ed.): Level trigonometry, mathematical teaching work for higher schools. Ernst Klett Verlag, Stuttgart, 1958.
• Heinz Pester, Wolfgang Pauli: Textbook and exercise book mathematics . 21st edition. Volume II. Planimetry, stereometry and trigonometry of the plane . Fachbuchverlag, Leipzig 1991, ISBN 978-3-446-00755-0 .

Web links

Wiktionary: Trigonometry  - explanations of meanings, word origins, synonyms, translations

Wikibooks: Mathematics: School Mathematics: Trigonometry  - Learning and Teaching Materials

• Help for trigonometry Dynamic documents for understanding the trigonometric functions
• Summary trigonometry for high school. State education server Baden-Württemberg
• Simple trigonometric equations, sample problems with solution tips. State education server Baden-Württemberg
• Trigonometric Java applets
• Trigonometry for students in the online math book
• On the history of trigonometry
• Trigonometric functions