triangle

This article covers the geometric concept of triangle; for further meanings see triangle (disambiguation) .

general triangle

A triangle (outdated also triangle , Latin: triangulum) is a polygon and a geometric figure . Within Euclidean geometry, it is the simplest figure in the plane , which is bounded by straight lines . Its boundary lines are called sides . In its interior, there are three clamp -angle , the so-called interior angles on. The vertices of these angles are called the corner points of the triangle. A generalization of the triangle concept to non-Euclidean geometries is also possible. In this case the boundary lines must be geodesic .

In trigonometry , a branch of mathematics , triangles play the essential role. See in particular triangle geometry .

Classification

Classification of the triangles:
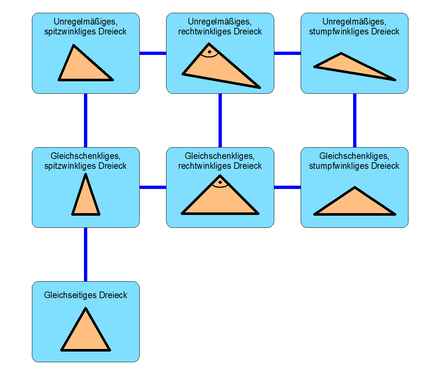
From left to right: acute-angled, right-angled , obtuse-angled.
From top to bottom: irregular, isosceles , equilateral

According to side lengths

• Irregular triangle
• Isosceles triangle
• Equilateral triangle

According to angles

• Acute triangle
• Right triangle
• Obtuse triangle

Acute and obtuse triangles are also grouped under the name oblique triangle .

The general triangle

Definition and characteristics

Triangle with its corners , sides and angles as well as the circumference , inscribed circle and part of a circle in the usual form

The sum of the interior angles in a flat triangle is always 180 °.

A triangle is defined by three points that are not on a straight line . They are called the corners of the triangle. The connecting lines between two corners are called sides of the triangle. The triangle divides the plane into two areas, the outside and the inside of the triangle. The angle formed by two sides that meet at a corner point is an important variable for characterizing the triangle.

In geometry , the corner points of the triangle are usually denoted by , and , usually as shown, counterclockwise . The side that is opposite to a corner, analog , or called. This z. B. the side opposite the corner point , so connects the points and . Often, with , and instead the length of the respective side , or denotes. The angles are called , and . the angle is at the corner point , is at the corner point and is at the corner point ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle a}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle BC}$ ${\displaystyle CA}$ ${\displaystyle AB}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle \alpha }$ ${\displaystyle A}$ ${\displaystyle \beta }$ ${\displaystyle B}$ ${\displaystyle \gamma }$ ${\displaystyle C}$

• The sum of the interior angles in a planar (flat) triangle is always 180 °.
• The sum of the outer angles is accordingly 360 °. Only one exterior angle is added to the total for each corner point. Since the two outer angles of a corner point are vertex angles , they are always the same size. Strictly speaking, the sum of all exterior angles is therefore 2 · 360 ° = 720 °.
• The total length of two sides of a triangle is at least as great as the length of the third side. These relationships can be expressed in what is known as the triangle inequality .

These intuitively understandable properties of plane triangles follow from the axioms of Euclidean geometry .

Excellent circles, straight lines and points

→ Main articles : Circles on the triangle  and Distinguished points in the triangle

Every triangle has a perimeter , that is, a circle that runs through its three corner points. The center of the circumference is the intersection of the three perpendiculars . These are the straight lines through the midpoints of the sides.

The bisectors of the three interior angles also intersect at a common point, namely in the center of the inscribed circle . This touches the three sides from the inside. The three circles that touch one side from the outside and the extensions of the other two sides are called circles of the triangle.

The center of gravity of a triangle is the common point of intersection of the three side bisectors , i.e. the respective connecting lines of the corner points with the center of the opposite side. The center of gravity divides the bisector in a ratio of 2: 1.

The three heights , i.e. the perpendiculars of the corner points on the opposite side, also intersect at a common point, the height intersection . With the help of the heights, the area of a triangle can be calculated (see triangle area ).

Euler's straight line e (black),
height intersection point H (red),
center of gravity S (green, intersection point of the side bisectors ),
circumcenter U (blue, intersection point of vertical lines ),
Feuerbach circle with center point N (black)

Another well-known circle on the triangle is the Feuerbach circle . It is also called the nine-point circle because it runs through the three side centers, the three base points of the heights and the three centers of the upper height sections. Its center, like the center of gravity, the center of the circumference and the intersection of the height, lies on Euler's straight line .

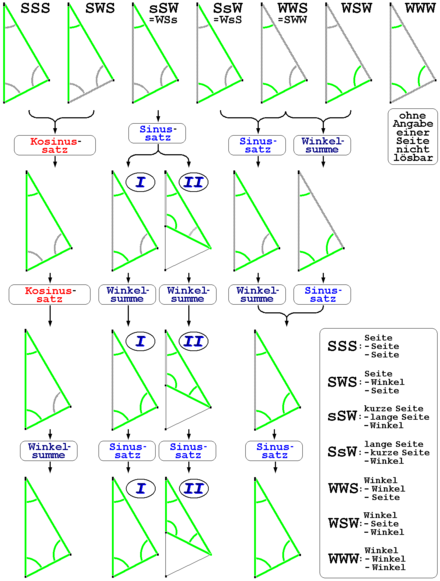
Calculation of any triangle

Overview of the calculation methods and tools to be used when calculating any triangle

A triangle has three sides and three interior angles . If there are three pieces of information about the size of these sides or angles , the remaining sides or angles can be calculated from them, unless only the three angles are given.

Depending on which combination of known sides and / or angles is given in detail, the result is either unambiguous or ambiguous (see adjacent figure).

The congruence theorems provide three constellations that can always be solved clearly, symbolically denoted by SSS , SWS and WSW , where S stands for a known side and W for a known angle.

SSW or WSS case

The SSW or WSS case, on the other hand, is only unambiguous if the known angle is opposite the larger of the two given sides (SsW case) - if it is opposite the smaller side (sSW case), there are usually two different triangles, the meet the initial conditions. However, this does not always have to be the case, as the special case with the aspect ratio 1: 2 and the angle 30 ° shows, in which there is nevertheless only one specific triangle if the angle to the longer side is 90 °. Finally, the purely computationally possible situation should be mentioned that no triangle at all fulfills the initial conditions, namely when the sine of the angle opposite the longer side results in a value> 1 (for real triangles, however, this case is naturally excluded).

WWS or SWW case

The WWS or SWW case can be solved in two ways (as can be seen in the adjacent figure): Either you first calculate one of the two missing sides using the sine theorem and then continue to calculate as in the SSW case , or you determine What is much more convenient is to use the sum of angles in the triangle to find the third angle that is still missing and then proceed as in the WSW case .

SSS case

If the largest of the three sides is smaller than the sum of the two other sides, then the triangle is uniquely determined (except for congruence). Otherwise there is no triangle with the given three sides. The interior angles of the triangle can be z. B. calculate with the cosine law.

WWW case

The WWW case cannot be solved unambiguously at all for plane triangles, because in this case there are actually only two pieces of information that are independent of each other, whereas the size of the third angle always results from the size of the other two. Without a given side, the shape of the triangle we are looking for is given, but its size remains undetermined.

Sine law and cosine law

The most important tools for calculating any triangle are, in addition to the sum of angles in the triangle, the sine and cosine theorem , compared to which the other triangular theorems such as the projection theorem, the tangent theorem and the half-angle theorem only play a subordinate role.

The most computationally complex, but also the most powerful of the three tools is the cosine theorem , as it is the only one that can be used to calculate a first angle for a triangle without any angle specifications (and then use the simpler sine law and the sum of angles in the triangle to help you). Accordingly, in the context discussed here, the cosine law is only used at the beginning of the calculation of a triangle of the type SSS or SWS , while everything else is done more easily and quickly using the sine law and the sum of angles.

As can be seen below, the cosine law begins just like the Pythagorean theorem , and in fact it can be viewed as a special case of the cosine law:

${\displaystyle a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot \cos(\alpha ),}$

${\displaystyle b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot \cos(\beta ),}$

${\displaystyle c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos(\gamma ).}$

If the angle enclosed by two given sides of a triangle becomes a right angle, its cosine becomes zero, and what is then left of the relevant cosine law is nothing more than another version of "Pythagoras".

If you only know its three sides of a triangle , and , its interior angles can be determined with the help of the arccosine function (arccos) as follows: ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

${\displaystyle {\begin{aligned}\cos(\alpha )&={\frac {b^{2}+c^{2}-a^{2}}{2\cdot b\cdot c}}\\\alpha &=\arccos \left({\frac {b^{2}+c^{2}-a^{2}}{2\cdot b\cdot c}}\right),\end{aligned}}}$

${\displaystyle {\begin{aligned}\cos(\beta )&={\frac {a^{2}+c^{2}-b^{2}}{2\cdot a\cdot c}}\\\beta &=\arccos \left({\frac {a^{2}+c^{2}-b^{2}}{2\cdot a\cdot c}}\right),\end{aligned}}}$

${\displaystyle {\begin{aligned}\cos(\gamma )&={\frac {a^{2}+b^{2}-c^{2}}{2\cdot a\cdot b}}\\\gamma &=\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2\cdot a\cdot b}}\right).\end{aligned}}}$

The sine law is available in three variants, which can be summarized as follows:

${\displaystyle {\frac {a}{\sin(\alpha )}}={\frac {b}{\sin(\beta )}}={\frac {c}{\sin(\gamma )}}=2\cdot r}$( Circumference diameter )

As you can see, the sine law is mathematically much less complicated: If you know one of the three fractions, you automatically know all the others. For this, however, at least one of the three interior angles must always be known and, if not, the cosine law must first be used (see above).

Formulas

Mathematical formulas for the general triangle
Area (see Heron's theorem )	${\displaystyle A={\frac {a\cdot h_{a}}{2}}={\frac {b\cdot h_{b}}{2}}={\frac {c\cdot h_{c}}{2}}}$
	${\displaystyle A={\sqrt {s\cdot (s-a)\cdot (s-b)\cdot (s-c)}};\;\;s={\frac {U}{2}}}$
scope	${\displaystyle U=a+b+c=8\cdot r\cdot \cos \left({\frac {\alpha }{2}}\right)\cdot \cos \left({\frac {\beta }{2}}\right)\cdot \cos \left({\frac {\gamma }{2}}\right)}$
Height from the lengths of the sides (using Heron's theorem)	${\displaystyle h_{a}={\frac {2\cdot {\sqrt {s\cdot (s-a)\cdot (s-b)\cdot (s-c)}}}{a}}}$
	${\displaystyle h_{b}={\frac {2\cdot {\sqrt {s\cdot (s-a)\cdot (s-b)\cdot (s-c)}}}{b}}}$
	${\displaystyle h_{c}={\frac {2\cdot {\sqrt {s\cdot (s-a)\cdot (s-b)\cdot (s-c)}}}{c}}}$
height	${\displaystyle h_{a}=c\cdot \sin(\beta )=b\cdot \sin(\gamma )}$
	${\displaystyle h_{b}=a\cdot \sin(\gamma )=c\cdot \sin(\alpha )}$
	${\displaystyle h_{c}=b\cdot \sin(\alpha )=a\cdot \sin(\beta )}$
Inscribed radius	${\displaystyle \rho =4\cdot r\cdot \sin \left({\frac {\alpha }{2}}\right)\cdot \sin \left({\frac {\beta }{2}}\right)\cdot \sin \left({\frac {\gamma }{2}}\right)={\frac {2\cdot A}{U}}}$
Perimeter radius	${\displaystyle r={\frac {a}{2\cdot \sin(\alpha )}}={\frac {b}{2\cdot \sin(\beta )}}={\frac {c}{2\cdot \sin(\gamma )}}={\frac {a\cdot b\cdot c}{4\cdot A}}}$
Length of the bisector	${\displaystyle w_{a}={\frac {1}{b+c}}\cdot {\sqrt {b\cdot c\cdot (a^{2}+b^{2}+c^{2})}}}$
	${\displaystyle w_{b}={\frac {1}{c+a}}\cdot {\sqrt {c\cdot a\cdot (a^{2}+b^{2}+c^{2})}}}$
	${\displaystyle w_{c}={\frac {1}{a+b}}\cdot {\sqrt {a\cdot b\cdot (a^{2}+b^{2}+c^{2})}}}$
Length of the side bisector	${\displaystyle s_{a}={\frac {1}{2}}\cdot {\sqrt {2\cdot b^{2}+2\cdot c^{2}-a^{2}}}}$
	${\displaystyle s_{b}={\frac {1}{2}}\cdot {\sqrt {2\cdot c^{2}+2\cdot a^{2}-b^{2}}}}$
	${\displaystyle s_{c}={\frac {1}{2}}\cdot {\sqrt {2\cdot a^{2}+2\cdot b^{2}-c^{2}}}}$
Inscribed center ${\displaystyle \;I}$ ( barycentric coordinates )	${\displaystyle (a,b,c)}$
Circumcenter ${\displaystyle \;U}$ (barycentric coordinates)	${\displaystyle {\begin{aligned}&(a^{2}\cdot (-a^{2}+b^{2}+c^{2}),\\&b^{2}\cdot (a^{2}-b^{2}+c^{2}),\\&c^{2}\cdot (a^{2}+b^{2}-c^{2}))\end{aligned}}}$
Height intersection ${\displaystyle \;H}$ (barycentric coordinates)	${\displaystyle {\begin{aligned}&((a^{2}-b^{2}+c^{2})\cdot (a^{2}+b^{2}-c^{2}),\\&(a^{2}+b^{2}-c^{2})\cdot (-a^{2}+b^{2}+c^{2}),\\&(-a^{2}+b^{2}+c^{2})\cdot (a^{2}-b^{2}+c^{2}))\end{aligned}}}$
Geometric focus ${\displaystyle \;S}$	${\displaystyle x_{s}={\frac {1}{3}}\cdot (x_{A}+x_{B}+x_{C})}$
	${\displaystyle y_{s}={\frac {1}{3}}\cdot (y_{A}+y_{B}+y_{C})}$

Special triangles

Equilateral triangles

An equilateral triangle .
The following applies: and ${\displaystyle a=b=c}$ ${\displaystyle \alpha =\beta =\gamma }$

→ Main article : Equilateral triangle

properties

A triangle in which all three sides are the same length is called an equilateral triangle . All three interior angles are the same size and are therefore 60 ° (it is therefore an acute triangle). The equilateral triangles thus belong to the regular polygons .

All equilateral triangles are similar to each other and congruent if and only if their side lengths are equal. The perpendicular , bisector and height to one side as well as bisector of the opposite angle coincide in an equilateral triangle. The same applies to the circumferential center , the inscribed center , the center of gravity and the vertical intersection of the equilateral triangle, so that this point is often simply called the center .

Formulas

Equilateral triangle with circumference and incircle

For an equilateral triangle with the side length : ${\displaystyle a}$

Area	${\displaystyle A={\frac {a^{2}}{4}}\cdot {\sqrt {3}}\,}$
scope	${\displaystyle U=3\cdot a}$
height	${\displaystyle h={\frac {a}{2}}\cdot {\sqrt {3}}=r_{u}+r_{i}}$
Inscribed radius	${\displaystyle \rho ={\frac {a}{6}}\cdot {\sqrt {3}}}$
Perimeter radius	${\displaystyle r={\frac {a}{3}}\cdot {\sqrt {3}}}$

For proof see web links below.

Isosceles triangles

An isosceles triangle .
The following applies: and ${\displaystyle a=b}$ ${\displaystyle \alpha =\beta }$

→ Main article : Isosceles triangle

An isosceles triangle is, according to modern understanding, a triangle with at least two sides of the same length. These sides are called the legs , the third side is called the base of the isosceles triangle. The two angles at the base ( base angle ) are equal. The point at which the two legs meet, will peak , called the angle of local is the angle at the tip .

A set square is a ruler in the shape of a right-angled isosceles triangle.

In an isosceles triangle, the median line of the base, the bisector of the base and the height on the base as well as the bisector of the apex angle coincide. One can determine the length of this distance, in particular the height , by applying the Pythagorean theorem to one half of the triangle. It turns out . ${\displaystyle h_{c}}$ ${\displaystyle h_{c}={\sqrt {a^{2}-{\tfrac {c^{2}}{4}}}}}$

Right triangles

→ Main article : Right triangle

Right triangle with the right angle at point C.

A right triangle is a triangle that has a 90 ° angle , i.e. a right angle . The side opposite the right angle is the longest side of the triangle and is called the hypotenuse . The other two sides are called cathets . In relation to one of the acute angles of the triangle, the cathetus adjacent to the angle is called the adjacent cathetus and the cathetus opposite the angle is called the opposite cathetus .

The lengths of the three sides of a right triangle are related by the Pythagorean Theorem : the square of the length of the hypotenuse ( denoted as in the graph ) is equal to the sum of the squares of the lengths of the cathets ( and ). Conversely, a triangle in which the lengths of the sides are related is a right-angled triangle with a hypotenuse . ${\displaystyle c}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a^{2}+b^{2}=c^{2}}$ ${\displaystyle c}$

The height of a right triangle shares the hypotenuse in two parts and so that the two sub-triangles with sides , , and , , in turn, are perpendicular. With knowledge of two of the six data ( , , , , and ) can be the missing four other values from those listed in the table below formulas to calculate. ${\displaystyle h=h_{c}}$ ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle p}$ ${\displaystyle a}$ ${\displaystyle h}$ ${\displaystyle q}$ ${\displaystyle h}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle h}$

Pythagorean theorem	${\displaystyle c^{2}=a^{2}+b^{2}}$
Set of cathets from Euclid	${\displaystyle a^{2}=c\cdot p}$
	${\displaystyle b^{2}=c\cdot q}$
Euclid's theorem of elevation	${\displaystyle h^{2}=p\cdot q}$

Trigonometric functions in a right triangle

The two acute angles of the right triangle can also be clearly determined through the relationship between the cathetus and the hypotenuse . The following six functions are trigonometric functions or trigonometric functions called.

→ Main article : Trigonometric function

function	calculation
The sine of the angle is defined as the ratio between the opposite cathetus (here:) and the hypotenuse (here:) . ${\displaystyle \alpha }$ ${\displaystyle a}$ ${\displaystyle c}$	${\displaystyle \sin(\alpha )={\frac {a}{c}}}$
The cosine of the angle is the ratio between the adjacent (here:) and the hypotenuse (here:) . ${\displaystyle \alpha }$ ${\displaystyle b}$ ${\displaystyle c}$	${\displaystyle \cos(\alpha )={\frac {b}{c}}}$
The tangent is given by the ratio between the opposite side and the adjacent side.	${\displaystyle \tan(\alpha )={\frac {a}{b}}}$

From the above, the following can be represented by reciprocating .

function	calculation
The cotangent is the ratio between the adjacent and the opposite side, i.e. the reciprocal of the tangent .	${\displaystyle \cot(\alpha )={\frac {b}{a}}={\frac {1}{\tan(\alpha )}}}$
The secant is the ratio of the hypotenuse to the adjacent, i.e. the reciprocal of the cosine .	${\displaystyle \sec(\alpha )={\frac {c}{b}}={\frac {1}{\cos(\alpha )}}}$
The cosecan is the ratio of the hypotenuse to the opposite cathetus, i.e. the reciprocal of the sine .	${\displaystyle \csc(\alpha )={\frac {c}{a}}={\frac {1}{\sin(\alpha )}}}$

The inverse functions of the mentioned trigonometric functions are called arcsine , arccosine , arctangent etc. - their main application is accordingly to supply the corresponding angles for given sine, cosine or tangent values.

Irregular triangles

A triangle is called irregular if it fulfills these two conditions:

• All three sides are of different lengths.
• All three angles are of different sizes.

If one of the two conditions is met, the other is automatically met.

Triangles of non-Euclidean geometry

Spherical triangles

Spherical triangle ( spherical triangle )

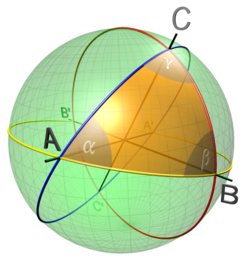
→ Main article: spherical triangle

Triangles on a sphere whose three sides are parts of great circles are called spherical triangles or spherical triangles. Their side lengths are not specified in the dimension of a length (meters, centimeters, etc.), but as the corresponding angle in the center of the sphere.

A spherical triangle has a sum of angles greater than 180 °. The "excess" is called spherical excess and is usually referred to in formulas as: ${\displaystyle \varepsilon }$

${\displaystyle \alpha +\beta +\gamma =180^{\circ }+\varepsilon }$.

The maximum excess of 360 ° occurs with a "triangle" with three angles stretched to 180 °. This triangle, which has degenerated into a great circle, has the sum of the angles 3 · 180 ° = 540 ° and . ${\displaystyle \varepsilon =540^{\circ }-180^{\circ }=360^{\circ }}$

The excess is directly related to the area of the triangle: ${\displaystyle F}$

${\displaystyle \varepsilon ={\frac {F}{R^{2}}}}$, or in degrees , ${\displaystyle \displaystyle \varepsilon ={\frac {180^{\circ }\cdot F}{\pi \cdot R^{2}}}}$

where means the radius of the sphere and the number of circles . ${\displaystyle R}$ ${\displaystyle \pi }$

Spherical triangles can be calculated in the same way as plane triangles, for which geodesy z. B. the spherical sine law, the cosine law, the projection law and various half-angle theorems - see spherical trigonometry .

Hyperbolic triangles

Saddle surface and geodesic triangle

The non-Euclidean geometry - in which the axiom of parallels does not apply - also includes triangles on a saddle surface . While a sphere is convexly curved everywhere , saddle and other hyperbolic surfaces have both convex and concave curvature (their product, the measure of curvature, is negative ).

Correspondingly, the excess is also negative - i.e. H. the sum of the angles of a triangle on a saddle surface is less than 180 °. The congruence theorems make statements about the triangle sizes (side length, angle ), which are necessary to clearly define a triangle.

Sentences around the triangle

• Similarity theorems
• Congruence clauses
• Pythagorean theorem
• Heron's theorem
• Thales theorem
• Stewart's Theorem
• Routh's theorem
• Circles at the triangle : circumference , incircle , arrival circle , Feuerbach circle
• Euler's straight line
• Samson straight line
• Symmedians and Lemoine point
• Fermat point
• Elevation base triangle
• Morley triangle
• Napoleon triangle and Napoleon point
• Pedoe's inequality
• Trigonometry formula collection

Triangle as a symbol

→ Main article : Triangle (symbol)

The triangle is used as a symbol, for example in theology, as an ideological symbol, as a mathematical symbol and also in signs.

See also

• Support triangle - auxiliary triangle for determining a true length in the descriptive geometry
• Pascal's triangle - number pyramid made of binomial coefficients
• Penrose triangle ( "Tribar" ) - an optical illusion
• Reuleaux triangle - the simplest, non-trivial example of an equal thickness
• Sierpiński triangle - a fractal
• Kobon triangles - made up of intersecting straight lines
• Characteristic triangle of differential calculus
• Triangulation , trilateration - method for determining position
• Barycentric coordinates: Barycentric coordinates in triangular geometry
• Tübingen triangle for modeling quasicrystals

literature

• Max Koecher , Aloys Krieg : level geometry . 3. Edition. Springer, Berlin 2007, ISBN 978-3-540-49327-3 , pp. 71-91, 108-135, 143-197 .
• Joseph von Radowitz: The formulas of geometry and trigonometry . Ferdinand Dümmler, Berlin 1827 ( limited preview in the Google book search).

Web links

Wikiquote: Triangle  Quotes

Commons : Triangles  - collection of images, videos and audio files

Wiktionary: triangle  - explanations of meanings, word origins, synonyms, translations

Wikibooks: Mathematics: School Mathematics: Trigonometry  - Learning and Teaching Materials

Wikibooks: triangle construction  - learning and teaching materials

• Eric W. Weisstein : Triangle . In: MathWorld (English).
• Steve Phelps: A Tour of Triangle Geometry

Individual evidence