Regular polygon

Regular polygons

A regular polygon , regular polygon , regular polygon , regular polygon or isogon (from Greek ἴσος , equal and γωνία , angle) is a planar polygon in geometry that is both equilateral and equiangular . In the case of a regular polygon, all sides are therefore of the same length and all interior angles are the same size. The corners of a regular polygon all lie on a common virtual or real circle , with neighboring corners appearing at the same central angle.

Regular polygons can be simple or flipped . Simple regular polygons are always convex . Overturned regular polygons are called regular star polygons . The symmetry group of a regular corner is the dihedral group , consisting of precisely rotations and reflections . ${\displaystyle n}$ ${\displaystyle D_{n}}$ ${\displaystyle n}$ ${\displaystyle n}$

All parameters of regular polygons, such as the length of the diagonals, the circumference or the area, can be specified with the help of trigonometric functions . However, not all regular polygons can be constructed with a compass and ruler . Regular polygons are used, among other things, to approximate the number of circles , for tiling , in architecture and as a coin shape . ${\displaystyle \pi }$

definition

A polygon with the sides and the interior angles is called regular if ${\displaystyle n}$ ${\displaystyle a,b,c,\ldots }$ ${\displaystyle \alpha ,\beta ,\gamma ,\ldots }$

${\displaystyle a=b=c=\dotsb }$   and   ${\displaystyle \alpha =\beta =\gamma =\dotsb }$

applies. In a regular polygon, all sides are therefore congruent to one another and all angles are the same size.

classification

Names of regular polygons and other star shapes

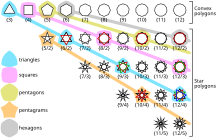
A distinction is made between simple and overlapped regular polygons. All simple regular polygons with the same number of corners are similar to one another and are denoted by the Schläfli symbol in combinatorial geometry . In order to rule out degenerate cases, it is usually assumed. The first simple regular polygons are: ${\displaystyle \{n\}}$ ${\displaystyle n\geq 3}$

• the equilateral triangle , ${\displaystyle \{3\}}$
• the square , ${\displaystyle \{4\}}$
• the regular pentagon and ${\displaystyle \{5\}}$
• the regular hexagon . ${\displaystyle \{6\}}$

Overturned regular polygons are called regular star polygons and have a greater variety of shapes. They are identified by the Schläfli symbol , with the number of revolutions of the polygon around its center. The circulation rate has to prime to be, otherwise degenerate polygon. The first regular star polygons are ${\displaystyle \{n/m\}}$ ${\displaystyle 2\leq m<n/2}$ ${\displaystyle n}$

• the five-star , ${\displaystyle \{5/2\}}$
• the seven stars and as well ${\displaystyle \{7/2\}}$ ${\displaystyle \{7/3\}}$
• the eight star . ${\displaystyle \{8/3\}}$

The number of different types of regular polygons with corners is thus , where is Euler's phi function . Are and are not coprime, the Schläfli symbol is used to designate stars that are composed of several regular polygons. Examples are the hexagram and the octagram . ${\displaystyle n}$ ${\displaystyle {\tfrac {1}{2}}\varphi (n)}$ ${\displaystyle \varphi }$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle \{n/m\}}$ ${\displaystyle \{6/2\}}$ ${\displaystyle \{8/2\}}$

Parameters

angle

Sizes in the regular hexagon

The corners of a regular polygon lie concyclically on a common circle. A regular polygon is thus a polygonal chord and thus has a perimeter with a perimeter radius . In addition, the corners are equidistant on the circle, i.e. corners lying next to each other appear at the same central angle (central angle) ${\displaystyle r_{u}}$

${\displaystyle \mu ={\frac {1}{n}}\cdot 360^{\circ }={\frac {2\pi }{n}}}$.

A regular polygon is thus also a tangent polygon with an inscribed circle with an inscribed circle radius . The inscribed circle touches the polygon sides in the side centers. The inscribed center of the circle coincides with the center of the circumference and is called the center of the polygon. Since the sum of the angles in a simple corner always results, measure all interior angles in a simple regular polygon ${\displaystyle r_{i}}$ ${\displaystyle n}$ ${\displaystyle (n-2)\cdot 180^{\circ }}$

${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }=\pi -{\frac {2\pi }{n}}}$.

As at the corners of a polygon interior and exterior angles to supplement all exterior angles are equal in a simple regular polygon and measure each ${\displaystyle 180^{\circ }}$

${\displaystyle \alpha '={\frac {1}{n}}\cdot 360^{\circ }={\frac {2\pi }{n}}}$.

For example, the following values ​​result for the angles in regular polygons:

Polygon	Center angle ${\displaystyle \mu }$		Interior angle ${\displaystyle \alpha }$		Exterior angle ${\displaystyle \alpha '}$
	Degree	Radians	Degree	Radians	Degree	Radians
triangle	${\displaystyle 120^{\circ }}$	${\displaystyle {\tfrac {2}{3}}\pi }$	${\displaystyle 60^{\circ }}$	${\displaystyle {\tfrac {1}{3}}\pi }$	${\displaystyle 120^{\circ }}$	${\displaystyle {\tfrac {2}{3}}\pi }$
square	${\displaystyle 90^{\circ }}$	${\displaystyle {\tfrac {1}{2}}\pi }$	${\displaystyle 90^{\circ }}$	${\displaystyle {\tfrac {1}{2}}\pi }$	${\displaystyle 90^{\circ }}$	${\displaystyle {\tfrac {1}{2}}\pi }$
pentagon	${\displaystyle 72^{\circ }}$	${\displaystyle {\tfrac {2}{5}}\pi }$	${\displaystyle 108^{\circ }}$	${\displaystyle {\tfrac {3}{5}}\pi }$	${\displaystyle 72^{\circ }}$	${\displaystyle {\tfrac {2}{5}}\pi }$
hexagon	${\displaystyle 60^{\circ }}$	${\displaystyle {\tfrac {1}{3}}\pi }$	${\displaystyle 120^{\circ }}$	${\displaystyle {\tfrac {2}{3}}\pi }$	${\displaystyle 60^{\circ }}$	${\displaystyle {\tfrac {1}{3}}\pi }$
octagon	${\displaystyle 45^{\circ }}$	${\displaystyle {\tfrac {1}{4}}\pi }$	${\displaystyle 135^{\circ }}$	${\displaystyle {\tfrac {3}{4}}\pi }$	${\displaystyle 45^{\circ }}$	${\displaystyle {\tfrac {1}{4}}\pi }$
decagon	${\displaystyle 36^{\circ }}$	${\displaystyle {\tfrac {1}{5}}\pi }$	${\displaystyle 144^{\circ }}$	${\displaystyle {\tfrac {4}{5}}\pi }$	${\displaystyle 36^{\circ }}$	${\displaystyle {\tfrac {1}{5}}\pi }$
Dodecagon	${\displaystyle 30^{\circ }}$	${\displaystyle {\tfrac {1}{6}}\pi }$	${\displaystyle 150^{\circ }}$	${\displaystyle {\tfrac {5}{6}}\pi }$	${\displaystyle 30^{\circ }}$	${\displaystyle {\tfrac {1}{6}}\pi }$

Lengths

Determination triangle

The most important parameters of simple regular polygons can be determined with the help of the determination triangle which is formed by the center point and two adjacent corners of the polygon. The determination triangle is isosceles with the apex angle , the base angles , the legs , the base and the height . If the determination triangle is divided into two right-angled triangles along the height (the apothema ), the following relationships result between the side length , the circumferential radius and the trigonometric functions ( sine and cosine , tangent and cotangent as well as secant and cosecant ) with the center angle given above the incircle radius : ${\displaystyle \mu }$ ${\displaystyle {\tfrac {\alpha }{2}}}$ ${\displaystyle r_{u}}$ ${\displaystyle a}$ ${\displaystyle r_{i}}$ ${\displaystyle a}$ ${\displaystyle r_{u}}$ ${\displaystyle r_{i}}$

${\displaystyle a=2\,r_{u}\cdot \sin \left({\frac {\pi }{n}}\right)=2\,r_{i}\cdot \tan \left({\frac {\pi }{n}}\right)}$

${\displaystyle r_{u}={\frac {a}{2}}\cdot \csc \left({\frac {\pi }{n}}\right)=r_{i}\cdot \sec \left({\frac {\pi }{n}}\right)}$

${\displaystyle r_{i}={\frac {a}{2}}\cdot \cot \left({\frac {\pi }{n}}\right)=r_{u}\cdot \cos \left({\frac {\pi }{n}}\right)}$

For some values ​​of , explicit formulas for the function values ​​of the trigonometric functions (see the Trigonometry formula collection ) and thus for the lengths in simple regular polygons can be specified, for example: ${\displaystyle n}$

Polygon	Side length given ${\displaystyle a}$		Given radius ${\displaystyle r_{u}}$		Inscribed radius given ${\displaystyle r_{i}}$
	Perimeter radius	Inscribed radius	Side length	Inscribed radius	Side length	Perimeter radius
triangle	${\displaystyle a\cdot {\tfrac {1}{3}}{\sqrt {3}}}$	${\displaystyle a\cdot {\tfrac {1}{6}}{\sqrt {3}}}$	${\displaystyle r_{u}\cdot {\sqrt {3}}}$	${\displaystyle r_{u}\cdot {\tfrac {1}{2}}}$	${\displaystyle r_{i}\cdot 2{\sqrt {3}}}$	${\displaystyle r_{i}\cdot 2}$
square	${\displaystyle a\cdot {\tfrac {1}{2}}{\sqrt {2}}}$	${\displaystyle a\cdot {\tfrac {1}{2}}}$	${\displaystyle r_{u}\cdot {\sqrt {2}}}$	${\displaystyle r_{u}\cdot {\tfrac {1}{2}}{\sqrt {2}}}$	${\displaystyle r_{i}\cdot 2}$	${\displaystyle r_{i}\cdot {\sqrt {2}}}$
pentagon	${\displaystyle a\cdot {\sqrt {{\tfrac {1}{10}}\left(5+{\sqrt {5}}\right)}}}$	${\displaystyle a\cdot {\tfrac {1}{2}}{\sqrt {{\tfrac {1}{5}}\left(5+2{\sqrt {5}}\right)}}}$	${\displaystyle r_{u}\cdot {\sqrt {{\tfrac {1}{2}}\left(5-{\sqrt {5}}\right)}}}$	${\displaystyle r_{u}\cdot {\tfrac {1}{4}}\left(1+{\sqrt {5}}\right)}$	${\displaystyle r_{i}\cdot 2{\sqrt {5-2{\sqrt {5}}}}}$	${\displaystyle r_{i}\cdot \left({\sqrt {5}}-1\right)}$
hexagon	${\displaystyle a\cdot 1}$	${\displaystyle a\cdot {\tfrac {1}{2}}{\sqrt {3}}}$	${\displaystyle r_{u}\cdot 1}$	${\displaystyle r_{u}\cdot {\tfrac {1}{2}}{\sqrt {3}}}$	${\displaystyle r_{i}\cdot {\tfrac {2}{3}}{\sqrt {3}}}$	${\displaystyle r_{i}\cdot {\tfrac {2}{3}}{\sqrt {3}}}$
octagon	${\displaystyle a\cdot {\sqrt {{\tfrac {1}{2}}\left(2+{\sqrt {2}}\right)}}}$	${\displaystyle a\cdot {\tfrac {1}{2}}\left(1+{\sqrt {2}}\right)}$	${\displaystyle r_{u}\cdot {\sqrt {2-{\sqrt {2}}}}}$	${\displaystyle r_{u}\cdot {\tfrac {1}{2}}{\sqrt {2+{\sqrt {2}}}}}$	${\displaystyle r_{i}\cdot 2\left({\sqrt {2}}-1\right)}$	${\displaystyle r_{i}\cdot {\sqrt {2\left(2-{\sqrt {2}}\right)}}}$
decagon	${\displaystyle a\cdot {\tfrac {1}{2}}\left(1+{\sqrt {5}}\right)}$	${\displaystyle a\cdot {\tfrac {1}{2}}{\sqrt {5+2{\sqrt {5}}}}}$	${\displaystyle r_{u}\cdot {\tfrac {1}{2}}\left({\sqrt {5}}-1\right)}$	${\displaystyle r_{u}\cdot {\tfrac {1}{2}}{\sqrt {{\tfrac {1}{2}}\left(5+{\sqrt {5}}\right)}}}$	${\displaystyle r_{i}\cdot 2{\sqrt {{\tfrac {1}{5}}\left(5-2{\sqrt {5}}\right)}}}$	${\displaystyle r_{i}\cdot {\sqrt {{\tfrac {2}{5}}\left(5-{\sqrt {5}}\right)}}}$
Dodecagon	${\displaystyle a\cdot {\sqrt {2+{\sqrt {3}}}}}$	${\displaystyle a\cdot {\tfrac {1}{2}}\left(2+{\sqrt {3}}\right)}$	${\displaystyle r_{u}\cdot {\sqrt {2-{\sqrt {3}}}}}$	${\displaystyle r_{u}\cdot {\tfrac {1}{2}}{\sqrt {2+{\sqrt {3}}}}}$	${\displaystyle r_{i}\cdot 2\left(2-{\sqrt {3}}\right)}$	${\displaystyle r_{i}\cdot 2{\sqrt {2-{\sqrt {3}}}}}$

Perimeter and area

The circumference of a simple regular polygon is times the length of the side and therefore ${\displaystyle n}$

${\displaystyle U=n\,a=2\,n\,r_{u}\cdot \sin \left({\frac {\pi }{n}}\right)=2\,n\,r_{i}\cdot \tan \left({\frac {\pi }{n}}\right)}$.

The area of a simple regular polygon is correspondingly times the area of ​​the determination triangle : ${\displaystyle n}$

${\displaystyle A={\frac {n\,a\,r_{i}}{2}}={\frac {n\,a^{2}}{4}}\cdot \cot \left({\frac {\pi }{n}}\right)=n\,r_{i}^{2}\cdot \tan \left({\frac {\pi }{n}}\right)={\frac {n\,r_{u}^{2}}{2}}\cdot \sin \left({\frac {2\pi }{n}}\right)}$.

The last equation follows from the double angle formula . This results, for example, in the following explicit formulas for the perimeter and area of ​​simple regular polygons:

Polygon	Side length given ${\displaystyle a}$		Given radius ${\displaystyle r_{u}}$		Inscribed radius given ${\displaystyle r_{i}}$
	scope	Area	scope	Area	scope	Area
triangle	${\displaystyle a\cdot 3}$	${\displaystyle a^{2}\cdot {\tfrac {1}{4}}{\sqrt {3}}}$	${\displaystyle r_{u}\cdot 3{\sqrt {3}}}$	${\displaystyle r_{u}^{2}\cdot {\tfrac {3}{4}}{\sqrt {3}}}$	${\displaystyle r_{i}\cdot 6{\sqrt {3}}}$	${\displaystyle r_{i}^{2}\cdot 3{\sqrt {3}}}$
square	${\displaystyle a\cdot 4}$	${\displaystyle a^{2}\cdot 1}$	${\displaystyle r_{u}\cdot 4{\sqrt {2}}}$	${\displaystyle r_{u}^{2}\cdot 2}$	${\displaystyle r_{i}\cdot 8}$	${\displaystyle r_{i}^{2}\cdot 4}$
pentagon	${\displaystyle a\cdot 5}$	${\displaystyle a^{2}\cdot {\tfrac {1}{4}}{\sqrt {5\left(5+2{\sqrt {5}}\right)}}}$	${\displaystyle r_{u}\cdot 5{\sqrt {{\tfrac {1}{2}}\left(5-{\sqrt {5}}\right)}}}$	${\displaystyle r_{u}^{2}\cdot {\tfrac {5}{4}}{\sqrt {{\tfrac {1}{2}}\left(5+{\sqrt {5}}\right)}}}$	${\displaystyle r_{i}\cdot 10{\sqrt {5-2{\sqrt {5}}}}}$	${\displaystyle r_{i}^{2}\cdot 5{\sqrt {5-2{\sqrt {5}}}}}$
hexagon	${\displaystyle a\cdot 6}$	${\displaystyle a^{2}\cdot {\tfrac {3}{2}}{\sqrt {3}}}$	${\displaystyle r_{u}\cdot 6}$	${\displaystyle r_{u}^{2}\cdot {\tfrac {3}{2}}{\sqrt {3}}}$	${\displaystyle r_{i}\cdot 4{\sqrt {3}}}$	${\displaystyle r_{i}^{2}\cdot 2{\sqrt {3}}}$
octagon	${\displaystyle a\cdot 8}$	${\displaystyle a^{2}\cdot 2\left(1+{\sqrt {2}}\right)}$	${\displaystyle r_{u}\cdot 8{\sqrt {2-{\sqrt {2}}}}}$	${\displaystyle r_{u}^{2}\cdot 2{\sqrt {2}}}$	${\displaystyle r_{i}\cdot 16\left({\sqrt {2}}-1\right)}$	${\displaystyle r_{i}^{2}\cdot 8\left({\sqrt {2}}-1\right)}$
decagon	${\displaystyle a\cdot 10}$	${\displaystyle a^{2}\cdot {\tfrac {5}{2}}{\sqrt {5+2{\sqrt {5}}}}}$	${\displaystyle r_{u}\cdot 5\left({\sqrt {5}}-1\right)}$	${\displaystyle r_{u}^{2}\cdot {\tfrac {5}{2}}{\sqrt {{\tfrac {1}{2}}\left(5-{\sqrt {5}}\right)}}}$	${\displaystyle r_{i}\cdot 4{\sqrt {5\left(5-2{\sqrt {5}}\right)}}}$	${\displaystyle r_{i}^{2}\cdot 2{\sqrt {5\left(5-2{\sqrt {5}}\right)}}}$
Dodecagon	${\displaystyle a\cdot 12}$	${\displaystyle a^{2}\cdot 3\left(2+{\sqrt {3}}\right)}$	${\displaystyle r_{u}\cdot 12{\sqrt {2-{\sqrt {3}}}}}$	${\displaystyle r_{u}^{2}\cdot 3}$	${\displaystyle r_{i}\cdot 24\left(2-{\sqrt {3}}\right)}$	${\displaystyle r_{i}^{2}\cdot 12\left(2-{\sqrt {3}}\right)}$

Diagonals

Diagonals in a regular octagon

Diagonals to extend from every corner of a regular corner . The length of the diagonals can in turn be determined with the help of the determination triangle that is formed by the center of the polygon and the two end points of the diagonal. The determination triangle of the -th diagonal,, is again isosceles and has the legs , the base and the apex angle . This results in the length of the -th diagonal ${\displaystyle n}$ ${\displaystyle n-3}$ ${\displaystyle d_{1}}$ ${\displaystyle d_{n-3}}$ ${\displaystyle k}$ ${\displaystyle k=1,\dotsc ,n-3}$ ${\displaystyle r_{u}}$ ${\displaystyle d_{k}}$ ${\displaystyle (k+1)\mu }$ ${\displaystyle k}$

${\displaystyle d_{k}=2\,r_{u}\cdot \sin \left({\frac {(k+1)\pi }{n}}\right)=a\cdot \sin \left({\frac {(k+1)\pi }{n}}\right)\cdot \csc \left({\frac {\pi }{n}}\right)}$.

Identity applies to the lengths of the diagonals in a simple regular polygon

${\displaystyle d_{k}=d_{n-k-2}}$.

If the number of corners of the polygon is even, diagonals are therefore of different lengths; if the number of corners is odd, there are diagonals of different lengths. With a given side length , the following explicit formulas for the lengths of the diagonals of simple regular polygons result: ${\displaystyle {\tfrac {n-2}{2}}}$ ${\displaystyle {\tfrac {n-3}{2}}}$ ${\displaystyle a}$

Polygon	Diagonals
	diagonal ${\displaystyle d_{1}}$	diagonal ${\displaystyle d_{2}}$	diagonal ${\displaystyle d_{3}}$	diagonal ${\displaystyle d_{4}}$	diagonal ${\displaystyle d_{5}}$
square	${\displaystyle a\cdot {\sqrt {2}}}$
pentagon	${\displaystyle a\cdot {\tfrac {1}{2}}\left(1+{\sqrt {5}}\right)}$
hexagon	${\displaystyle a\cdot {\sqrt {3}}}$	${\displaystyle a\cdot 2}$
octagon	${\displaystyle a\cdot {\sqrt {2+{\sqrt {2}}}}}$	${\displaystyle a\cdot \left(1+{\sqrt {2}}\right)}$	${\displaystyle a\cdot {\sqrt {2\left(2+{\sqrt {2}}\right)}}}$
decagon	${\displaystyle a\cdot {\sqrt {{\tfrac {1}{2}}\left(5+{\sqrt {5}}\right)}}}$	${\displaystyle a\cdot {\tfrac {1}{2}}\left(3+{\sqrt {5}}\right)}$	${\displaystyle a\cdot {\sqrt {5+2{\sqrt {5}}}}}$	${\displaystyle a\cdot \left(1+{\sqrt {5}}\right)}$
Dodecagon	${\displaystyle a\cdot {\sqrt {2+{\sqrt {3}}}}}$	${\displaystyle a\cdot \left(1+{\sqrt {3}}\right)}$	${\displaystyle a\cdot {\sqrt {3\left(2+{\sqrt {3}}\right)}}}$	${\displaystyle a\cdot \left(2+{\sqrt {3}}\right)}$	${\displaystyle a\cdot 2{\sqrt {2+{\sqrt {3}}}}}$

properties

Symmetries

Axes of symmetry for the regular pentagon and hexagon

The symmetry group of a regular corner is the dihedral group . The dihedral group shows the order and consists of ${\displaystyle n}$ ${\displaystyle D_{n}}$ ${\displaystyle 2n}$

• ${\displaystyle n}$ Rotations of the cyclic group and ${\displaystyle C_{n}}$
• ${\displaystyle n}$ Reflections on the symmetry axes through the center of the polygon.

If it is straight, then one half of the axes of symmetry runs through two opposite corners and the other half through two center points on opposite sides. If odd, then all axes of symmetry run through a corner and the center of the opposite side. ${\displaystyle n}$ ${\displaystyle n}$

Every regular polygon with an even number of corners is also point-symmetric with respect to its center.

Decompositions

Decompositions of a regular heptagon and a regular octagon along all diagonals

The total number of all diagonals in a regular corner results in (sequence A000096 in OEIS ), since diagonals start from each of the corners and with this counting all diagonals are counted twice. In the case of a simple regular polygon with an even number of corners, all diagonals run through the center of the polygon. If the number of corners is odd, the diagonals inside create a reduced copy of the polygon. The number of points of intersection of the diagonals inside a simple regular corner gives the result ${\displaystyle n}$ ${\displaystyle {\tfrac {1}{2}}n(n-3)}$ ${\displaystyle n}$ ${\displaystyle n-3}$ ${\displaystyle n}$

${\displaystyle 0,1,5,13,35,49,\ldots }$   (Follow A006561 in OEIS ).

The result is the number of partial polygons that result from a complete decomposition of a simple regular corner along the diagonal ${\displaystyle n}$

${\displaystyle 1,4,11,24,50,80,\ldots }$   (Follow A007678 in OEIS ).

The number of possibilities to divide a simple regular corner into partial polygons along the diagonal without overlapping is indicated by the small Schröder numbers . If these partial polygons are only to be triangles, the number of possibilities is indicated by the Catalan numbers . In a more general way, decompositions of regular polygons are also examined, in which not only the diagonals may be used, for example the decomposition into triangles of equal area . ${\displaystyle n}$ ${\displaystyle s_{n-2}}$ ${\displaystyle C_{n-2}}$

distances

The sum of the distances from any point inside a regular polygon to the sides is equal to the sum of the distances from the center to the sides

According to Viviani's theorem , the sum of the perpendicular distances from any point inside a simple regular polygon to the sides of the polygon is equal to the sum of the distances from the center to the sides and is therefore equal . If you consider the triangles that are formed by the point and two adjacent corner points, then the sum of the areas of these triangles is equal to the total area of ​​the polygon, that is ${\displaystyle P}$ ${\displaystyle n\cdot r_{i}}$ ${\displaystyle P}$

${\displaystyle {\frac {a}{2}}\,d(P,a)+{\frac {a}{2}}\,d(P,b)+{\frac {a}{2}}\,d(P,c)+\dotsb ={\frac {n\,a\,r_{i}}{2}}}$.

The statement is then obtained by dividing both sides of the equation by . Other identities in regular polygons are: ${\displaystyle {\tfrac {a}{2}}}$

• The sum of the distances from the corner points to any tangent to the circumference is . ${\displaystyle n\cdot r_{u}}$
• The sum of the squares of the distance from the corner points to any point on the perimeter is . ${\displaystyle 2n\cdot (r_{u})^{2}}$
• The sum of the squares of the distances from the centers of the sides to any point on the perimeter is . ${\displaystyle 2n\cdot (r_{u})^{2}-{\tfrac {1}{4}}n\cdot a^{2}}$

The product of the distances from one corner point to all other corner points results in a regular polygon

${\displaystyle \prod _{k=1}^{n-1}2r_{u}\cdot \sin \left({\frac {k\pi }{n}}\right)=n\cdot (r_{u})^{n-1}}$.

Maximality

Of all the hexagons inscribed in a circle, the regular hexagon has the largest area

According to Zenodorus' theorem, regular polygons maximize the area compared to other polygons in the following way:

• Of all corners with the same circumference, the regular corner has the largest area. ${\displaystyle n}$ ${\displaystyle n}$
• Of all the corners inscribed in a given circle , the regular corner has the largest area. ${\displaystyle n}$ ${\displaystyle n}$
• In every finite set of regular polygons with the same circumference, the one with the most corners has the largest area.

On the other hand, the isoperimetric inequality also applies :

• A circle has a larger area than any regular polygon with the same circumference.

construction

Compass and ruler

Construction of a regular seventeenth-corner with compass and ruler after Herbert W. Richmond

→ Main article : Constructible polygon

The question of which regular corners can be constructed using only compasses and rulers was already investigated in antiquity , but it was not finally answered until the 19th century by Carl Friedrich Gauß and Pierre Wantzel . According to this, a regular polygon can be constructed with a compass and ruler if the number of its sides depends on the shape ${\displaystyle n}$

${\displaystyle n=2^{r}p_{1}\cdots p_{k}}$

is, where and in pairs are different Fermat prime numbers . The smallest regular polygon that cannot be constructed is thus the regular heptagon . If one allows an additional aid to divide an angle into three parts , all regular polygons with side numbers are of the form ${\displaystyle r,k\in \mathbb {N} _{0}}$ ${\displaystyle p_{1},\ldots ,p_{k}}$

${\displaystyle n=2^{r}3^{s}p_{1}\cdots p_{k}}$

constructible, where and different Pierpont prime numbers are greater than three. In this way, the regular, for example, heptagon , regular Neuneck and regular Dreizehneck constructible, but not the regular hendecagon . Finding specific construction rules for regular polygons quickly turns out to be very time-consuming as the number of corners increases. However, there are such construction regulations for the 17-corner , the 257-corner and the 65537-corner . ${\displaystyle r,s,k\in \mathbb {N} _{0}}$ ${\displaystyle p_{1},\ldots ,p_{k}}$

Coordinates

The fifth roots of unity in the complex plane

The complex solutions of the circle division equation can be used to calculate the corner points of a regular corner . The polar coordinates of the th corner point of a regular corner with the number of revolutions (for simple polygons is ), the origin of the coordinates as the center, the radius and the angle of rotation thus have the simple form ${\displaystyle n}$ ${\displaystyle z^{n}=1}$ ${\displaystyle (r_{k},\varphi _{k})}$ ${\displaystyle k}$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle m=1}$ ${\displaystyle r_{u}}$ ${\displaystyle \theta }$

${\displaystyle (r_{k},\varphi _{k})=\left(r_{u},{\frac {2\pi km}{n}}+\theta \right)}$.

For , and these vertices correspond to the -th roots of unity in the complex number plane . In a Cartesian coordinate system, the coordinates of the -th corner point are accordingly ${\displaystyle r_{u}=1}$ ${\displaystyle m=1}$ ${\displaystyle \theta =0}$ ${\displaystyle n}$ ${\displaystyle (x_{k},y_{k})}$ ${\displaystyle k}$

${\displaystyle (x_{k},y_{k})=\left(r_{u}\cdot \cos \left({\frac {2\pi km}{n}}+\theta \right),r_{u}\cdot \sin \left({\frac {2\pi km}{n}}+\theta \right)\right)}$.

algorithm

In pseudocode , a regular polygon with corners, the number of revolutions , the circumferential radius and the angle of rotation can be represented as follows: ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle r}$ ${\displaystyle t}$

function regpoly(n,m,r,t)
  for k = 1 to n              // Schleife über die Seiten bzw. Ecken
    w = 2 * pi * m/n;         // Mittelpunktswinkel
    x1 = r * cos(k*w+t);      // Koordinaten (x1,y1) des ersten Eckpunkts
    y1 = r * sin(k*w+t);
    x2 = r * cos((k+1)*w+t);  // Koordinaten (x2,y2) des zweiten Eckpunkts
    y2 = r * sin((k+1)*w+t);
    line(x1,y1,x2,y2)         // Linie von (x1,y1) nach (x2,y2)
  end

Asymptotics

Circle as a border shape

Gradual approach to a circle through inscribed or circumscribed regular polygons

As the number of pages increases , the shape of a simple regular corner with a constant incircle or circumferential radius approaches a circle. The ratio of the circumference and the inscribed or circumferential radius tends towards the limit value ${\displaystyle n}$ ${\displaystyle n}$

${\displaystyle \lim _{n\to \infty }2n\cdot \sin \left({\frac {\pi }{n}}\right)=\lim _{n\to \infty }2n\cdot \tan \left({\frac {\pi }{n}}\right)=2\pi }$.

The ratio of the area and the square of the inscribed circle or the circumferential radius tends towards the limit value for increasing ${\displaystyle n}$

${\displaystyle \lim _{n\to \infty }{\frac {n}{2}}\cdot \sin \left({\frac {2\pi }{n}}\right)=\lim _{n\to \infty }n\cdot \tan \left({\frac {\pi }{n}}\right)=\pi }$.

Page number	Perimeter radius ${\displaystyle r_{u}=1}$				Inscribed radius ${\displaystyle r_{i}=1}$
	Side length	Inscribed radius	scope	Area	Side length	Perimeter radius	scope	Area
${\displaystyle n}$	${\displaystyle 2\cdot \sin \left({\tfrac {\pi }{n}}\right)}$	${\displaystyle \cos \left({\tfrac {\pi }{n}}\right)}$	${\displaystyle 2n\cdot \sin \left({\tfrac {\pi }{n}}\right)}$	${\displaystyle {\tfrac {n}{2}}\cdot \sin \left({\tfrac {2\pi }{n}}\right)}$	${\displaystyle 2\cdot \tan \left({\tfrac {\pi }{n}}\right)}$	${\displaystyle \sec \left({\tfrac {\pi }{n}}\right)}$	${\displaystyle 2n\cdot \tan \left({\tfrac {\pi }{n}}\right)}$	${\displaystyle n\cdot \tan \left({\tfrac {\pi }{n}}\right)}$
3	1.732050808	0.500000000	5.196152423	1.299038106	3,464101615	2.000000000	10.39230485	5.196152423
4th	1.414213562	0.707106781	5.656854249	2.000000000	2.000000000	1.414213562	8.000000000	4.000000000
5	1.17570505	0.809016994	5,877852523	2.377641291	1.453085056	1.236067978	7.265425280	3,632712640
6th	1.000000000	0.866025404	6.000000000	2.598076211	1.154700538	1.154700538	6.928203230	3,464101615
7th	0.867767478	0.900968868	6.074372348	2.736410189	0.963149238	1.109916264	6.742044663	3.371022332
8th	0.765366865	0.923879533	6.122934918	2.828427125	0.828427125	1.082392200	6,627416998	3.313708499
9	0.684040287	0.939692621	6.156362580	2.892544244	0.727940469	1.064177772	6.551464217	3.275732108
10	0.618033989	0.951056516	6.180339888	2,938926261	0.649839392	1.051462224	6,498393925	3.249196962
100	0.062821518	0.999506560	6.282151816	3.139525976	0.062852532	1,000493683	6.285253209	3.142626604
1000	0.006283175	0.999995065	6.283174972	3.141571983	0.006283206	1.000004935	6.283205978	3.141602989
10,000	0.000628319	0.999999951	6.283185204	3.141592447	0.000628319	1.000000049	6.283185514	3.141592757
100,000	0.000062832	0.999999999	6.283185306	3.141592652	0.000062832	1.000000000	6.283185309	3.141592655
${\displaystyle \lim _{n\to \infty }}$	0	1	2 · π	π	0	1	2 · π	π

Apeirogon as a border shape

Regular tiling of the hyperbolic level by Apeirogone

If the length of the sides is kept constant as the number of pages increases, the shape of a simple regular corner approximates a degenerate geometric figure , which is called Apeirogon (from the Greek ἄπειρον , which means unlimited) and is designated by the Schläfli symbol . An Apeirogon can be seen as a string of an infinite number of lines of the same length of the form ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle \{\infty \}}$

... ...

can be visualized or viewed as a circle with an infinitely large radius. The interior angles of an apeirogon are straight angles and therefore measure

${\displaystyle \mu =180^{\circ }=\pi }$.

In hyperbolic space , however, an apeirogon is no longer degenerate and has a number of interesting properties. Thus, the example, can be hyperbolic plane by Apeirogone in various ways regularly parkettieren .

Nesting

Alternating nested circles and regular polygons with increasing number of pages

If a regular triangle is inscribed in a unit circle, then a regular square in its inscribed circle, a regular pentagon in its inscribed circle, and so on, then the sequence of inscribed radii converges towards the limit value

${\displaystyle \prod _{n=3}^{\infty }\cos \left({\frac {\pi }{n}}\right)=0{,}1149420\ldots }$   (Follow A085365 in OEIS ),

the Kepler-Bouwkamp constant or polygon inscribing constant is called. Similarly, if regular polygons with an increasing number of sides and their circumferences are circumscribed alternately around a unit circle, the sequence of the circumferential radii converges towards the limit value

${\displaystyle \prod _{n=3}^{\infty }\sec \left({\frac {\pi }{n}}\right)=8{,}7000366\ldots }$   (Follow A051762 in OEIS ),

known as polygon circumscribing constant .

The product of the two constants is 1.

use

Polygonal numbers

The fourth centered pentagonal number (31) and hexagonal number (37)

In number theory, the polygonal numbers and the centered polygonal numbers are considered, which arise from the fact that regular polygons are laid with a certain number of stones. According to Fermat's theorem of polygons , every prime number can be represented as a sum of at most such corner numbers. A well-known special case of this theorem is the four-squares theorem by Joseph Louis Lagrange . The three-dimensional generalizations of polygonal numbers are called pyramidal numbers . ${\displaystyle n}$ ${\displaystyle n}$

Approximation of π

Principle of the exhaustion method for the step-by-step approximation of the circle number π

Archimedes continued in the 3rd century BC. BC for the first time regular polygons to calculate the number of circles with the help of the exhaustion method . For this he used a sequence of polygons that are inscribed or circumscribed in a unit circle with a radius . He started with the regular hexagon and continued the series with the dodecagon, the 24-corner, the 48-corner up to the 96-corner. That was how he won the estimate ${\displaystyle \pi }$ ${\displaystyle r=1}$

${\displaystyle 3+{\frac {10}{71}}<\pi <3+{\frac {1}{7}}}$.

In the Middle Ages, Chinese and Persian scientists continued these calculations with the 192-corner and other polygons. In the 16th century, Ludolph van Ceulen carried out calculations up to the regular corner and thus determined the number of circles to within 35 digits. In general, the approximation of a circle with inscribed and circumscribed regular corners results in estimates of the shape ${\displaystyle 2^{62}}$ ${\displaystyle \pi }$ ${\displaystyle n}$ ${\displaystyle \pi }$

${\displaystyle {\frac {n}{2}}\cdot \sin \left({\frac {2\pi }{n}}\right)<\pi <n\cdot \tan \left({\frac {\pi }{n}}\right)}$.

The trigonometric terms can be calculated with the help of recursion formulas .

Tiling

Regular polygons as tiles of a tiling used the plane. If only a regular polygon is allowed as a tile, whereby the tiles have to be arranged edge to edge, the three Platonic tiling results from regular triangles, squares and hexagons. If different regular polygons are allowed as tiles, whereby the same arrangement of polygons always have to collide at the corners, one obtains the eight Archimedean tiling . A far greater variety of tiling results if different combinations of polygons are allowed at the corners.

• 

  Hexagonal grid

• 

  3-3-4-3-4

• 

  3-3-3-3-6 (two mirrored versions)

• 

  3-4-6-4

• 

  4-6-12

• 

  3-4-4-6 and 3-6-3-6

polyhedron

In three-dimensional space, regular polygons form the side surfaces of regular polyhedra . If only one regular polygon is used, whereby the same number of polygons always have to collide at the corners, the five Platonic solids tetrahedron , hexahedron , octahedron , dodecahedron and icosahedron are obtained . If different regular polygons are permitted as side surfaces, whereby the same arrangement of polygons must always collide at the corners, the 13 Archimedean solids as well as certain prisms and antiprisms result . If non-uniform corners are also allowed, the 92 Johnson solids are obtained . Some of these polyhedra can also be used to parquet three-dimensional space . There are also star bodies whose faces are regular polygons, such as the star tetrahedron .

• 

  Square pyramid

• 

  Star tetrahedron

• 

  Dodecahedron

• 

  Icosahedron

• 

  Truncated octahedron

• 

  Truncated icosahedron (football body)

• 

  Rhombicosidodecahedron

• 

  Triangular dome

• 

  Pseudo-rhombic cuboctahedron

Occurrence

architecture

The Pentagon from above

Regular polygons are often used in architecture as the floor plan of central buildings. For example are

• square : the Egyptian pyramids , crossing towers in church buildings
• pentagonal : the pentagon in Washington, the fortress Rosenberg in Kronach (see also pentagonal tower , pentagons in architecture and fortress construction )
• hexagonal : Saarlouis fortress , Fort Jefferson in Florida, the telephone kiosks in Denmark (see also occurrence of hexagons and hexagonal structures , list of hexagonal churches )
• Seven-sided : the Liederhalle culture and congress center in Stuttgart, the Princely Mausoleum in Stadthagen
• octagonal : the Dome of the Rock in Jerusalem, the Castel del Monte in Apulia (see also Octagon (architecture) )
• nine-sided : the fortress city of Palmanova , the houses of worship of the Baha'i
• dodecagonal : the Torre del Oro in Seville, the La Vera Cruz church in Segovia (see also dodecagon in architecture )
• fourteen-sided : the Church of Notre-Dame de l'Assomption in Rieux-Minervois
• sixteen-sided : the central building of Aachen Cathedral , the La Malagueta bullring in Málaga

numismatics

Egyptian 2.5 millim coin from 1933

Coins are not always circular, but sometimes have a polygonal shape. Such coins, referred to as cliffs in numismatics , were previously minted as emergency coins , but they are occasionally also found as current or commemorative coins . Examples of floating cliffs in the shape of a regular polygon are:

• square : the 50 cent coin of the Netherlands Antilles
• hexagonal : the Indian 20 paisse coin
• heptagonal : the British 20 and 50 pence coins
• octagonal : the Chilean one and five peso coins
• eleven : the Indian two rupee coin
• twelve-sided : the Australian 50 cent coin

Modern cliffs often have the shape of a Reuleaux polygon with outwardly curved sides so that they can also be recognized by coin machines .

nature

Honeycomb

Regular polygonal structures also occur in nature. Some atoms can form cyclic compounds , such as the benzene ring C ₆ H ₆ in the form of a regular hexagon. Regular polygons also appear in the structure of crystals , for example in cubic or hexagonal crystal systems . In biology, regular polygons can be found in okra fruits (pentagonal) and honeycombs (hexagonal).

symbolism

Some regular polygons have a symbolic meaning in addition to the geometric one , for example the triangle symbol or the pentagram . Road signs , especially right of way signs , often have the shape of a regular polygon with rounded corners.

literature

• Harold Scott MacDonald Coxeter : Regular Polytopes . Courier Dover Publications, 1973, ISBN 0-486-61480-8 .
• John M. Lee: Axiomatic Geometry . American Mathematical Society, 2013, ISBN 978-0-8218-8478-2 .
• Roger A. Johnson: Advanced Euclidean Geometry . Dover Publications, 2007, ISBN 978-0-486-46237-0 .

Web links

Commons : Regular polygons  - collection of images, videos, and audio files

• Regular polygons . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
• Eric W. Weisstein : Regular Polygon . In: MathWorld (English).
• Wkbj79: Regular polygon . In: PlanetMath . (English)
• Jürgen Köller: Regular polygon. In: Mathematical handicrafts. 2005, accessed November 7, 2014 . 
• Edmund Weitz : The regular 17-sided. In: YouTube. 2017, accessed August 27, 2020 . 

Individual evidence

1. ^ ^{A b c} Harold Scott MacDonald Coxeter: Regular Polytopes . Courier Dover Publications, 1973, pp. 2 .
2. ^ Siegfried Völkel, Horst Bach, Heinz Nickel, Jürgen Schäfer: Mathematics for technicians . Carl Hanser Verlag, 2014, p. 169 .
3. ↑ ^{a b c d} Hans-Jochen Bartsch: Pocket book of mathematical formulas for engineers and natural scientists . Carl Hanser Verlag, 2014, p. 141-143 .
4. ↑ Bjorn Poonen , Michael Rubinstein: The number of intersection points made by the diagonals of a regular polygon . In: SIAM J. Discrete Mathematics . tape 11 , no. 1 , 1998, p. 135-156 .
5. ^ Roger A. Johnson: Advanced Euclidean Geometry . Dover Publications, 2007, pp. 72 .
6. ^ Herbert W. Richmond: A Construction for a regular polygon of seventeen sides . In: The Quarterly Journal of Pure and Applied Mathematics . tape 26 , 1893, pp. 206-207 ( description and illustration (Fig. 6) ).
7. ↑ Andrew Gleason : Angle Trisection, the Heptagon, and the Triskaidecagon . In: The American Mathematical Monthly . tape 95 , no. 3 , 1988, pp. 185–194 ( FIG.1. Construction of a regular heptagon, page 186 ff., PDF accessed on May 15, 2019).
8. ↑ Andrew Gleason : Angle Trisection, the Heptagon, and the Triskaidecagon . In: The American Mathematical Monthly . tape 95 , no. 3 , 1988, pp. 185–194 ( FIG. 4. Construction of a regular triskaidecagon., Page 193 ff., PDF accessed on May 15, 2019).
9. ^ ^{A b} Harold Scott MacDonald Coxeter: Regular Polytopes . Courier Dover Publications, 1973, pp. 3 .
10. ↑ Harold Scott MacDonald Coxeter: Regular Polytopes . Courier Dover Publications, 1973, pp. 45 .