Pyramid (geometry)

The pyramid is a geometric body , more precisely a polyhedron , whose base is a polygon and whose side surfaces are triangles , which on the one hand are adjacent to the polygon and on the other hand meet at a point, the so-called tip of the pyramid. The polygon is also called the base of the pyramid. The triangles together form the outer surface of the pyramid.

construction

From an excellent point , the pyramid top, a pencil of rays is based, whose radiation is a plane cut in the corners of the base of the pyramid. With four rays of a certain inclination in the room you get a square base, for example, and thus form the square pyramid. You can also start the construction with any base area of ​​a polygon of the plane and choose a point outside this plane, which then becomes the pyramid tip. By connecting every corner of the base with the tip, the aforementioned bundle of rays is created. The points of each individual base edge are connected to the pyramid tip via the triangular surface. The pyramid thus also fulfills the definition of a cone .

properties

If the base of a pyramid has corners , the number of triangular side surfaces is also the same. Together with the base, the pyramid then has a total of surfaces . The number of corners is also namely corners in the base plus the tip. The base contains edges. Together with the just as many side lines of the bundle of rays that connect the corners of the base with the pyramid tip, the pyramid as a whole has edges. In the case of the pyramid, this count confirms Euler's polyhedron substitution via the number of corners, the number of edges and the number of faces of a polyhedron: ${\displaystyle n}$ ${\displaystyle n.}$ ${\displaystyle n+1}$ ${\displaystyle n+1,}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle 2\cdot n}$ ${\displaystyle E}$ ${\displaystyle K}$ ${\displaystyle F}$

${\displaystyle E-K+F=(n+1)-2\cdot n+(n+1)=2}$

For the calculation of the volume , the concept of the height of a pyramid is important. This means the distance between the pyramid tip and the plane in which the base is located.

The center of gravity of a pyramid lies on the connection between the center of gravity of the base and the top of the pyramid. It divides this distance in the ratio 1: 3 and therefore has the distance from the base plane. ${\displaystyle {\tfrac {h}{4}}}$

Regular pyramid

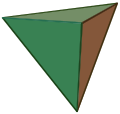
A pyramid whose base is an equilateral triangle and whose three side surfaces are triangles that are congruent to the base is called a regular tetrahedron .

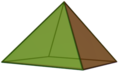
A pyramid whose base is a square and whose pyramid tip is perpendicular to the center of the base is called a square pyramid.

Tetrahedron and square pyramids are so-called regular or regular pyramids. One speaks of a regular or regular pyramid when the base of the pyramid is a regular polygon and the center of this polygon is also the base of the pyramid height. The other side faces are therefore isosceles triangles . Every regular pyramid is therefore also straight (see section Straight pyramid ).

A regular pyramid is completely determined by three defining pieces, for example if the number of corners / edges of the base, the side length of the base and the height are given.

• 

  Tetrahedron

• 

  Square pyramid

• 

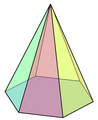
  Regular five-sided pyramid

• 

  Regular six sided pyramid

Formulas

Sizes of a regular pyramid (regular n- corner with side length a as base and height a )
	General case	Square pyramid	Regular triangular pyramid
volume	${\displaystyle V={\frac {n\cdot a^{2}\cdot h}{12}}\cdot \cot \left({\frac {\pi }{n}}\right)}$	${\displaystyle V={\frac {a^{2}\cdot h}{3}}}$	${\displaystyle V={\frac {a^{2}\cdot h}{12}}\cdot {\sqrt {3}}}$
Surface area	${\displaystyle O={\frac {n\cdot a}{4}}\cdot \left(a\cdot \cot \left({\frac {\pi }{n}}\right)+{\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)}$	${\displaystyle O=a^{2}+a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}}$	${\displaystyle O={\frac {3\cdot a}{4}}\cdot \left({\frac {a}{3}}\cdot {\sqrt {3}}+{\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}\right)}$
Steep edge length	${\displaystyle l=\left(h^{2}+{\frac {a^{2}}{4\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}}$	${\displaystyle l={\sqrt {h^{2}+{\frac {a^{2}}{2}}}}}$	${\displaystyle l={\sqrt {h^{2}+{\frac {a^{2}}{3}}}}}$
Umkugelradius	${\displaystyle r_{u}={\frac {h}{2}}+{\frac {a^{2}}{8\cdot h\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)}}}$	${\displaystyle r_{u}={\frac {h}{2}}+{\frac {a^{2}}{4\cdot h}}}$	${\displaystyle r_{u}={\frac {h}{2}}+{\frac {a^{2}}{6\cdot h}}}$
Inc sphere radius	${\displaystyle r_{i}={\frac {a\cdot h}{a+{\sqrt {4\cdot h^{2}\cdot \tan ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}}}}}$	${\displaystyle r_{i}={\frac {a\cdot h}{a+{\sqrt {4\cdot h^{2}+a^{2}}}}}}$	${\displaystyle r_{i}={\frac {a\cdot h}{a+{\sqrt {12\cdot h^{2}+a^{2}}}}}}$
Inner angle of the regular base	${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }}$	${\displaystyle \alpha =90^{\circ }}$	${\displaystyle \alpha =60^{\circ }}$
Base angle of the isosceles triangles	${\displaystyle \alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)}$	${\displaystyle \alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+a^{2}}}\right)}$	${\displaystyle \alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}\cdot {\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}\right)}$
Angle at the apex of the isosceles triangles	${\displaystyle \alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}}\right)}$	${\displaystyle \alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+a^{2}}}}\right)}$	${\displaystyle \alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}}\right)}$
Angle between base and isosceles triangles	${\displaystyle \beta _{1}=\arctan \left({\frac {2\cdot h\cdot \tan \left({\frac {\pi }{n}}\right)}{a}}\right)}$	${\displaystyle \beta _{1}=\arctan \left({\frac {2\cdot h}{a}}\right)}$	${\displaystyle \beta _{1}=\arctan \left({\frac {2\cdot {\sqrt {3}}\cdot h}{a}}\right)}$
Angle between the isosceles triangles	${\displaystyle \beta _{2}=2\cdot \arctan \left({\frac {1}{2\cdot h}}\cdot \left({\frac {4\cdot h^{2}\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}{\tan ^{2}\left({\frac {\pi }{n}}\right)-\sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}\right)}$	${\displaystyle \beta _{2}=2\cdot \arctan \left({\frac {1}{2\cdot h}}\cdot {\sqrt {4\cdot h^{2}+2\cdot a^{2}}}\right)}$	${\displaystyle \beta _{2}=2\cdot \arctan \left({\frac {1}{3\cdot h}}\cdot {\sqrt {3\cdot h^{2}+a^{2}}}\right)}$
Solid angle on the base	${\displaystyle \Omega _{1}=4\cdot \arctan \left({\sqrt {\tan \left({\frac {2\cdot \beta _{1}+\beta _{2}}{4}}\right)\cdot \tan \left({\frac {2\cdot \beta _{1}-\beta _{2}}{4}}\right)\cdot \tan ^{2}\left({\frac {\beta _{2}}{4}}\right)}}\right)}$
Solid angle at the top	${\displaystyle \Omega _{2}=2\cdot \pi -2\cdot n\cdot \arcsin \left(\cos \left({\frac {\pi }{n}}\right)\cdot {\sqrt {\tan ^{2}\left({\frac {\pi }{n}}\right)-\tan ^{2}\left({\frac {\alpha _{3}}{2}}\right)}}\right)}$

Special cases

For certain values ​​of and there are connections with platonic solids : ${\displaystyle n}$ ${\displaystyle h}$

• For and we get the regular tetrahedron . ${\displaystyle n=3}$ ${\displaystyle h={\frac {a}{3}}\cdot {\sqrt {6}}}$
• For and the result is a square pyramid that is one half of the octahedron . ${\displaystyle n=4}$ ${\displaystyle h={\frac {a}{2}}\cdot {\sqrt {2}}}$
• For and there is a regular five-sided pyramid that is part of the icosahedron . ${\displaystyle n=5}$ ${\displaystyle h={\frac {a}{10}}\cdot {\sqrt {50-10\cdot {\sqrt {5}}}}}$

Straight pyramid

Straight pyramid

If the tip of a pyramid is positioned above its base in such a way that the silhouette appears as an isosceles triangle to an observer who is in the plane of the base from as many directions as possible , then it is called straight .

If the base is rotationally symmetrical , then in the case of straight pyramids the plumb point coincides with the center of symmetry or the center of gravity of the base. If the base area is not only rotationally symmetrical, but also a regular polygon , then all side edges, ie all edges that start from the tip, are of the same length.

In the case of a straight pyramid with a dragon square as the base, the base point is in the middle of the diagonals , which is the axis of symmetry and not at the intersection of the diagonals or the center of gravity .

The base of a pyramid has no symmetries on, then the term has just not a sensible meaning more: If the base area for example, any triangle , so must the top of the pyramid vertically above its circumcenter lie, so that all side edges are of equal length. If this triangle is further obtuse angled , then the plumb point of the tip even lies outside the base area - which contradicts the illustrative meaning of straight .

Leaning pyramid

Leaning pyramid

A pyramid with a regular polygon as a base is called skewed if not all side edges are of the same length, the base of the perpendicular from the tip is not in the center of the base and therefore the connecting line from and not perpendicular to the base of the pyramid. In the case of a crooked pyramid, the base point of the perpendicular from the tip can therefore be both inside and outside the pyramid base. ${\displaystyle S}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle S}$ ${\displaystyle S}$

Johnson bodies J ₁ and J ₂

A square pyramid, the four triangular faces of which are equilateral, is the simplest Johnson field , abbreviated as J ₁ . The regular five-sided pyramid, the five triangular sides of which are equilateral, is the Johnson field J ₂ .

Square pyramid

Lateral surface and surface

Surface of a square pyramid as a network of bodies

The surface of a square pyramid consists of the square base and the outer surface ${\displaystyle G}$ ${\displaystyle M.}$

If the side length of the square is given, we get : ${\displaystyle a}$ ${\displaystyle G=a^{2}}$

${\displaystyle O=a^{2}+M}$

In the case of a regular pyramid with a square base, the outer surface is made up of four surfaces of congruent isosceles triangles .

Let the side length and the pyramid height be given: ${\displaystyle a}$ ${\displaystyle h}$

The area of ​​one of these triangles is , that is , of all four areas . Here is the height of the congruent side triangles. ${\displaystyle A_{D}={\frac {a\cdot h_{a}}{2}}}$ ${\displaystyle M=2\cdot a\cdot h_{a}}$ ${\displaystyle h_{a}}$

From the Pythagorean theorem follows . It follows from this and therefore for the lateral surface ${\displaystyle {h_{a}}^{2}=h^{2}+({\tfrac {a}{2}})^{2}}$ ${\displaystyle h_{a}={\sqrt {h^{2}+({\tfrac {a}{2}})^{2}}}}$ ${\displaystyle M=a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}.}$

The total surface is thus . ${\displaystyle O=a^{2}+a\cdot {\sqrt {4\ h^{2}+a^{2}}}}$

Steep edge length

In addition to the four edges of the base , the square pyramid also has four steep edges of equal length (also called ridges) , which start from the corner points of the base and rise upwards and meet at the top of the pyramid . ${\displaystyle a}$ ${\displaystyle AS,BS,CS}$ ${\displaystyle DS,}$ ${\displaystyle S}$

Let the side length and the pyramid height be given: ${\displaystyle a}$ ${\displaystyle h}$

The Pythagorean theorem gives the length of the base diagonal from which it follows. ${\displaystyle d}$ ${\displaystyle d^{2}=a^{2}+a^{2},}$ ${\displaystyle d=a\cdot {\sqrt {2}}}$

For the further calculation one needs and the square of it is ${\displaystyle {\tfrac {d}{2}}={\tfrac {a}{2}}\cdot {\sqrt {2}}}$ ${\displaystyle {\tfrac {a^{2}}{2}}.}$

The Pythagorean theorem is used again to calculate from : and this then follows for the ridge . ${\displaystyle AS}$ ${\displaystyle {AS}^{2}=h^{2}+{\tfrac {a^{2}}{2}}}$ ${\displaystyle AS={\sqrt {h^{2}+{\tfrac {a^{2}}{2}}}}}$

Total edge length

The total edge length of the square pyramid is made up of the four side lengths and the four equally long ridges and . Again, let the side length and the pyramid height be given: ${\displaystyle K}$ ${\displaystyle a}$ ${\displaystyle AS,BS,CS}$ ${\displaystyle DS}$ ${\displaystyle a}$ ${\displaystyle h}$

${\displaystyle K=4\cdot a+4\cdot {\sqrt {h^{2}+{\frac {a^{2}}{2}}}}}$

${\displaystyle K=4\cdot \left(a+{\sqrt {h^{2}+{\frac {a^{2}}{2}}}}\right)}$

Volume as an extreme value

Paper model of a square pyramid with maximum volume for a given surface

The sphere is a body whose volume is maximal for a given surface, i.e. H. any change in the external shape would result in a smaller volume. Similarly, the cube, the regular tetrahedron and the regular octahedron have the largest volume among all polyhedra with the same surface and the same number of corners.

A square pyramid with maximum volume, on the other hand, is comparatively pointed: of all square pyramids with the same surface, the one that is tall has the largest volume (if the length of its base indicates the largest volume ). Its volume is , the triangles of its lateral surface are high. ${\displaystyle h=a\cdot {\sqrt {2}}}$ ${\displaystyle a}$ ${\displaystyle V={\frac {1}{3}}\cdot a^{3}\cdot {\sqrt {2}}}$ ${\displaystyle {\frac {3}{2}}\cdot a}$

General pyramid

volume

The volume of a pyramid is calculated from the content of the base and the height according to ${\displaystyle V}$ ${\displaystyle G}$ ${\displaystyle h}$

${\displaystyle V={\frac {1}{3}}\cdot G\cdot h.}$

This formula applies to any pyramid. So it doesn't matter whether the base is a triangle, square, pentagon, ... The formula is also valid if the height base point does not coincide with the center point of the base area or the base area has no center point at all. In the special case of a square pyramid, the result is where the side length of the square base area is and the height is. ${\displaystyle V={\frac {1}{3}}\cdot a^{2}\cdot h}$ ${\displaystyle a}$ ${\displaystyle h}$

Incidentally, the general formula corresponds to the volume formula for a circular cone . This is because each pyramid meets the definition of a general cone. Conversely, a cone can also be understood as a pyramid with a regular -gon as the base area, which has degenerated into a circle after the border crossing . ${\displaystyle V={\frac {1}{3}}\cdot G\cdot h}$ ${\displaystyle V={\frac {1}{3}}\cdot \pi \cdot r^{2}\cdot h}$ ${\displaystyle n}$ ${\displaystyle n\to \infty }$

Calculation using the late product

One of the vectors , , spanned three-sided pyramid, the volume ${\displaystyle {\vec {a}}}$ ${\displaystyle {\vec {b}}}$ ${\displaystyle {\vec {c}}}$

${\displaystyle V={\frac {1}{6}}\cdot |({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}|}$.

Elementary geometric justification

The volume formula mentioned can be justified in two basic steps:

• 1. A cube can be divided into three equal pyramids with a square base, the tips of which coincide in one corner of the cube. The three base surfaces are the three side surfaces of the cube that do not contain this common point.

• 2. Two pyramids with the same base area and height have the same volume.

To prove this statement, one can use Cavalieri's principle and the laws of centric elongation .

The volume formula therefore applies to pyramids . ${\displaystyle V={\frac {1}{3}}\cdot G\cdot h}$

Justification with the help of integral calculus

The volume of a pyramid with the base area and height can be calculated if the pyramid is imagined to be composed of thin ( infinitesimal ) layers of thickness parallel to the base area. Now place an axis through the top of the pyramid so that the height coincides with the axis. If one denotes the area of ​​the layer at a distance from the tip with , one can derive a formula from the laws of centric stretching : ${\displaystyle G}$ ${\displaystyle h}$ ${\displaystyle \mathrm {d} y}$ ${\displaystyle y}$ ${\displaystyle h}$ ${\displaystyle y}$ ${\displaystyle y}$ ${\displaystyle A(y)}$ ${\displaystyle A(y)}$

${\displaystyle A(y):G=y^{2}:h^{2}}$

${\displaystyle A(y)={\frac {G}{h^{2}}}y^{2}}$

This results in the volume of the pyramid by integration of up to the Cavalieri's principle : ${\displaystyle y=0}$ ${\displaystyle y=h}$

${\displaystyle V=\int _{0}^{h}A(y)\,\mathrm {d} y=\int _{0}^{h}{\frac {G}{h^{2}}}y^{2}\,\mathrm {d} y={\frac {G}{h^{2}}}\int _{0}^{h}y^{2}\,\mathrm {d} y={\frac {G}{h^{2}}}\cdot {\frac {1}{3}}\left[y^{3}\right]_{0}^{h}={\frac {G}{h^{2}}}\cdot {\frac {1}{3}}\left[h^{3}-0\right]={\frac {1}{3}}G\cdot h}$

Measurement of a pyramid structure

Viewing from a distance and determining the viewing angle in a simplified form

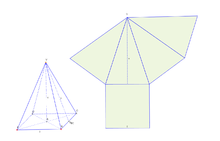
With a large pyramid, the edge lengths of the base can be measured directly, but not the height, which is not directly accessible. In the following, the fundamental difficulties will be presented, which are not so much related to the methodology of the measurement process itself. A simple geometric method for determining the height of larger objects is the observation from a distance and the determination of the viewing angle (shown in a simplified form by the adjacent graphic).

At a distance from the lower edge of the pyramid, the point of the pyramid is sighted at the measured angle . The distance between the observation point and the top of the pyramid in the horizontal line is half of the base . The height results from the formula in the graphic. So determining the height would not be a big problem. However, there are the following difficulties: ${\displaystyle s}$ ${\displaystyle \alpha }$ ${\displaystyle a/2+s}$ ${\displaystyle h}$

• The top of the pyramid is not necessarily exactly above the center of the base.
• The length of the base edge of the pyramid cannot be precisely determined (broken stones, erosion).
• The tip is no longer there (worn off).
• The angle of inclination of the pyramid is difficult to determine (erosion, erosion).

This largely corresponds to the reality of the well-known great pyramids. The height deviation of the observation point at which the measurement is made must be taken into account precisely. The angle measurement itself can usually be carried out very precisely. In addition, it must be defined from which ground level the height of the pyramid should be valid, i.e. where it should actually begin. Assume that the base length of the pyramid cannot be determined more precisely than 30 cm and thus the distance to the measuring point cannot be determined more precisely than 15 cm. As a result, with an assumed viewing angle of 35 °, the height would be inaccurate by the amount of about 10 cm. What is missing now is the determination of the angle of inclination over the side surface. A hypothetical large pyramid with a base length of 200 m and a height of 140 m would have an inaccuracy of the inclination angle of about one arc minute with an inaccuracy of the height specification of 10 cm (54 ° 27'44 " compared to 54 ° 26'34" with ). This now applies to pyramids whose top is still there. The reality is different. The height determination does not reflect the original height, but the height of the removed pyramid. ${\displaystyle \alpha }$ ${\displaystyle a}$ ${\displaystyle a/2+s}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle h=140{,}0\,\mathrm {m} }$ ${\displaystyle h=139{,}9\,\mathrm {m} }$

Problem with extrapolation

So the peak has to be extrapolated . The adjacent picture shows the problem schematically. Both the side surfaces and the tip are clearly worn away by demolition and weathering:

The height would therefore be accessible according to the formula from the direct determination of the angle of inclination . As can be seen, the determination is fraught with great errors. The Chephren pyramid is an exception because it still has the original capstones in the upper part. The angle can thus be determined more precisely than with the other pyramids. This explains the good agreement between the various authors regarding the angle of inclination. ${\displaystyle h}$ ${\displaystyle \beta }$ ${\displaystyle \beta }$

This makes it clear that with real pyramids, neither the height to the centimeter nor the angle of inclination to the arc second can be specified exactly.

Related terms

Related shapes in geometry are the truncated pyramid (a pyramid "cut off" parallel to the base) and the double pyramid (a polyhedron made from two mirror-symmetrical pyramids with the same base).

A hyper pyramid is a generalization to dimensions. The pyramid described in this article is a three-dimensional hyper pyramid. A two-dimensional hyperpyramid would be a triangle, a four-dimensional one a pentachoron . ${\displaystyle n}$

The article Pyramid (building) deals with the pyramid in architecture .

Web links

Commons : Pyramids (geometry)  - collection of images, videos and audio files

• Eric W. Weisstein : Pyramid . In: MathWorld (English).