Dragon square

convex dragon square

concave dragon square

A dragon square (also dragon or deltoid ) is a flat square ,

• where a diagonal is the axis of symmetry ,

or

• that has two pairs of adjacent sides of equal length.

Both definitions are equivalent.

Often, only which is convex form of the deltoids called kite quadrilateral and the concave shape as arrow square or wind bird quadrilateral . The name dragon square refers to the shape of many kites .

A special dragon square is the rhombus . It is an equilateral deltoid .

properties

The following applies to every dragon square (see illustration):

• The diagonals are perpendicular to each other, ie the dragon square is an orthodiagonal square .
• The diagonal , which is the axis of symmetry , bisects the other diagonal and the interior angles in the corner points and . It divides the square into two congruent mirror-symmetrical triangles . ${\displaystyle AC}$ ${\displaystyle BD}$ ${\displaystyle A}$ ${\displaystyle C}$ ${\displaystyle ABCD}$
• The diagonal divides the dragon square into two isosceles triangles . ${\displaystyle BD}$
• The opposite angles in the corner points and are the same size. ${\displaystyle B}$ ${\displaystyle D}$

For every convex dragon square the following applies:

• It has an inscribed circle and is therefore a tangent square .
• It is a chordal quadrilateral if the two equal angles are in the corner points and right angles . This results from the reversal of Thales' theorem . It then has a perimeter . ${\displaystyle B}$ ${\displaystyle D}$

A tangent square is a dragon square if and only if one of the following conditions is met:

• Two adjacent sides are the same length.
• The diagonals are orthogonal .
• The connecting lines of the tangent points are of the same length.
• Two opposite tangent sections are of equal length.
• The center of the circle is on a diagonal .

Formulas

Mathematical formulas for the dragon square
Area	${\displaystyle A=a\cdot b\cdot \sin(\beta )}$
	${\displaystyle A={\frac {e\cdot f}{2}}}$
scope	${\displaystyle U=2\cdot a+2\cdot b=2\cdot (a+b)}$
Side lengths	${\displaystyle a=d,\quad b=c}$
Length of the diagonal (see cosine law , Heron's theorem )	${\displaystyle e={\sqrt {a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos(\beta )}}}$
	${\displaystyle f={\frac {4\cdot {\sqrt {s\cdot (s-a)\cdot (s-b)\cdot (s-e)}}}{e}}}$ With ${\displaystyle s={\frac {a+b+e}{2}}}$
	${\displaystyle f=2\cdot a\cdot \sin \left({\frac {\alpha }{2}}\right)=2\cdot b\cdot \sin \left({\frac {\gamma }{2}}\right)}$
Inscribed radius	${\displaystyle r={\frac {2\cdot A}{U}}={\frac {e\cdot f}{2\cdot (a+b)}}}$
Interior angle (see cosine law )	${\displaystyle \alpha =\arccos \left({\frac {2\cdot a^{2}-f^{2}}{2\cdot a^{2}}}\right)}$
	${\displaystyle \gamma =\arccos \left({\frac {2\cdot b^{2}-f^{2}}{2\cdot b^{2}}}\right)}$
	${\displaystyle \beta =\delta =\arccos \left({\frac {a^{2}+b^{2}-e^{2}}{2\cdot a\cdot b}}\right)}$

Generalizations

An inclined dragon square is a flat square in which one of the diagonals is halved by the other. Such a square is sometimes called crooked . In the case of an inclined dragon square, the diagonals are not necessarily orthogonal to one another. In this sense, the kite square is a straight kite . For the inclined dragon square, a generalized formula for the area applies via the cross product .

A square is a crooked kite if it can be broken down into four equal triangles from an inner point with straight connections to the four corners .

Parquet with dragon squares

Some special tiling contain dragon squares. The Penrose parquet flooring is particularly well known .

• 

  A Penrose tiling

• 

  Dragon squares each with two right angles and one 60 ° angle cut from the axis of symmetry

Polyhedron with dragon squares

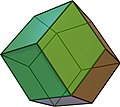
Some polyhedra have kite quadrilaterals as faces . The surface of the deltoidal icositetrahedron and deltoidal hexacontahedron , two Catalan solids , consists of congruent dragon squares.

The rhombohedron , the rhombic dodecahedron, and the rhombic triacontahedron even have diamonds as side faces . The polyhedra mentioned are rotationally symmetrical , ie they can be mapped onto themselves by rotating about certain axes of rotation .

• 

  Rhombohedron

• 

  Rhombic dodecahedron

• 

  Rhombic triacontahedron

• 

  Deltoidal icositetrahedron

• 

  Deltoid hexacontahedron

Individual evidence

1. ↑ Curriculum - preparatory courses for work teachers
2. ↑ Martin Josefsson: When is a Tangential Quadrilateral a Kite? , Forum Geometricorum
3. ^ Dragon Quadrilaterals , Mathematics, TU Freiberg
4. ↑ Jürgen Köller: Hierarchy of the squares , mathematical handicrafts
5. ↑ Hans Walser: Viereck-Viertelung

Web links

Commons : Drachenviereck  - Collection of pictures, videos and audio files

Wiktionary: Drachenviereck  - explanations of meanings, word origins, synonyms, translations