The cosine law is one of the fundamental theorems of geometry and here belongs to the field of trigonometry . It is closely related to the Pythagorean theorem .
The law of cosines is very easy to formulate for plane triangles ; for spherical ones it requires six trigonometric functions . In both cases, it contains three identity equations that represent the relationships between the lengths of the sides of triangles and the cosines of their angles .
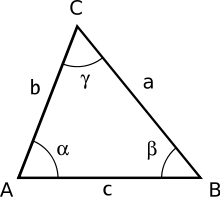
Theorem of cosines for plane triangles
General formulation
For the three sides , and of a triangle, as well as the angle opposite the side (i.e. the angle between the sides and ) :








Inversion for the angle:

The same applies to the other angles:


Equivalent formulation
The three identity equations mentioned above are in turn consequences of the following three cosine formulas and, in the context of trigonometry of the Euclidean plane, are even equivalent to



These formulas are summarized under the keyword projection sentence or projection sentences.
The Pythagorean theorem as a special case of the cosine law
With , i.e. for a right triangle , applies . This results in the Pythagorean theorem as a special case of the cosine law in a right triangle :



The cosine law therefore represents a generalization of the Pythagorean theorem and is also called the Pythagorean extended theorem .
Cosine law for spherical triangles
When spherical cosine law for spherical triangles the length of the sides of the triangle is in the angular indicate why instead of a trigonometric function whose six occur. The analogue to the plane sentence

is therefore
-
 ,
,
Note that the sign is reversed. This side cosine law (here for c, analogously for sides a and b) is opposed to the angle cosine law :
-
 ,
,
where the first sign is negative.
Applications
Numerical example
The following page sizes are known in a triangle ABC (designations as usual):



We are looking for the angle size (designations as usual).





Congruence clauses
The congruence theorems SSS and SWS state that a triangle is completely determined by specifying three sides or two sides and their intermediate angle. Alternatively, you can also specify two vectors from which the included angle can be calculated. In these cases, the law of cosines allows a fourth piece to be calculated from the three given pieces, namely an angle (in the case of SSS) or the third side (in the case of SWS). If you then want to determine the other angles of a triangle, you can either use the law of cosines again (with side names adapted to the angle you are looking for) or the law of sines . The last angle is best calculated using the sum of the angles of 180 °.
If only one side and two angles are given ( congruence theorem SWW or WSW) or two sides and the opposite angle of the larger side ( congruence theorem SsW), one first calculates one of the missing pieces with the sine law and the missing angle using the angle sum, before one can determine the third side with the cosine law.
generalization
With vectors in real scalar product spaces , that is, vector spaces with scalar product , the cosine law can also be easily generalized. Designated



the scalar product norm , i.e. the length, of a vector and with



the angle between the two vectors , then the following applies to the norm of the vector :



proof
Elementary geometric proof
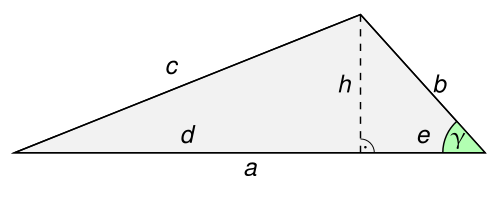
The following proof is assumed. For the proof needs to be modified slightly. For , the cosine law results directly from the Pythagorean theorem .



In the partial triangles, the Pythagorean theorem should be used to find an arithmetic expression for . For this you need the squares of the cathetus lengths of this partial triangle:

-
 ( Pythagorean theorem for the right partial triangle)
( Pythagorean theorem for the right partial triangle)
-
 ( binomial formula )
( binomial formula )
According to Pythagoras, the following applies to the left partial triangle:

So the two arithmetic expressions found above must be added:

Additionally applies

with the inference
-
 .
.
Inserting this intermediate result into the equation for yields the claim:


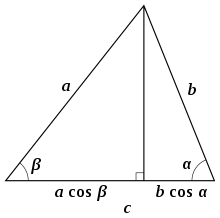
Trigonometric proof
If you draw the plumb line on the side , it is divided into two sections and the following applies:


Multiplication with gives


The equations for the other two sides are obtained analogously


If one adds these two equations, then it follows


Because the right side of the last equation and the right side of coincide, the two left sides can be equated:


Proof by means of vector calculation
Following the presentation by Gericke and Raith, the proof of the three cosine formulas is first carried out:
For this one makes the determinations
-
 .
.
This yields the equations

as well as using the properties of the scalar product

and
-
 .
.
Now draw the basic equation characteristic of the triangle

come up and win

and further
-
 .
.
Hence it results

and thus the first of the above three cosine formulas.
The other two are obtained in the same way.
The three formulas of the general formulation can then be inferred by means of elementary algebraic operations . The first equation is obtained by multiplying the three cosine formulas above with , and , adding up and solving for .




See also
Sources and literature
-
Ilka Agricola , Thomas Friedrich : Elementary Geometry . Expertise for studies and mathematics lessons (= studies ). 4th, revised edition. Springer Spectrum , Wiesbaden 2015, ISBN 978-3-658-06730-4 , doi : 10.1007 / 978-3-658-06731-1 .
-
Heinrich Behnke , Friedrich Bachmann , Kuno Fladt , Wilhelm Süss (eds.): Fundamentals of mathematics . Volume II. Geometry. Vandenhoeck & Ruprecht , Göttingen 1960.
-
IN Bronstein , KA Semendjajev , G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik . 7th, completely revised and expanded edition. Verlag Harri Deutsch , Frankfurt am Main 2008, ISBN 978-3-8171-2007-9 .
-
Hanfried Lenz : Fundamentals of elementary mathematics . 3rd, revised edition. Hanser Verlag , Munich (among others) 1976, ISBN 3-446-12160-9 .
- Manfred Leppig (Ed.): Learning levels in mathematics . 1st edition. Girardet, Essen 1981, ISBN 3-7736-2005-5 , pp. 192-193 .
Web links
References and footnotes
-
^ Proof see also: Wikibooks evidence archive
-
↑ a b c Helmuth Gericke , F. Raith : Vectors and Trigonometry. in: H. Behnke et al .: Fundamentals of Mathematics. Volume II. Geometry. , 1960, p. 266 ff
-
↑ Hanfried Lenz: Fundamentals of elementary mathematics. , 1976, p. 236
-
^ IN Bronstein, KA Semendjajev et al .: Taschenbuch der Mathematik. 2008, p. 146
-
↑ As a consequence of the projection theorem, there is another interesting cosine formula; see evidence archive .
-
↑ The proof of the projection theorem can also be carried out within the framework of elementary geometry, in a similar way to the previous proof.
-
↑ It should be assumed that there is a non-degenerate triangle, i.e. none of the three sides and therefore none of the three vectors has the length .