multiplication
The multiplication ( Latin multiplicatio from multiplicare , multiply ', even Multiplication called) is one of the four basic arithmetic operations in the arithmetic . Its reverse operation is division . The arithmetic operators for multiplication is the mark "·" or "x".
Naming
The multiplication of natural numbers is created by repeatedly adding ( adding up ) the same summand :
and are called factors , which are also referred to as a multiplier and a multiplicand .
The calculation, pronounced “ times ”, is called multiplication. The result product .
For example, one writes for and speaks this term as "three times four". Or is sometimes written instead of .
When multiplying by variables , the point is often left out . For correct spelling see Malzeichen .
When multiplying several or many numbers you can use the product symbol (derived from the large Greek pi ):
are whole numbers, is called a run variable . In the case one has the empty product , which is defined as .
Examples:
or
The faculty often used in combinatorics is a special multiplication of natural numbers:
Repeated multiplying by the same factor leads to exponentiation , e.g. B. is
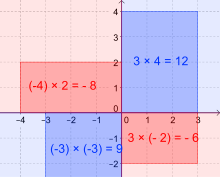
The clear generalization of the multiplication and its calculation rules to the rational and real numbers is achieved by looking at a rectangle with the side lengths and (in a given unit of length). The area of this rectangle (in the corresponding unit of area) is defined as the product .
The multiplication of rational numbers can also be formally defined with the help of fractions. Likewise one can define the multiplication during the construction process of the real from the rational numbers.
The reverse operation for multiplication is division , which can also be interpreted as multiplication with the reciprocal value .
Laws of Calculation
In a body (i.e. in particular , or ) apply to all (see mathematics )
| Associative law | |
| Commutative law | |
| Distributive law | |
| neutral element | |
| inverse element | |
| absorbent element |
Commutativity
In view of the different roles of multiplier (multiplier) on the one hand and multiplicand (multiplier) on the other hand, it is not entirely self-evident that multiplication is commutative, i.e. H. the same thing comes out when changing roles. Through complete induction and with the help of the left and the right distributive law (which themselves can again be proven by complete induction) we get:
with lesser and the induction hypothesis
- .
algorithm
The multiplication of two natural numbers can be calculated using the following algorithm, where the radix (base) and the number of digits represent:
The algorithm is based on the fact that the individual digits of a number are multiplied by the other number and shifted. At the end the multiplied and shifted numbers are added.
Gaussian sum factor rule
When multiplying a number of arbitrary factors, the largest possible product is achieved if the total difference between the factors is as small as possible while the sum of the factors remains the same. The total difference is calculated by adding up all the differences between the factors.
- example
Product of three factors. The sum of the factors is 30.
As the total difference between the factors increases, the product (usually) becomes smaller.
Gesamtdifferenz 10 ∙ 10 ∙ 10 = 1000 0 ( 0 + 0 + 0 ) 9 ∙ 10 ∙ 11 = 990 4 ( 1 + 2 + 1 ) 8 ∙ 11 ∙ 11 = 968 6 ( 3 + 3 + 0 ) 8 ∙ 10 ∙ 12 = 960 8 ( 2 + 4 + 2 ) 7 ∙ 11 ∙ 12 = 924 10 ( 4 + 5 + 1 ) 7 ∙ 10 ∙ 13 = 910 12 ( 3 + 6 + 3 ) … 0 ∙ 1 ∙ 29 = 0 58 ( 1 + 29 + 28) 0 ∙ 0 ∙ 30 = 0 60 ( 0 + 30 + 30)
The Gaussian summation factor rule is equivalent to the statement that the content of a geometric figure is maximal when its sides have the same length. With the same circumference, the square is the rectangle with the largest area.
More or less than two factors
The product of more than two factors is defined by multiplying two factors starting from the left and continuing until only one number remains. The associative law now says that one can start at any point; also from the right. Due to the commutative law, the order is also irrelevant, so that you can start with any two factors (which do not have to be directly related to one another).
Even the product of a single factor or of no factors at all is defined, although you no longer have to multiply: the product of a number is this number itself, and the product of no factor is 1 (generally the neutral element of multiplication).
It is also possible to form an infinite product. The order of the factors plays a role here, however, so the factors can no longer be interchanged at will, and arbitrary combinations of partial products are not always possible. (Similar to infinite sums.)
Written multiplication
The basic idea behind written multiplication is:
- both factors are broken down into their digits,
- every digit of one factor is multiplied by every digit of the other factor
- all these partial results are added up.
The product of the two factors comes out as the total.
example
The written multiplication of the numbers 1234 and 5678 looks like this:
| 1 | 2 | 3 | 4th | * | 5 | 6th | 7th | 8th | ||||
| 2 | 2 | 7th | 1 | 2 | ||||||||
| + | 1 | 7th | 0 | 3 | 4th | |||||||
| + | 1 | 1 | 3 | 5 | 6th | |||||||
| + | 5 | 6th | 7th | 8th | ||||||||
| = | 7th | 0 | 0 | 6th | 6th | 5 | 2 |
The steps to get there are:
Write the numbers 1234 and 5678 next to each other in one line, separated by the multiplication symbol. A line is drawn under this line so that the task is clearly separated from the calculation steps.
| 1 | 2 | 3 | 4th | * | 5 | 6th | 7th | 8th |
The partial accounts come under this line. The first number (the multiplier) is broken down into its digits, and each of those digits is individually multiplied by the second number. This step is usually not written out and is only used here for understanding. If you add up all these partial results, the product comes out.
| 1 | 2 | 3 | 4th | * | 5 | 6th | 7th | 8th | ||||
| 4th | * | 5 | 6th | 7th | 8th | |||||||
| + | 3 | 0 | * | 5 | 6th | 7th | 8th | |||||
| + | 2 | 0 | 0 | * | 5 | 6th | 7th | 8th | ||||
| + | 1 | 0 | 0 | 0 | * | 5 | 6th | 7th | 8th | |||
| = | 7th | 0 | 0 | 6th | 6th | 5 | 2 |
The first of the partial calculations is still a multiplication, so it is further solved:
| 1 | 2 | 3 | 4th | * | 5 | 6th | 7th | 8th | ||||
| 4th | * | 8th | ||||||||||
| + | 4th | * | 7th | 0 | ||||||||
| + | 4th | * | 6th | 0 | 0 | |||||||
| + | 4th | * | 5 | 0 | 0 | 0 | ||||||
| + | 3 | 0 | * | 5 | 6th | 7th | 8th | |||||
| + | 2 | 0 | 0 | * | 5 | 6th | 7th | 8th | ||||
| + | 1 | 0 | 0 | 0 | * | 5 | 6th | 7th | 8th | |||
| = | 7th | 0 | 0 | 6th | 6th | 5 | 2 |
Now all that remains is multiplications of one digit by another digit. They are so simple that you either know them by heart or look them up in a small 1 × 1.
| 1 | 2 | 3 | 4th | * | 5 | 6th | 7th | 8th | ||||
| 3 | 2 | |||||||||||
| + | 2 | 8th | 0 | |||||||||
| + | 2 | 4th | 0 | 0 | ||||||||
| + | 2 | 0 | 0 | 0 | 0 | |||||||
| + | 3 | 0 | * | 5 | 6th | 7th | 8th | |||||
| + | 2 | 0 | 0 | * | 5 | 6th | 7th | 8th | ||||
| + | 1 | 0 | 0 | 0 | * | 5 | 6th | 7th | 8th | |||
| = | 7th | 0 | 0 | 6th | 6th | 5 | 2 |
The top lines of the addition are now summarized:
| 1 | 2 | 3 | 4th | * | 5 | 6th | 7th | 8th | ||||
| 2 | 2 | 7th | 1 | 2 | ||||||||
| + | 3 | 0 | * | 5 | 6th | 7th | 8th | |||||
| + | 2 | 0 | 0 | * | 5 | 6th | 7th | 8th | ||||
| + | 1 | 0 | 0 | 0 | * | 5 | 6th | 7th | 8th | |||
| = | 7th | 0 | 0 | 6th | 6th | 5 | 2 |
The remaining subtasks that have not yet been calculated are calculated in the same way.
| 1 | 2 | 3 | 4th | * | 5 | 6th | 7th | 8th | ||||
| 2 | 2 | 7th | 1 | 2 | ||||||||
| + | 1 | 7th | 0 | 3 | 4th | 0 | ||||||
| + | 1 | 1 | 3 | 5 | 6th | 0 | 0 | |||||
| + | 5 | 6th | 7th | 8th | 0 | 0 | 0 | |||||
| = | 7th | 0 | 0 | 6th | 6th | 5 | 2 |
The zeros to the right of the margin are usually not written in order to reduce the writing effort and because they have no effect on addition.
Multiplication with your fingers
Not only adding but also multiplying can be done to a limited extent with the fingers. To do this, both factors must be in the same half of the decade, i.e. either both end in digits from 1 to 5 or on digits from 6 to 0.
In the first case, the fingers are numbered starting with the little finger with 10 ( d -1) + 1 to 10 ( d -1) + 5 for the thumb, where d stands for the decade of the corresponding number (e.g. 11 to 15 for the second decade). Then you hold the two fingers whose product you want to calculate together. The corresponding product is obtained by counting the lower finger (the two together held finger count them) and d multiplied x 10, to the product of the lower finger of the left hand with the lower fingers of the right hand (each with jointly held fingers) and finally an additive constant ( d -1) 2 x 100 is added.
In the second case, the fingers are numbered from 10 · ( d -1) + 6 to 10 · d (e.g. 16 to 20). Then, as in the first case, hold the two fingers of the desired factors together, count the lower fingers, but now multiply them by d · 10 and add the product of the upper fingers (again without the fingers held together) to this, resulting in the additive constant turns out to be ( d -1) d 100.
- For example, to calculate 7 times 8, you count the lower fingers - here it's 5 - and multiply them by 10 ( d = 1). You get 50. Now you multiply the upper fingers of one hand - here 3 - by that of the other - here 2 - and you get 3 · 2 = 6. Now add the two intermediate results, so 50 + 6 = 56, and you get the final result. The additive constant ( d -1) d 100 is here 0 1 100 = 0.
- When you multiply 24 and 22 you count the lower fingers to 6, multiply this by 20 (( d -1) · 10 = 2 · 10) to 120, add the product of the lower fingers 4 · 2 = 8 and the additive constant ( d -1) ² x 100 = 400 and thereby obtains 528.
This method is particularly suitable for quickly calculating square numbers without a pocket calculator. This method can still be used for factors of different decades and halves of the decade by splitting the factors into sums.
The background to this process is the fact that such products can be written as:
and can calculate products of the second half of the decade by taking the complements of the last digit with respect to 10. The last digit is then the product of the complements, the tens the complement of the sum of the complements.
Vedic multiplication
This type of calculation comes from India and is part of so-called Vedic mathematics . In this computing system, the numbers are first analyzed and then a suitable method for calculating them is selected. For example B. a method which is always suitable for a “lightning” multiplication of even large factors when these are just below or above the same power of ten.
The calculation method is based on the following relationship: and are two numbers just below a power of ten and / or the differences between them. Then
If it is now , you can simply write the two digit sequences of and next to each other in order to arrive at the solution of the multiplication. (Attention: Leading zeros of the second term must be written.)
- Examples
95 ∙ 97 = 9215 992 ∙ 988 = 980096 12 ∙ 13 = 156 98 ∙ 102 = 9996
Fakt. Diff. Fakt. Diff. Fakt. Diff Fakt. Diff
a,b zu 100 a,b zu 1000 a,b zu 10 a,b zu 100
––––––––––––––– ––––––––––––––––– –––––––––––––– ––––––––––––––
95 -5 992 - 8 12 +2 98 - 2
\ ∙ \ ∙ \ ∙ \ ∙
97 -3 988 -12 13 +3 102 + 2
––––––––––––––– ––––––––––––––––– –––––––––––––– ––––––––––––––
92 15 980 096 15 6 99 96
(95-3)(-5∙-3) (992-12) (-8∙-12) (12+3) (3∙2) ( 98+2-1) (100+(-2)∙2) (97-5) (5∙3) (988- 8) (8∙12) (13+2) (3∙2) (102-2-1) (100-2∙2)
In the latter case, one number lies above and one below 100. Since in this case it is the product, a carryover has to be made from the left number, i.e. left , right .
Of course, swapping the factors gives the same result, since: is, see the last line of the example. Since the same signs always become + when multiplying two numbers, they can also be omitted for these cases, as indicated in the last line.
You can also use and as a basis . The calculation here is the same as for , except that it is calculated on the right or as a difference and multiplied by 2 on the left (base 20) or divided by 2 (base 50). For the base 50, if the sum on the left is odd, only the integer portion after division by 2 is used and added to the right as a carry . Proof to insert and transform accordingly .
Russian pawn multiplication
A and B are integral factors. The product P = A · B can also be determined in the following - seemingly curious - way:
- Step: Divide A and the results by 2 until the result is 1. A non-integer result is rounded down to the nearest whole number and then division by 2 is continued.
- Step: Double B continuously.
- Step: Delete all rows in which there is an even number in column A.
- Step: Add up all the numbers that have not been crossed out in column B. The sum obtained is the product you are looking for P.
Example: 11 3 =?
Spalte A Spalte B
11 · 3
5 6
2 12 gestrichen wegen (2 = gerade) in Spalte A
1 24
_______________________
Summe 33
Explanation
In column A, deletions are made, where the decimal number 11 in the binary representation contains zeros: 11 (decimal) = 1011 (binary). Column A should be read from bottom to top. This method is also the easiest way to transform decimal numbers into binary ones. The consecutive doublings in column B correspond to the powers of two of the binary number system, multiplied by the second factor. Where there is a zero in column A, the corresponding number in B is multiplied by 0 and therefore deleted. All other numbers in column B belong to the product and are added up.
You can easily formulate this differently.
The final equation is similar to the binary representation 1011 of FIG.
Multiplication with compasses and ruler
The set of chords can be used for graphical multiplication with a compass and ruler : A straight line is drawn through a point O and from O the lengths to be multiplied and in opposite directions are plotted. This creates two new points arise A and B . A second straight line is drawn through O. On this one carries from a range of length one, making another point E is produced. The second straight line is the circle through the points A , B and E in a point C cut. According to the chord set, the distance between O and C has the length you are looking for
The required circle can be constructed as a circumference around the triangle spanned by A , B and E. In addition to the set of chords, the set of secants is also useful for constructing the product of two numbers. When using the secant theorem, the starting point O lies outside the circle, and the quantities a and b are plotted in the same direction as seen from O. Correspondingly, when viewed from O , C then also lies in the same direction in which the one was removed.
Another possibility for graphical multiplication with compasses and ruler results from the theorem of rays . Here you first carry lines of lengths 1 and b on a beam with starting point A , both of which begin in A. Then from the end point E of the line of length 1 a line of length a is plotted and a second ray is drawn through its end point C and A , so that A is again the starting point of the ray. Then draw a straight line parallel to a through the end point B of segment b . Intersects the second beam in D . The length of the line BD corresponds to the product of a and b .
Generalizations
The well-known multiplication of real numbers can be generalized to multiply complex numbers of the form by using the distributive law :
By demanding some of the mathematical laws given above, one arrives at algebraic structures with two links, one addition and one multiplication. In a ring there is an addition, with which the set forms an Abelian group , and a multiplication, which is associative and distributive. If the multiplication has a neutral element, the ring is called unitary . If division is also always possible, you get an oblique body . If the multiplication is also commutative, one gets a field .
Not to be confused with this multiplication are other links which are commonly referred to as products, e.g. B. the scalar product in Euclidean vector spaces , the scalar multiplication in vector spaces, the matrix multiplication and the cross product in three-dimensional space . One speaks of multiplication also for size values of physical quantities.
See also
- Linear factor , prime factorization
- Schönhage Strassen algorithm , Karatsuba algorithm , Toom Cook algorithm
Web links
- Who actually invented multiplication? (PDF, 169 KiB)