rectangle

Rectangle with length a , width b and diagonal d

In geometry , a rectangle (an orthogon ) is a flat quadrangle whose interior angles are all right angles . It is a special case of the parallelogram and thus also of the trapezoid . A special case of the rectangle is the square , in which all sides are of the same length.

In topology , a rectangle is a manifold with a border, more precisely a manifold with corners.

properties

The following applies to the rectangle:

Opposite sides are the same length and parallel .
The four interior angles are the same, that is, it is an equiangular polygon . The interior angles are right angles .
The two diagonals are the same length and cut in half.
It has a circumference and is therefore a quadrilateral tendon . The center of the circumference is the intersection of the diagonals .
It is axially symmetrical with respect to the median perpendiculars of the sides. The two axes of symmetry are therefore perpendicular to one another.
It is point symmetric (twofold symmetric) with respect to the intersection of the diagonals.
The symmetry group is the Klein group of four .

The rectangle can be characterized as

Parallelogram with a right angle
Parallelogram with diagonals of equal length

Square with diagonals of equal length that cut in half

Formulas

The area of a rectangle is equal to the product of the side lengths.

Mathematical formulas for the rectangle
Area	${\ displaystyle A = a \ cdot b}$
scope	${\ displaystyle U = 2 \ times a + 2 \ times b = 2 \ times (a + b)}$
Length of the diagonal	${\ displaystyle d = {\ sqrt {a ^ {2} + b ^ {2}}}}$
Perimeter radius	${\ displaystyle r = {\ frac {1} {2}} \ cdot {\ sqrt {a ^ {2} + b ^ {2}}}}$
Interior angle	${\ displaystyle \ alpha = \ beta = \ gamma = \ delta = 90 ^ {\ circ}}$

The formula for the length of the diagonal is based on the Pythagorean theorem . The perimeter radius is obtained by halving the length of the diagonals.

To construct a rectangle, two sizes must be given. Often either one of the two side lengths and the length of the diagonal or both side lengths are given.

Golden rectangle

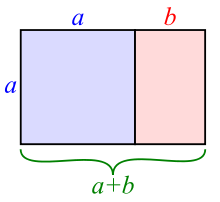
Both rectangles - each with the aspect ratios a: b and (a + b): a - are each golden rectangles ( animated representation ).

Rectangles with the property for the side lengths a and b are called golden rectangles . The aspect ratio is the golden ratio , so . ${\ displaystyle {\ frac {a + b} {a}} = {\ frac {a} {b}}}$ ${\ displaystyle {\ frac {a} {b}} = {\ frac {1 + {\ sqrt {5}}} {2}} \ approx 1 {,} 6180339887}$

Perfect rectangle

Perfect rectangle with sides 32 and 33

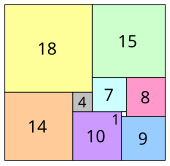
A rectangle is called perfect if it can be covered with squares without any gaps and without overlapping, whereby all squares are of different sizes. It is not easy to find such a tiling . Such a division of a rectangle with sides 32 and 33 into 9 squares was found in 1925 by Zbigniew Moroń . It consists of squares with sides 1, 4, 7, 8, 9, 10, 14, 15 and 18.