Symmetry group

Four regular polygons and two further geometric figures with all their symmetry elements, the key figures n of their rotational / rotational symmetry and their mirror symmetry axes (here n = 1 means: without rotational symmetry)

In mathematical group theory , the symmetry group of a geometric object is the group that consists of the set of all congruence maps that map the object to itself, together with the concatenation of mappings as a group operation .

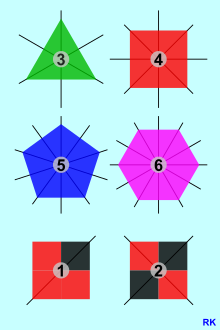
The graphic shows six two-dimensional symmetrical objects, namely four homogeneous regular polygons and two further geometric figures , with all of their symmetry elements being marked. The symmetry elements are properties of the figures. The totality of the symmetry elements of a figure forms its special symmetry group.

Rotational symmetry and mirror symmetry using examples

If you examine a geometrical figure for its symmetries, you can initially do without the mathematical term group . It may be beneficial if beginners in the field of symmetry groups stick to the approach of the mathematician, physicist and philosopher Hermann Weyl . Weyl, one of the pioneers of group theory, begins the foreword to his famous book Symmetrie as follows:

Starting with the somewhat vague notion of symmetry as the harmony of proportions, these four lectures first develop the concept of geometric symmetry in its various forms as bilateral, translative, rotative, ornamental and crystallographic symmetry and finally rise to the general, underlying all these forms Idea, namely the idea of the invariance of a structure in relation to a group of automorphic transformations.

A figure is rotationally symmetrical if it cannot be distinguished from the figure that results when it is rotated around a central point through the angle . A circle or a circular ring are rotationally symmetrical in the narrower sense. A rotation through any desired angle maps it onto itself. ${\ displaystyle \ varphi}$

A figure is also called rotationally symmetrical (or rotationally symmetrical) if it can be depicted on itself by rotating it around the central point by a fixed angle with 0 ° <<360 °. The angle of rotation can only be determined by dividing the full angle by a value produced> 1, ie . This number is a measure of rotational symmetry and is also called "count". Accordingly, this symmetry is also called -numerous or -fold rotational symmetry / rotational symmetry, in English " -fold rotational symmetry". The neutral symmetry operation is always included. This means “no operation”, ie the “operation” that leaves the figure in its original position. It is no different from turning the figure around . ${\ displaystyle \ varphi}$ ${\ displaystyle \ varphi}$ ${\ displaystyle n}$ ${\ displaystyle \ varphi = {\ frac {360 ^ {\ circ}} {n}}}$ ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle \ varphi = 360 ^ {\ circ}}$

Regular polygons are typical rotationally symmetrical figures. The graphic shows the first four, with the largest possible key figure of the rotational symmetry being drawn in the center. In addition, two further figures are shown, namely one without and one with double rotational symmetry. In the trivial case, there is no rotational symmetry / rotational symmetry and the code number 1 is not used in the mathematical context, unless you want to identify the trivial cyclic group , which only consists of the identical mapping . ${\ displaystyle n}$ ${\ displaystyle n = 1}$ ${\ displaystyle C_ {1}}$

A figure is mirror-symmetrical if it is mirrored on one of the mirror-symmetry axes and if it cannot be distinguished from the image it creates. All figures shown are mirror-symmetrical. They have 3, 4, 5, 6, 1 or 2 axes of mirror symmetry. Homogeneous regular polygons have as many mirror symmetry axes as they have rotational symmetry elements (if one counts the neutral symmetry operation among the rotational symmetry elements). The reverse does not apply: A figure with n-fold rotational symmetry does not necessarily need to have mirror symmetry axes. The following also applies: If a figure has a mirror symmetry axis, it does not necessarily have to be rotationally symmetrical, as the figure in the lower left corner of the graphic shows.

One arrives at the symmetry group of the respective figure by systematizing the symmetries of the respective figure, the respective object.

Disambiguation

A homogeneous tetrahedron is invariant to 12 different rotations. These are shown here as a cycle graph together with the rotations around the 180 ° edge (blue arrows) and the 120 ° vertices (reddish arrows). The 12 revolutions form the rotation group (symmetry group) of the figure. The coloring of the surfaces only serves to illustrate the symmetry operations, because a tetrahedron whose side surfaces are colored as in the graphic does not have any symmetries.

The following terms describe possible properties of an object, which can be used to determine which symmetry group the object belongs to.

Discreetness

A symmetry group has a discrete topology if there is such a thing as “smallest steps”. For example, a group of rotations about a point is discrete if and only if all possible angles of rotation are multiples of a smallest angle. On the other hand, if the group also contains any small angles of rotation, then this group is not discrete. In general, every group with a finite number of elements has a discrete topology. A discrete group can be described by a finite number of symmetry operations Composition produce . The reverse does not apply.

In practical terms, a symmetry group is discrete if and only if there is a lower bound , both for the lengths of all displacements (different from zero) and for the angles of rotation of all rotational symmetries.

periodicity

One considers the set of all displacements ( translations ) contained in the group (different from zero ) and determines how many of these vectors are linearly independent of one another, i.e. one determines the dimension of the linear envelope of these displacement vectors.

If the group does not contain any shifts at all, there is at least one point that is the fixed point of all mappings. In this case one speaks of a point group . Point groups are finite if and only if they are discrete.

As soon as the group contains at least one displacement, it automatically contains an infinite number of elements, at least in Euclidean geometry .

If the number of linearly independent displacement vectors corresponds to the dimension of the space in which the object is embedded, there is a limited part of the object (a cell ), the images of which fill the entire space. If the group is also discrete, one speaks of a space group and calls the pattern periodic . In this case there is a restricted fundamental domain of the same dimensions as space, for example a corresponding non-zero surface in the plane .

Two-dimensional Euclidean geometry

The symmetry groups in the Euclidean plane can be classified as follows:

Discreet
- Without shifts
  - Without axis reflections
    Family of finite cyclic groups (for ), that is, all rotations around a point by multiples of ${\ displaystyle C_ {n}}$ ${\ displaystyle n = 1,2, \ ldots}$ ${\ displaystyle {\ tfrac {360 ^ {\ circ}} {n}}}$
    
    ${\ displaystyle C_ {1}}$ : Symmetry group of a completely asymmetrical object, with the identity as the only element
    
    ${\ displaystyle C_ {2}}$ : Symmetry group of a point reflection
    
    ${\ displaystyle C_ {3}}$ : Symmetry group of a triskele
    
    ${\ displaystyle C_ {4}}$ : Symmetry group of a swastika
  - With axis reflections
    Family of dihedral groups (for ), these are rotations as if together with mirror axes through the center ${\ displaystyle D_ {n}}$ ${\ displaystyle n = 1,2, \ ldots}$ ${\ displaystyle C_ {n}}$ ${\ displaystyle n}$
    
    ${\ displaystyle D_ {1}}$ : Single axis mirroring
    
    ${\ displaystyle D_ {2}}$ : Symmetry group of a non-square rectangle , a non-square diamond (D2 is isomorphic to Klein's group of four )
    
    ${\ displaystyle D_ {n}}$ : Symmetry group of a regular n corner
- With displacements that are all collinear (span of translations has rank 1)
  7 frieze groups
- With at least two linearly independent shifts
  17 planar crystallographic groups
Not discreet
- Without shifts
  Orthogonal group , these are all symmetries of a circle, i.e. all rotations and all reflections on axes that go through the center ${\ displaystyle O (2)}$
- With shifts
  This case still needs to be broken down.

Other dimensions

Three-dimensional point groups are classified in detail in a separate article.
The article on room groups also goes into different dimensions.

literature

Willard Miller, Jr .: Symmetry Groups and Their Applications . Academic Press, New York, London 1972, ISBN 0-12-497460-0 (x, 432, [1] ). This introductory textbook covers those aspects of group theory that are useful in the natural sciences without sacrificing mathematical rigor.
MS Dresselhaus: Group Theory - Application to the Physics of Condensated Matter. Springer Verlag, Heidelberg 2008, ISBN 978-3-54032-897-1
Michael Tinkham: Group Theory and Quantum Mechanics. Dover Pubn Inc - January 1, 2004, ISBN 978-0-48643-247-2

Individual evidence

↑ Hermann Weyl : Symmetrie: Supplemented by the text “Symmetry and Congruence” from the estate and with comments by Domenico Giulini, Erhard Scholz and Klaus Volkert. Translator Lulu Hofmann Bechtolsheim . 3. Edition. Springer Spectrum, Berlin, Heidelberg 2017, ISBN 978-3-662-52711-5 (VII, 232, limited preview in the Google book search [accessed on July 23, 2019]). Reprint of the original from 1952 in Hermann Weyl: Symmetry . Princeton University Press, Princeton, NJ 2015 (176 pp., Limited preview in Google Book Search [accessed July 23, 2019]).
↑ Weyl calls the mirror symmetry and bilateral symmetry (s. Bilaterality ), which is a bilateral symmetry , because a mirror symmetry plane divides a figure into two equal or an animal in two outwardly similar looking mirror-image halves. In the animal kingdom, bilaterality is the typical form of symmetry in the body . Around 95 percent of the multicellular animal species belong to the Bilateria , the "two-sided animals".
↑ rotational symmetry. Retrieved November 20, 2019 .
↑ symmetry. Retrieved June 20, 2019 .

Web links

Commons : Symmetry - collection of images, videos and audio files

[Weyl_1952-1] Hermann Weyl : Symmetrie: Supplemented by the text “Symmetry and Congruence” from the estate and with comments by Domenico Giulini, Erhard Scholz and Klaus Volkert. Translator Lulu Hofmann Bechtolsheim . 3. Edition. Springer Spectrum, Berlin, Heidelberg 2017, ISBN 978-3-662-52711-5 (VII, 232, limited preview in the Google book search [accessed on July 23, 2019]). Reprint of the original from 1952 in Hermann Weyl: Symmetry . Princeton University Press, Princeton, NJ 2015 (176 pp., Limited preview in Google Book Search [accessed July 23, 2019]).

[2] Weyl calls the mirror symmetry and bilateral symmetry (s. Bilaterality ), which is a bilateral symmetry , because a mirror symmetry plane divides a figure into two equal or an animal in two outwardly similar looking mirror-image halves. In the animal kingdom, bilaterality is the typical form of symmetry in the body . Around 95 percent of the multicellular animal species belong to the Bilateria , the "two-sided animals".

[3] rotational symmetry. Retrieved November 20, 2019 .

[4] symmetry. Retrieved June 20, 2019 .