Flat crystallographic group

The flat crystallographic groups , also called wall pattern groups or ornament groups , are the symmetry groups of periodic patterns or tiling of the Euclidean plane . There are, apart from affine equivalence, exactly 17 such groups. The 230 crystallographic space groups correspond to them in three-dimensional space .

In the sense of group theory , the groups consist of the set of all congruence maps that map the pattern onto itself, together with the composition of maps as a group operation .

Symmetry elements

A periodic pattern can have combinations of the following elementary symmetry elements:

1. Translation (displacement)
2. Axis mirroring
3. Glide mirroring , i.e. a combination of translation and axis mirroring
4. rotation
   • 2-digit, i.e. a rotation by 180 ° or a point reflection
   • 3-digit, i.e. a rotation of 120 °
   • 4 digits, i.e. a rotation of 90 °
   • 6 digits, i.e. a rotation of 60 °

Rotations other than those listed are impossible. This is because (apart from the twofold rotation) each symmetry group has a periodic tiling of the plane with regular polygons of corresponding numbers. And tiling with pentagons, for example, is impossible because the sum of the interior angles results in an interior angle of 108 °, so that such tiling would not open at the corners. In non-Euclidean geometries, however, symmetry groups with other numerals are also possible.

A 4-digit rotational symmetry naturally implies a 2-digit, just as a 6-digit implies both a 3-digit and a 2-digit. Usually only the highest value is given for each center of rotation.

Any periodic pattern can be generated by repeating these operations on a constrained unit cell until the entire plane is tiled. By definition, the symmetry group of a periodic pattern always contains two linearly independent translations. This also makes it possible to generate the entire pattern simply by repeatedly shifting a translative cell. The translative cell contains one or more copies of the elementary cell.

notation

Orbifold notation

The properties of a symmetry group can also be described by the so-called orbifold notation.

• Numbers n (2, 3, 4, 6) denote an n -fold center of rotation.
• An ∗ stands for a mirror axis.
  • Numbers in front of an ∗ are off the mirror axes
  • Numbers that come after an ∗ are on the mirror axes
• An × stands for a sliding reflection.
• A ∘ stands for no symmetries apart from the translations
• The translations occurring in each group are not explicitly noted.

Brief overview

group	Orbifold notation	Translational cell (e.g.)	Unit cells in minimal translation cell
p1	∘1	parallelogram	1
p2	2222	parallelogram	2
pm	**	rectangle	2
pg	×θ	rectangle	2
cm	∗ ×	Rhombus	2
pmm	∗ 2222	rectangle	4 rectangles
pmg	22 ∗	rectangle	4th
pgg	22 ×	rectangle	4th
cmm	2 * 22	Rhombus	4th
p4	442	square	4th
p4m	∗ 442	square	8 right-angled isosceles triangles
p4g	4 ∗ 2	square	8th
p3	333	Diamond made up of two equilateral triangles	3
p3m1	∗ 333	Diamond made up of two equilateral triangles	6 equilateral triangles
p31m	3 ∗ 3	Diamond made up of two equilateral triangles	6th
p6	632	Diamond made up of two equilateral triangles	6th
p6m	∗ 632	Diamond made up of two equilateral triangles	12 right triangles with a side ratio of 2: 1

list

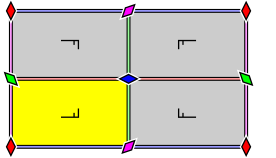
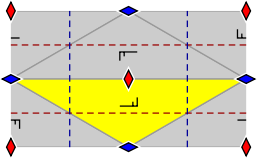
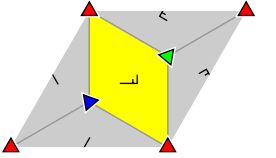
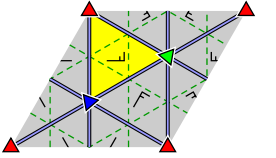
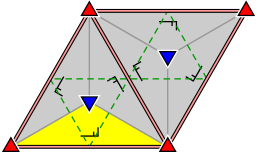
The elements indicated in the structure diagrams are identified as follows:

	Center of a twofold rotation (180 °).
	Center of a threefold rotation (120 °).
	Center of a fourfold rotation (90 °).
	Center of a six-fold rotation (60 °).
	Mirror axis.
	Glide axis.

Different equivalence classes of the elements are identified by different colors and rotations.

The area marked in yellow indicates a unit cell, the entire area shown is a translative cell.

Group p1

Classes of symmetry elements in p1

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
-	-	-	-	-	-

• Orbifold notation: ∘1 .
• This group has only displacement as the only form of symmetry.

Group p2

Classes of symmetry elements in p2

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
4th	-	-	-	-	-

• Orbifold notation: 2222 .
• This group has four classes of point mirror centers. This twofold rotation is the only form of symmetry besides translation.

Group pm

Classes of symmetry elements in pm

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
-	-	-	-	2	-

• Orbifold notation: ∗∗ .
• This group has two mirror axes parallel to each other. There is no rotational symmetry.

Group pg

Classes of symmetry elements in pg

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
-	-	-	-	-	2

• Orbifold notation: ×phia .
• This group has two parallel sliding mirror axes. There is no rotational symmetry.

Group cm

Classes of symmetry elements in cm

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
-	-	-	-	1	1

• Orbifold notation: ∗ × .
• This group has alternating mirror axes and sliding mirror axes parallel to one another.

Group pmm

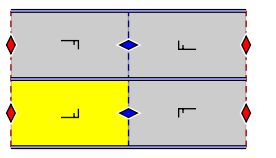
Classes of symmetry elements in pmm

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
4th	-	-	-	4th	-

• Orbifold notation: ∗ 2222 .
• This group is characterized by mutually perpendicular mirror axes. Twofold centers of rotation result at the intersection of two mirror axes. There are a total of four classes of turning centers and four classes of mirror axes.

Group pmg

Classes of symmetry elements in pmg

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
2	-	-	-	1	2

• Orbifold notation: 22 ∗ .
• There is a single class of mirror axes as well as two different classes of glide mirror axes perpendicular to them, on which twofold centers of rotation arise.

Group pgg

Classes of symmetry elements in pgg

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
2	-	-	-	-	2

• Orbifold notation: 22 × .
• This group does not have a simple axis symmetry, but has two mutually perpendicular sliding mirror axes and two classes of point mirror centers.

Group cmm

Classes of symmetry elements in cmm

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
3	-	-	-	2	2

• Orbifold notation: 2 ∗ 22 .
• This group contains two classes of mirror axes, which are perpendicular to each other, with twofold centers of rotation at the points of intersection. An additional class of twofold turning centers lies apart from the mirror axes. This also leads to two classes of sliding mirror axes.

Group p4

Classes of symmetry elements in p4

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
1	-	2	-	-	-

• Orbifold notation: 442 .
• This group has no form of axial symmetry. The distinguishing feature are fourfold rotations, for which there are two classes of centers. In between there are twofold turning centers.

Group p4m

Classes of symmetry elements in p4m

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
1	-	2	-	3	1

• Orbifold notation: ∗ 442 .
• This group is also known as p4mm .

Group p4g

Classes of symmetry elements in p4g

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
1	-	1	-	1	2

• Orbifold notation: 4 ∗ 2 .
• This group is also known as p4gm .

Group p3

Classes of symmetry elements in p3

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
-	3	-	-	-	-

• Orbifold notation: 333 .

Group p3m1

Classes of symmetry elements in p3m1

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
-	3	-	-	1	1

• Orbifold notation: ∗ 333 .

Group p31m

Classes of symmetry elements in p31m

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
-	2	-	-	1	1

• Orbifold notation: 3 ∗ 3 .

Group p6

Classes of symmetry elements in p6

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
1	1	-	1	-	-

• Orbifold notation: 632 .

Group p6m

Classes of symmetry elements in p6m

Rotations				axes
2	3	4th	6th	Mirror-	Glide mirror
1	1	-	1	2	2

• Orbifold notation: ∗ 632 .
• This group is also known as p6mm .

Ornamental groups in art

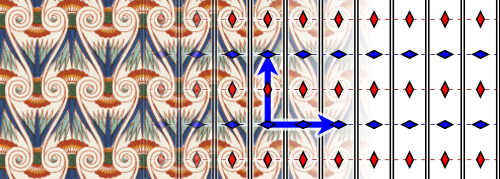
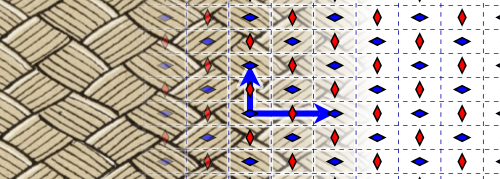
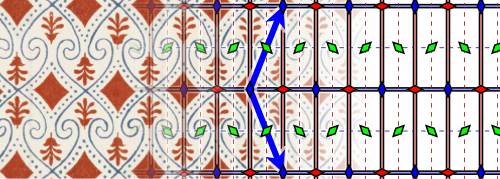
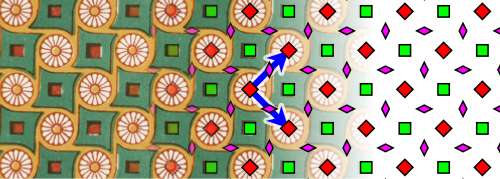
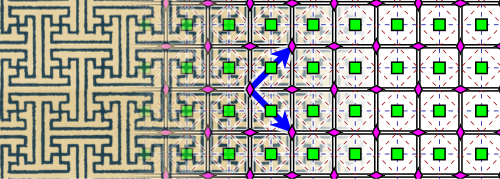
In the case of double periodic patterns from ancient Egypt , 12 of the 17 ornament groups were detected; the 5 groups with 3 or 6-fold rotational symmetry are missing. The arabesques in the Alhambra are considered an excellent example of the use of double periodic patterns in Islamic art . Whether or not all 17 ornament groups appear in the Alhambra is controversial: Edith Müller and Branko Grünbaum say no, José María Montesinos and Marcus du Sautoy say yes. With the possible exception of pm, p3 and pg, all ornament groups were used in China .

See also

• Symmetry (geometry)
• Point group

literature

• Branko Grünbaum , Geoffrey C. Shephard: Tilings and Patterns. Freeman, New York NY 1987, ISBN 0-7167-1193-1 .
• Michael Klemm: Symmetries of Ornaments and Crystals. Springer, Berlin et al. 1982, ISBN 3-540-11644-3 .
• Klaus Lamotke: The symmetry groups of the plane ornaments . In: Mathematical semester reports . tape 52 , no. 2 , August 2005, p. 153-174 , doi : 10.1007 / s00591-005-0092-y .

Individual evidence

1. ^ Branko Grünbaum: The Emperor's New Clothes: Full Regalia, G string, or Nothing? In: The Mathematical Intelligencer. Vol. 6, No. 4, 1984, pp. 47-53, doi : 10.1007 / BF03026738 .
2. ↑ Edith Müller: Group-theoretical and structural analysis of the Moorish ornaments from the Alhambra in Granada. Baublatt, Rüschlikon 1944 (at the same time: Zurich, university, dissertation, 1944).
3. ^ Branko Grünbaum: What Symmetry Groups Are Present in the Alhambra? In: Notices of the American Mathematical Society. Vol. 53, No. 6, 2006, ISSN  0002-9920 , pp. 670-673, digital version (PDF; 1.97 MB) .
4. ^ José M. Montesinos: Classical Tesselations and Three-Manifolds. Springer, Berlin et al. 1987, ISBN 3-540-15291-1 .
5. ↑ Marcus du Sautoy : Finding Moonshine. A Mathematician's Journey through Symmetry. Fourth Estate, London 2008, ISBN 978-0-00-721461-7 , chapter 3.
6. ^ Doris Schattschneider : The Plane Symmetry Groups: Their Recognition and Notation. In: The American Mathematical Monthly. Vol. 85, No. 6, 1978, pp. 439-450, doi : 10.2307 / 2320063 .

Web links

Commons : Symmetry  - collection of images, videos and audio files

• morenaments euc , Java Applet and Application. Retains drawn lines when changing groups.
• Escher Web Sketch , Java Applet. In addition to freehand drawing, it also allows the use of individual other objects.