parallelogram

A parallelogram (from ancient Greek παραλληλό-γραμμος paralleló-grammos "bounded by two pairs of parallels") or rhomboid (diamond-like) is a convex, flat square with opposite sides parallel .

Parallelograms are special trapezoids and two-dimensional parallelepipeds . Rectangle , diamond (rhombus) and square are special cases of the parallelogram.

properties

A square is a parallelogram if and only if one of the following conditions is met:

• Opposite sides are of the same length and no two opposite sides intersect (no overturned square, so-called antiparallelogram ).
• Two sides are parallel and of equal length.
• Opposite angles are the same size.
• Any two adjacent angles add up to 180 °.
• The diagonals bisect each other.
• The sum of the areas of the squares over the four sides is equal to the sum of the areas of the squares over the two diagonals ( parallelogram equation ).
• It is point symmetric (twofold rotationally symmetric ).

The following applies to every parallelogram:

• Each diagonal divides it into two triangles that are congruent in the same direction .
• Its center of symmetry is the intersection of the diagonals .
• The centers of the squares erected over its sides form a square ( theorem of Thébault-Yaglom ).

All parallelograms that have at least one axis of symmetry are rectangles or diamonds .

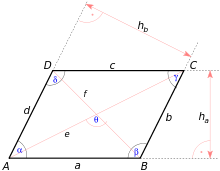
Formulas

Mathematical formulas for the parallelogram
Area	${\displaystyle A=a\cdot h_{a}=b\cdot h_{b}=\left|\left|{\overrightarrow {AB}}\times {\overrightarrow {AD}}\right|\right|}$ ${\displaystyle A=a\cdot b\cdot \sin(\alpha )=a\cdot b\cdot \sin(\beta )={\frac {e\cdot f\cdot \sin(\theta )}{2}}}$ Via transformation into a rectangle with the determinant : ${\displaystyle A=\det {\begin{pmatrix}a_{x}&&b_{x}\\a_{y}&&b_{y}\end{pmatrix}}=a_{x}\cdot b_{y}-b_{x}\cdot a_{y}}$
scope	${\displaystyle U=2\cdot a+2\cdot b=2\cdot (a+b)}$
Interior angle	${\displaystyle \alpha =\gamma ,\quad \beta =\delta ,\quad \alpha +\beta =180^{\circ }}$
height	${\displaystyle h_{a}=b\cdot \sin(\alpha )}$
	${\displaystyle h_{b}=a\cdot \sin(\beta )}$
Length of the diagonal (see cosine law )	${\displaystyle {\begin{array}{ccl}e&={\sqrt {a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos(\beta )}}\\&={\sqrt {a^{2}+b^{2}+2\cdot a\cdot b\cdot \cos(\alpha )}}\end{array}}}$
	${\displaystyle {\begin{array}{ccl}f&={\sqrt {a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos(\alpha )}}\\&={\sqrt {a^{2}+b^{2}+2\cdot a\cdot b\cdot \cos(\beta )}}\end{array}}}$
Interior angle	${\displaystyle \alpha =\gamma ,\quad \beta =\delta ,\quad \alpha +\beta =180^{\circ }}$
Parallelogram equation	${\displaystyle e^{2}+f^{2}=2\cdot (a^{2}+b^{2})}$

Proof of the area formula for a parallelogram

Six partial areas are subtracted from the large rectangle

Animation for calculating the area of a parallelogram. The area is equal to the product of the length of a base side and the associated height . ${\displaystyle b}$ ${\displaystyle h}$

The area of the adjacent black parallelogram can be obtained by subtracting the six small areas with colored edges from the area of ​​the large rectangle . Because of the symmetry and the interchangeability of the multiplication , you can also subtract twice the three small areas below the parallelogram from the large rectangle. So it is: ${\displaystyle A}$

${\displaystyle {\begin{array}{cccl}A&=&&(\color {YellowOrange}a_{x}\color {black}+\color {ForestGreen}b_{x}\color {black})\cdot (\color {red}a_{y}\color {black}+\color {blue}b_{y}\color {black})-2\cdot (\color {YellowOrange}a_{x}\color {black}\cdot \color {red}a_{y}\color {black}/2+\color {ForestGreen}b_{x}\color {black}\cdot \color {red}a_{y}\color {black}+\color {ForestGreen}b_{x}\color {black}\cdot \color {blue}b_{y}\color {black}/2)\\&=&&\color {YellowOrange}a_{x}\color {black}\cdot \color {red}a_{y}\color {black}+\color {YellowOrange}a_{x}\color {black}\cdot \color {blue}b_{y}\color {black}+\color {ForestGreen}b_{x}\color {black}\cdot \color {red}a_{y}\color {black}+\color {ForestGreen}b_{x}\color {black}\cdot \color {blue}b_{y}\\&&\color {black}-&\color {YellowOrange}a_{x}\color {black}\cdot \color {red}a_{y}\color {black}\quad \quad \quad -2\cdot \color {ForestGreen}b_{x}\color {black}\cdot \color {red}a_{y}\color {black}-\color {ForestGreen}b_{x}\color {black}\cdot \color {blue}b_{y}\\&=&&\quad \quad \quad \quad \color {YellowOrange}a_{x}\color {black}\cdot \color {blue}b_{y}\color {black}-\color {ForestGreen}b_{x}\color {black}\cdot \color {red}a_{y}\end{array}}}$

Construction of a parallelogram

A parallelogram, wherein the side lengths and as well as the height is given, is provided with ruler and compass constructible . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle h_{a}}$

Parallelogram with the given side lengths and and the height . The point can be freely selected for the construction of the right angle . Animation with a pause of 10 s at the end. ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle h_{a}}$ ${\displaystyle E}$

Generalizations

Parallelepiped

A generalization to dimensions is the parallelotope , explained as the set and its parallel displacements . They are linearly independent vectors . Parallelotopes are point symmetrical . ${\displaystyle n}$ ${\displaystyle \{\alpha _{1}\cdot p_{1}+\alpha _{2}\cdot p_{2}+\dotsb +\alpha _{n}\cdot p_{n}\mid 0\leq \alpha _{i}\leq 1\}}$ ${\displaystyle p_{i}}$ ${\displaystyle n}$

The three-dimensional parallelotope is the parallelepiped . Its side surfaces are six parallelograms that are congruent in pairs and lie in parallel planes . A parallelepiped has twelve edges, four of which are parallel and of equal length, and eight corners in which these edges converge at a maximum of three different angles .

Use in technology

Parallelograms are often found in mechanics. A movable, true-to-parallel mounting, the so-called parallelogram guide, can be created by four joints . Examples:

• 

  Switching parallelogram of a derailleur system

• 

  Parallel wipers

• 

  Aerial work platform

• 

  pantograph

literature

• F. Wolff: Textbook of Geometry. Fourth improved edition, printed and published by G. Reimer, Berlin 1845 ( online copy ).
• P. Kall: Linear Algebra for Economists. Springer Fachmedien, Wiesbaden 1984, ISBN 978-3-519-02356-2 .
• Wilhelm Killing: Textbook of Analytical Geometry. Part 2, Outlook Verlagsgesellschaft, Bremen 2011, ISBN 978-3-86403-540-1 .

Web links

Commons : Parallelogram  - collection of images, videos and audio files

Wiktionary: Parallelogram  - explanations of meanings, word origins, synonyms, translations

Wiktionary: Rhomboid  - explanations of meanings, word origins, synonyms, translations

• Eric W. Weisstein : Parallelogram . In: MathWorld (English).
• Area and circumference calculation of general and special parallelograms. ( Memento from January 11, 2015 in the Internet Archive ). Retrieved November 18, 2016.
• Introduction to the subject of the parallelogram. (PDF; 920 kB). Retrieved November 18, 2016.
• Parallelogram and diamond. ( Memento from November 19, 2016 in the Internet Archive ; PDF; 225 kB). Retrieved November 18, 2016.