square
In geometry , a square is a special polygon , namely a flat, convex and regular quadrilateral . It has four sides of equal length and four right angles . The square is a special case of the rectangle , the diamond , the parallelogram , the trapezoid and the dragon square . For the construction of a square, an indication is sufficient, e.g. B. the length of the side or the diagonal .
Squares are the faces of a platonic solid , namely the cube . The square is also the basic form of a platonic tiling . As a special case of corresponding general n -dimensional bodies , the square is both the two-dimensional hypercube and the two-dimensional cross polytope .
properties
The following applies to the square:
- The four sides are the same length, that is, it is a diamond and an equilateral polygon .
- The four interior angles are the same, that is, it is a rectangle and an equiangular polygon . The interior angles are right angles .
- The two diagonals are the same length, bisect each other and are orthogonal .
- The intersection of the diagonal is within - and incentre and center of symmetry . The square is both a chord and a tangent square .
- The area of the circumference is twice as large as that of the inscribed circle .
- It has 4 axes of symmetry : the two verticals and the two diagonals .
- It is four-fold rotationally symmetrical and therefore also point symmetrical .
- The symmetry group is the dihedral group .
The square can be characterized as
- Rectangle with two adjacent sides of equal length
- Diamond with two adjacent equal angles
- Diamond with a right angle
- Parallelogram with two adjacent sides of equal length and two adjacent equal angles
- Parallelogram with two adjacent sides of equal length and a right angle
- Square with orthogonal diagonals bisecting each other
Formulas
| Math formulas squared | ||
|---|---|---|
| Area | ||
| scope | ||
| Length of the diagonal | ||
| Inscribed radius | ||
| Perimeter radius | ||
| Interior angle | ||
construction
The square is a regular polygon that can be constructed with a compass and ruler .
Construction with a given side length
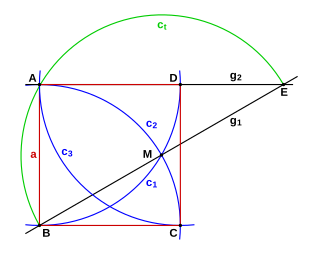
- Given: The side a with the endpoints A and B.
- Draw an arc around end A (c 1 , at least a quarter circle) with the side length as the radius.
- Draw an arc around end B (c 2 , at least a quarter circle) with the side length as the radius. The intersection of the circles is point M.
- Draw a straight line through points B and M (at least twice as long as BM )
- Draw a Thales circle (c t ) around M through B. You get point E.
- Draw a straight line through points A and E. The point of intersection with c 1 is corner D of the later square.
- Draw around D of the one arc (c 3 ) with the side length as the radius. The intersection with c 2 is corner C.
- Connect the corners to form a square.
Construction with a given diagonal
- Given: The diagonal d with the endpoints A and C.
- Construct the vertical line (blue) on the diagonal. The point of intersection with the diagonal is the center point M.
- Draw a circle around M through A. The intersection points with the perpendicular are the two missing corners B and D.
- Connect corners A, B, C, and D cyclically.
Animations
Tiling with squares
Some Platonic and Archimedean tiling contain squares. These tiling are periodic, rotationally symmetrical and translationally symmetrical and contain only regular polygons .
The numbers below the figures indicate how many corners the regular polygons have, each of which meets at a point . The interior angles add up to 360 °.
Polyhedron with squares
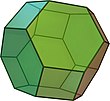
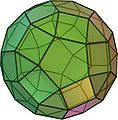
The cube is the only Platonic solid that has square faces . Some Archimedean solids also contain squares, for example the cuboctahedron , the truncated octahedron , the rhombic cuboctahedron, and the rhombicosidodecahedron .
Generalizations
In Euclidean geometry , the square is the two-dimensional special case of hypercube and cross polytope .
The term square is in the synthetic geometry of affine plane generalized by one of the equivalent statements that describe a square in the elementary geometry is used for the definition of the term. For example, for pre-Euclidean levels, the existence of these figures becomes an additional axiom .
In non-Euclidean geometries , squares are generally polygons with 4 sides of equal length and equal interior angles .
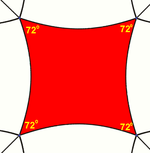
In spherical geometry , a square is a polygon whose sides are great circles that intersect at the same angle . In contrast to squares of planar geometry , the angles of a spherical square are larger than a right angle . Larger spherical squares have larger angles.
In hyperbolic geometry, there are no squares with right angles . Instead, squares have angles that are smaller than a right angle. Larger hyperbolic squares have smaller angles.
| Generalizations of the square | ||||
|---|---|---|---|---|
| geometry | spherical geometry | spherical geometry | Euclidean geometry | hyperbolic geometry |
| Interior angle | 180 ° | 120 ° | 90 ° | 72 ° |
| Schäfli symbol | {4, 2} | {4, 3} | {4, 4} | {4, 5} |
| Number of squares in the tiling | 2 | 6th | infinite | infinite |

|

|

|
|
|
Latin square
A Latin square is a square scheme with n rows and columns, each field being occupied by one of n different symbols, so that each symbol occurs exactly once in each row and in each column. The natural number n is called the order of the Latin square.
Examples
Magic square
A magic square with edge length n is a square arrangement of the natural numbers 1, 2,…, n², in which the sums of the numbers of all rows, columns and the two diagonals are the same. This sum is known as the magic number of the magic square.
Squaring the square
The squaring of the square is the tiling of a given square with smaller squares whose side lengths have integer values. The following additional conditions make the task interesting and demanding:
- No two sub-squares should be the same size. A square tiling that meets this requirement is called perfect .
- If a subset of the sub- squares forms a rectangle , the quadrature is called composite , otherwise simple .
Squaring the circle
Squaring the circle is a classic problem in geometry. The task is to construct a square with the same area from a given circle in finitely many steps . It is equivalent to the so-called rectification of the circle , i.e. the construction of a straight line that corresponds to the circumference of the circle. This in turn corresponds to the construction of the circle number from the segment 1. If one restricts the construction means to ruler and compass , the task is unsolvable due to the transcendence of . This could be proven in 1882 by the German mathematician Ferdinand von Lindemann .