Inscribed circle

Tangent pentagon with inscribed circle

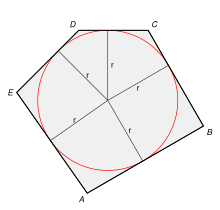
The inscribed circle of a polygon (polygon) in the Euclidean plane is the circle that touches all sides of the polygon in its interior (that is, it touches the lines between the corner points and not their extensions). It is also the largest circle that completely lies within the given polygon.

Only those polygons in which all bisectors of the interior angles of the polygons intersect at one point have an inscribed circle. In this case, the intersection is the center of the inscribed circle.

If the inscribed circle of a polygon exists with area and perimeter , the inscribed radius has the value ${\displaystyle A}$ ${\displaystyle u}$

${\displaystyle r={\frac {2A}{u}}}$.

Inscribed circle of a triangle

Triangle with inscribed circle

The inscribed circle is particularly important in triangular geometry . Every triangle has an inscribed circle, its center point lies at the intersection of the three bisectors. If you draw a circle around this point of intersection that touches one side of the triangle (the side becomes a tangent to the inscribed circle), this circle also touches the other two sides.

All points of the bisector of the interior angle have the same distance from the sides and . Accordingly, the points of the bisector of have the same distance from and . The intersection of these two bisectors has the same distance from all three sides of the triangle ( , and ). So it must also be on the third bisector. ${\displaystyle \alpha =\angle BAC}$ ${\displaystyle [AB]}$ ${\displaystyle [CA]}$ ${\displaystyle \beta =\angle CBA}$ ${\displaystyle [BC]}$ ${\displaystyle [AB]}$ ${\displaystyle [AB]}$ ${\displaystyle [BC]}$ ${\displaystyle [CA]}$

The inscribed circle touches all three sides from the inside - in contrast to the three circles , which touch one side from the outside and the extensions of the other two sides.

The inscribed center point, i.e. the intersection of the bisector, is one of the most prominent points of the triangle. He bears the Kimberling number . ${\displaystyle X_{1}}$

radius

If the area of the triangle with the sides is , and , then the radius of the inscribed circle is calculated by: ${\displaystyle A}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle r}$

${\displaystyle r={\frac {2A}{a+b+c}}={\sqrt {\frac {(s-a)(s-b)(s-c)}{s}}}}$

With

${\displaystyle s={\frac {a+b+c}{2}}={\frac {u}{2}}}$

The formula from Heron's theorem was used to calculate the area of the triangle . ${\displaystyle A}$

Depending on the given parameters of the triangle, the following relationship is interesting:

${\displaystyle r={\frac {a}{\cot \left({\frac {\beta }{2}}\right)+\cot \left({\frac {\gamma }{2}}\right)}}={\frac {b}{\cot \left({\frac {\alpha }{2}}\right)+\cot \left({\frac {\gamma }{2}}\right)}}={\frac {c}{\cot \left({\frac {\alpha }{2}}\right)+\cot \left({\frac {\beta }{2}}\right)}}}$

Coordinates

The Cartesian coordinates of the inscribed center are calculated as the mean of the corner coordinates weighted with the lengths of the opposite sides. If the three corner points are at , and , and the sides opposite the corner points have the lengths , and , then the in-circle center point is at ${\displaystyle (x_{A}/y_{A})}$ ${\displaystyle (x_{B}/y_{B})}$ ${\displaystyle (x_{C}/y_{C})}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle I(x_{I}/y_{I})}$ ${\displaystyle \left({\frac {ax_{A}+bx_{B}+cx_{C}}{a+b+c}}/{\frac {ay_{A}+by_{B}+cy_{C}}{a+b+c}}\right)}$

Coordinates in barycentric coordinates : , ${\displaystyle (a:b:c)}$

Coordinates in trilinear coordinates : . ${\displaystyle (1:1:1)}$

Other properties

• The distance between corner A and one of the adjacent contact points of the inscribed circle is the same ; here means half the circumference , as above. The same applies to the vertices B and C . ${\displaystyle s-a}$ ${\displaystyle s}$
• The straight lines connecting the corners of the triangle with the opposite contact points of the inscribed circle intersect at a point, the Gergonne point .
• The principle of the trident creates a connection between the circumference and the incircle.

Inscribed circle of a right triangle

If there is a right-angled triangle in the Euclidean plane, more detailed information can be given about the inscribed circle of such a triangle.

Radius of the inscribed circle

In the case of a right-angled triangle with side lengths , and , where the length of the hypotenuse is supposed to be, two simple equations can be given for the inscribed radius , which are as follows: ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle r}$

${\displaystyle r={\frac {a\cdot b}{a+b+c}}={\frac {a+b-c}{2}}}$.

Area formula

The point of tangency where the inscribed circle of the hypotenuse touched , this decomposed into partial stretch with the lengths

${\displaystyle x=a-r}$

and

${\displaystyle y=b-r}$.

This then applies with regard to the area of the right-angled triangle ${\displaystyle A}$

${\displaystyle A={\frac {a\cdot b}{2}}=(a-r)\cdot (b-r)=x\cdot y}$.

Incircles of other polygons

While there is always an inscribed circle with triangles, this only applies in special cases to polygons with more than three corners.

Quadrilaterals that have an inscribed circle are called tangent quadrilaterals . They include all convex dragon squares , especially all rhombuses and squares .

Regular polygons always have an inscribed circle, regardless of the number of corners. The following applies to the incircle radius of a regular corner with side length : ${\displaystyle n}$ ${\displaystyle a}$

${\displaystyle r={\frac {a}{2}}\cot {\tfrac {180^{\circ }}{n}}={\frac {a}{2\tan {\frac {180^{\circ }}{n}}}}}$

See also

• Radius
• Circle
• Circles on the triangle
• Incugel

literature

• Claudi Alsina, Roger B. Nelsen: Enchanting Evidence: A Journey Through the Elegance of Mathematics . Springer Spectrum, Berlin (among others) 2013, ISBN 978-3-642-34792-4 .
• HSM Coxeter , SL Greitzer: Timeless geometry. Klett, Stuttgart 1983, ISBN 3-12-983390-0 .
• Max Koecher , Aloys Krieg : level geometry. 3rd, revised and expanded edition. Springer-Verlag, Berlin a. a. 2007, ISBN 978-3-540-49327-3 .

Web links

Wiktionary: Inkreis  - explanations of meanings, word origins, synonyms, translations

• Walter Fendt: The inscribed circle of a triangle is drawn step by step
• Eric W. Weisstein : Inkreis . In: MathWorld (English).
• Flash animation for the incircle construction of the triangle (dwu teaching materials)

Individual evidence

1. ^ Claudi Alsina, Roger B. Nelsen: Enchanting Evidence: A Journey Through the Elegance of Mathematics. 2013, pp. 89–90