Polygon
A polygon (from ancient Greek πολυγώνιον polygṓnion 'polygon'; from πολύς polýs 'much' and γωνία gōnía 'angle') or polygon is a flat geometric figure in elementary geometry that is formed by a closed line .
A polygon is a two-dimensional polytope .
A polygon is obtained by (non-collinear) in a plane at least three different points by stretching are bonded together. This creates a closed line ( polygon ) with as many corners , for example a triangle (3 points, 3 lines) or a square (4 points, 4 lines).
The enclosed area is often referred to as a polygon, as in planimetry .
Definition and terms
A polygon is a figure defined by a tuple of different points.
- The points are called the corner points or corners of the polygon for short , a polygon with corners is called -Eck or (especially in English literature) also -on.
- The lines and are called the sides of the polygon.
- All connecting lines between two corner points that are not sides are called diagonals .
Sometimes further conditions are required for the definition of a polygon, but they are not formally necessary:
- A polygon has at least three corner points that differ from one another in pairs. That excludes a "two-corner".
- Three adjacent corner points are not on a straight line. Also , , and , , will be considered as adjacent vertices. This excludes corners with straight angles.
classification
By number of corners
Polygons are typically named after the number of corners (weight of the polygon).
Regular polygon
If a polygon has the same sides and the same interior angles, then it is called a regular polygon or a regular polygon. Many regular polygons can be constructed with compasses and rulers ( constructible polygons ).
Z + L means: can be constructed with a compass and ruler.
| Corners | designation | Latin | Z + L | Specialty |
|---|---|---|---|---|
| 1 | One corner | Monogonic | - | Point |
| 2 | Delta | Digon | - | Straight |
| 3 | triangle | Trine | Yes | 1. Fermat prime number |
| 4th | square | Tetragon | Yes | square |
| 5 | pentagon | Pentagon | Yes | 2. Fermat prime number |
| 6th | hexagon | hexagon | Yes | |
| 7th | heptagon | heptagon | No | Approximate construction possible |
| 8th | octagon | Octagon | Yes | english oct a gon |
| 9 | Neuneck | Nonagon | No | rarer Enneagon , approximation construction possible |
| 10 | decagon | Decagon | Yes | |
| 11 | Elf | Hendekagon | No | Approximate construction possible |
| 12 | Dodecagon | Dodecagon | Yes | |
| 13 | Triangle | Tridecagon | No | |
| 14th | Fourteen | Tetradecagon | No | |
| 15th | Fifteenth | Pentadecagon | Yes | |
| 16 | Hexagon | Hexadecagon | Yes | |
| 17th | Seventeenth corner | Heptadecagon | Yes | 3. Fermat prime number |
| 18th | Eighteenth | Octodecagon | No | english oct a decagon, octakaidecagon |
| 19th | Nineteenth | Nonadekagon | No | English also enneadecagon , enneakaidecagon |
| 20th | Twentieth | Ikosagon | Yes | |
| 21st | Twenty One | Ikosihenagon | No | |
| 24 | Twenty-four square | Icositetragon | Yes | |
| 30th | Thirty-corner | Triakontagon | Yes | |
| 40 | Tetragonal | Tetracontagon | Yes | |
| 50 | Fifty-point | Pentacontagon | No | |
| 51 | Fifty-one | Pentacontahenagon | Yes | |
| 60 | Hexagon | Hexagon contact | Yes | |
| 70 | Seventieth | Heptakontagon | No | |
| 80 | Octagon | Octocontagon | Yes | english oct a contagon |
| 85 | Eighty-five square | Octocontapentagon | Yes | english oct a contapentagon |
| 90 | Ninety-four | Enneakontagon | No | |
| 100 | Hunderteck | Hectogon | No | |
| 257 | 257 corner | Yes | 4. Fermat's prime number | |
| 1,000 | Thousands of pieces | Chiliagon | ||
| 10,000 | Tens of thousands | Myriagon | ||
| 65,537 | 65537-corner | Yes | 5. Fermat's prime number | |
| 100,000 | Hundreds of thousands | |||
| 1,000,000 | 1000000 corner | Megagon | ||
| 4,294,967,295 | 4294967295-corner | Yes | Largest known odd number of corners that can theoretically be constructed with a compass and ruler | |
| Googoleck | Googolgon | Corner number: a 1 with 100 zeros |
More types
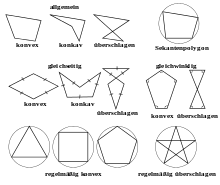
- Overturned polygon
- If the edges intersect (touch) not only at the corner points, the polygon is referred to as overturning . If there is no self-intersection, the polygon is called simple .
- Non-skipping polygon
- Polygons that are not overturned can be convex (all interior angles are smaller than 180 °) or non- convex (at least one interior angle is greater than 180 °).
- Planar polygon
- In the plane (planar) polygon.
- Non-planar polygon
- In space (non-planar) polygon.
Polygons can be equilateral or equiangular :
- Regular polygon
- If a polygon has the same sides as well as the same interior angles, then it is called a regular polygon or a regular polygon.
- Star polygon
- Planar overturned regular polygons are also known as star polygons because of their appearance .
- Orthogonal polygon
- With orthogonal polygons, all edges meet at right angles (that is, the interior angle is either 90 ° or 270 ° at each edge).
properties
angle
In a flat corner that is not overturned is the sum of the interior angles
- .
The following then applies to the sum of the outer angles regardless of the number of corners
- .
In addition, if all the inside and outside angles are the same, then these have the value
- or .
Diagonals
For polygons that are not crossed over, the following considerations apply when calculating the number of diagonals:
- Each of the corners can be connected to one of the other corners by a link.
- The connection from corner to corner is identical to the connection from to .
- Exactly connections are sides of the polygon.
So a corner that is not overturned has exactly diagonals. In the case of a non-convex polygon, there are diagonals outside the polygon (in the area of a truncated interior angle).
scope
If the corner points of a flat simple polygon are given by Cartesian coordinates , the perimeter of the polygon can be determined by adding the side lengths calculated using the Pythagorean theorem :
surface
If the corner points of a flat simple polygon are given by Cartesian coordinates , the area of the polygon can be calculated according to the Gaussian trapezoidal formula:
- .
Here, the indices that are greater than are always considered modulo , i.e. what is meant by:
In determinant form, the Gaussian trapezoidal formula is:
In addition to the Gaussian trapezoidal formula, the area of a polygon can be calculated using a signed sum of the areas of triangles that are formed with the edges of the polygon as the base and a fixed point (e.g. the point of origin) as the apex. The areas of the triangles with a base facing away from the fixed point (as the edge of the polygon) are given a negative sign.
The area of lattice polygons whose corners are all on one lattice can be calculated with Pick's theorem .
use
In computer science , important approximations of complex polygons are the convex hull and the minimally surrounding rectangle . In algorithms, a possible non-empty intersection with another geometric object is often first tested (or this is excluded) on the basis of the approximation, only then is the entire polygon loaded into memory and an exact intersection is calculated.
In 3D computer graphics , in addition to other methods of geometric modeling, any (including curved) surfaces are modeled as a polygon mesh . Triangle meshes are particularly suitable for the quick display of surfaces, but they cannot be interpolated as well using subdivision surfaces . There are a number of known data structures for storing polygonal networks.
Regular polygons are often used as a floor plan in architecture. Well-known examples:
- 16-corner: Huisduinen lighthouse near Den Helder, Netherlands
- 18-corner: Liberation Hall in Kelheim, Bavaria
- 30-Eck: Wiener Riesenrad in Vienna, Austria
See also
Web links
- Eric W. Weisstein : Polygon . In: MathWorld (English).
- For the math of irregular polygons
- Online calculation of plane polygons with graphic output
Individual evidence
- ^ Wilhelm Gemoll : Greek-German school and hand dictionary . G. Freytag Verlag / Hölder-Pichler-Tempsky, Munich / Vienna 1965.
- ↑ Cha Zhang, Tsuhan Chen: Efficient feature extraction for 2D / 3D objects in mesh representation (PDF; 66 kB). Image Processing, 2001. Proceedings. 2001 International Conference on. Vol. 3. IEEE, 2001. APA (English).