Tetragonal

Regular four-sided

A Vierzigeck or Tetrakontagon is a geometric figure , and a polygon ( polygon ). It is determined by forty points and their forty connections called lines , sides or edges.

Variations

Quadrangles can be divided into:

• overturned four-sided
• not overturned tetragonal
• concave tetragonal; at least one interior angle is greater than 180 °
• convex tetragonal; all interior angles are less than 180 °
• equilateral tetragonal; all sides are the same length
• according to the number of symmetry axes; there can be a maximum of 40
• Tendon tetragon; all corners lie on a common perimeter
• regular four-sided; all sides are the same length, all interior angles are the same size and all corner points are on a common perimeter

In the following, the regular four-sided and the regular overturned four-sided will be considered.

Regular four-sided

According to Carl Friedrich Gauß and Pierre-Laurent Wantzel, the regular four - sided is a constructible polygon , since the number of its sides can be represented as the product of a power of two with pairwise different Fermat's prime numbers ( ). ${\displaystyle 40=2^{3}\cdot 5}$

Sizes

Sizes of a regular tetragon
Interior angle	${\displaystyle {\begin{aligned}\alpha &={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {38}{40}}\cdot 180^{\circ }\\\alpha &=171^{\circ }\end{aligned}}}$
Central angle (Center angle)	${\displaystyle {\begin{aligned}\mu &={\frac {360^{\circ }}{40}}\\\mu &=9^{\circ }\end{aligned}}}$
Side length	${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{40}}\right)\\a&\approx 0{,}156918\cdot R\end{aligned}}}$
Perimeter radius	${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{40}}\right)}}\\R&\approx {\frac {a}{0{,}156918}}\end{aligned}}}$
Inscribed radius	${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {180^{\circ }}{40}}\right)\\r&\approx 0{,}996917\cdot R\end{aligned}}}$
height	${\displaystyle {\begin{aligned}h&=2\cdot r\\h&\approx 1{,}993834\cdot R\end{aligned}}}$
Area	${\displaystyle {\begin{aligned}A&=R^{2}\cdot {\frac {5}{2}}\left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)\\A&\approx 3{,}1286893\cdot R^{2}\end{aligned}}}$

Mathematical relationships

Interior angle

The interior angle is enclosed by two adjacent side edges. In the general formula for regular polygons, the variable stands for the number of corner points of the polygon. In this case, the number should be used for the variable . ${\displaystyle \alpha }$ ${\displaystyle n}$ ${\displaystyle 40}$

${\displaystyle \alpha ={\frac {n-2}{n}}\cdot 180^{\circ }={\frac {40-2}{40}}\cdot 180^{\circ }={\frac {38}{40}}\cdot 180^{\circ }=171^{\circ }}$

The sum of the interior angles is . ${\displaystyle {(n-2)\cdot 180^{\circ }}=38\cdot 180^{\circ }=6840^{\circ }}$

Central angle

The central angle or center angle is enclosed by two adjacent circumferential radii . Enter the number for the variable in the general formula . ${\displaystyle \mu }$ ${\displaystyle R}$ ${\displaystyle n}$ ${\displaystyle 40}$

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{40}}=9^{\circ }}$

Side length and perimeter radius

The quadrangle can be divided into forty isosceles triangles, so-called partial triangles . From half of such a partial triangle, i.e. from a right-angled triangle with the cathetus (half the side length) , the hypotenuse (circumferential radius) and the half central angle , the side length is obtained with the help of trigonometry in the right triangle as follows ${\displaystyle {\frac {a}{2}}}$ ${\displaystyle R}$ ${\displaystyle {\frac {\mu }{2}}}$ ${\displaystyle a}$

${\displaystyle {\begin{aligned}a&=R\cdot 2\cdot \sin \left({\frac {\mu }{2}}\right)\\&=R\cdot 2\cdot \sin \left({\frac {180^{\circ }}{40}}\right)\\a&\approx 0{,}156918\cdot R,\end{aligned}}}$

the circumferential radius is obtained by forming ${\displaystyle R}$

${\displaystyle {\begin{aligned}R&={\frac {a}{2\cdot \sin \left({\frac {180^{\circ }}{40}}\right)}}\\R&\approx {\frac {a}{0{,}156918}}\end{aligned}}}$

Inscribed radius

The incircle radius is the height of a partial triangle, perpendicular to the side of the four-sided. If the same right-angled triangle is used again for the calculation as for the side length, the inscribed radius applies ${\displaystyle r}$ ${\displaystyle a}$ ${\displaystyle r}$

${\displaystyle {\begin{aligned}r&=R\cdot \cos \left({\frac {\mu }{2}}\right)=R\cdot \cos \left({\frac {180^{\circ }}{40}}\right)\\r&\approx 0{,}996917\cdot R\end{aligned}}}$

height

The height of a regular four-sided results from the doubling of the incircle radius . ${\displaystyle h}$ ${\displaystyle r}$

${\displaystyle h=2\cdot r}$

${\displaystyle h\approx 1{,}993834\cdot R}$

Area

The area of ​​a regular n-gon is calculated from the perimeter radius according to the formula: ${\displaystyle R}$

${\displaystyle A=n\cdot {\frac {\,R^{2}}{2}}\cdot \sin \left({\frac {360^{\circ }}{n}}\right)}$.

So for the four-sided (n = 40):

${\displaystyle A=20\cdot R^{2}\cdot \sin(9^{\circ })}$.

The angle of 9 ° can be constructed with a compass and ruler and its sine has the value:

${\displaystyle \sin(9^{\circ })={\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$

Inserted results in:

${\displaystyle A=20\cdot R^{2}\cdot {\frac {1}{8}}\cdot \left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$

${\displaystyle A=R^{2}\cdot {\frac {5}{2}}\left({\sqrt {2}}\cdot \left({\sqrt {5}}+1\right)-2\cdot {\sqrt {5-{\sqrt {5}}}}\right)}$

${\displaystyle A\approx 3{,}1286893\cdot R^{2}}$

Diagonals

The quadrangle has diagonals . The diagonals have 19 different lengths. ${\displaystyle {\frac {40(40-3)}{2}}=740}$

Length L of the side and the diagonal over N sides in relation to the radius R
N L / R 1 1) 0.156918 2 0.312869 3 0.466891 4th 0.618034	N L / R 5 0.765367 6th 0.907981 7th 1.044997 8th 1.17571	N L / R 9 1.298896 10 1.414214 11 1.520812 12 1.618034	N L / R 13 1.705280 14th 1.782013 15th 1,847759 16 1.902113	N L / R 17th 1.944740 18th 1.975377 19th 1.993835 20th 2.000000

¹⁾ side of the tetragon.

construction

A regular quadrangle can only be constructed with compasses and ruler , as justified in regular quadrangle .

Construction for a given perimeter

Image 1: Regular four-sided with a given circumference

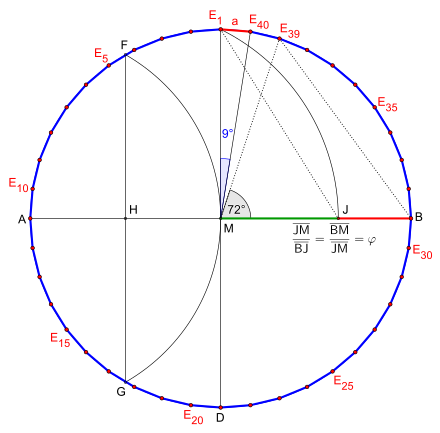
The construction in Figure 1 is similar to that of the pentagon for a given circumference . Here the segment is the side length and the angle is the central angle of the regular pentagon. ${\displaystyle {\overline {EF}}}$ ${\displaystyle GME=72^{\circ }}$

The dotted lines are not required for construction, they are only used to illustrate the following description.

It starts with the given diameter and halving it in the center. After drawing the circumference around through , the vertical central axis is drawn; Intersections are and the first corner point of the resulting four-sided. This is followed by halving the route in , resulting in the intersection points and on the perimeter. Now a is circular arc to the radius from drawn until it reaches the range in cuts. The point thus divides the distance in the ratio of the golden section . It is the result of dividing the distance in the golden ratio by the outer division . After transferring the line - the length of the side of a regular pentagon - to the circumference, the corner point is obtained. If you now halve the angle , the corner point is obtained . The connection of the corner point with creates the first side length of the four-sided. Now set the missing corner points counterclockwise on the perimeter and finally connect the neighboring corner points with each other. Thus the regular four-sided is constructed. ${\displaystyle {\overline {AB}}}$ ${\displaystyle M.}$ ${\displaystyle M}$ ${\displaystyle A}$ ${\displaystyle D}$ ${\displaystyle E_{1}}$ ${\displaystyle {\overline {AM}}}$ ${\displaystyle H}$ ${\displaystyle F}$ ${\displaystyle G}$ ${\displaystyle H}$ ${\displaystyle |HE_{1}|}$ ${\displaystyle E_{1}}$ ${\displaystyle {\overline {MB}}}$ ${\displaystyle J}$ ${\displaystyle J}$ ${\displaystyle {\overline {MB}}}$ ${\displaystyle {\overline {AJ}}}$ ${\displaystyle M}$ ${\displaystyle {\overline {E_{1}J}}}$ ${\displaystyle B}$ ${\displaystyle E_{39}.}$ ${\displaystyle E_{1}ME_{39}}$ ${\displaystyle E_{40}}$ ${\displaystyle E_{1}}$ ${\displaystyle E_{40}}$ ${\displaystyle a}$

Construction for a given side length

Image 2: Regular four-sided with a given side length

In 1822, FA Hegenberg in his work Complete Textbook of Pure Elementary Mathematics, Part Two , in the chapter Constructions of Lines and Flat Figures , Exercises and their Resolutions for Quadrangles.

Under § 776 he sets the task for a polygon with sides: ${\displaystyle n}$

“Side AB (Fig. 405. [Not visible] ) of a regular polygon of n sides is given; one should construct the polygon. "

and shows their resolution in the following second paragraph:

"If, therefore, a regular polygon is to be constructed, the side of which is given, one only needs to draw an isosceles triangle over the given side, in which the angle at the base line is equal to half the angle at the circumference of the required polygon."

The construction in Figure 2 is similar to that of the twenty-corner with a given side length .

First, the ends of the side length to the first corner points (right) and designated, then the side length is about extends beyond. This is followed by an arc with the radius around the points and ; the points of intersection and subsequently a is half-line from through pulled; it halves the length of the side in a vertical up down connects and creates the point of intersection. Then an arc is drawn around with the radius ; this results in the intersection on the extension. The route is thus divided according to the golden ratio with external division. Now an arc with the radius that intersects the half-line is drawn around . In the thus resulting isosceles triangle the angle at the corresponding angle apex of the central angle (here ) of a regular decagon, ${\displaystyle a}$ ${\displaystyle E_{1}}$ ${\displaystyle E_{40}}$ ${\displaystyle a}$ ${\displaystyle E_{1}}$ ${\displaystyle a}$ ${\displaystyle E_{1}}$ ${\displaystyle E_{40}}$ ${\displaystyle A}$ ${\displaystyle B.}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle a}$ ${\displaystyle C.}$ ${\displaystyle {\overline {E_{1}E_{40}}}}$ ${\displaystyle E_{1}}$ ${\displaystyle D.}$ ${\displaystyle C}$ ${\displaystyle |E_{40}D|}$ ${\displaystyle F}$ ${\displaystyle {\overline {E_{40}F}}}$ ${\displaystyle E_{40}}$ ${\displaystyle {\overline {E_{40}F}}}$ ${\displaystyle G}$ ${\displaystyle E_{40}E_{1}G}$ ${\displaystyle G}$ ${\displaystyle \mu '}$

because for a side length applies in a right triangle ${\displaystyle a=1}$ ${\displaystyle E_{40}CG}$

${\displaystyle {\begin{aligned}\sin \left({\frac {1}{2}}\mu '\right)&={\frac {\frac {a}{2}}{{\frac {1}{2}}+{\frac {\sqrt {5}}{2}}}}={\frac {a}{2\cdot \left({\frac {1}{2}}+{\frac {\sqrt {5}}{2}}\right)}}\end{aligned}}}$

with inserted values

${\displaystyle {\begin{aligned}\sin \left({\frac {\mu '}{2}}\right)&={\frac {0{,}5}{{\frac {1}{2}}+{\frac {\sqrt {5}}{2}}}}\\\end{aligned}}}$

from this follows for angles ${\displaystyle {\frac {\mu '}{2}}}$

${\displaystyle {\begin{aligned}{\frac {\mu '}{2}}&=\arcsin \left({\frac {0{,}5}{{\frac {1}{2}}+{\frac {\sqrt {5}}{2}}}}\right)=18^{\circ }\end{aligned}}}$

thus the angle is equal to the central angle of the decagon. ${\displaystyle \mu '=36^{\circ }}$

It continues with the arc around the point with the radius ; he cuts in the half-line, the off by runs. Because , according to the Zentriwinkelsatz the angular width at the angle vertex of the isosceles triangle half as large as the angular width at the angle vertex of the isosceles triangle A further circular arc, this time around the point of radius , has the same half-line in cut, thus producing at the angle point of the central angle of the Vierzigecks . ${\displaystyle G}$ ${\displaystyle {\overline {E_{40}G}}}$ ${\displaystyle H}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle {\overline {E_{40}G}}={\overline {GH}}}$ ${\displaystyle H}$ ${\displaystyle E_{40}E_{1}H}$ ${\displaystyle \left(18^{\circ }\right),}$ ${\displaystyle \mu '=36^{\circ }}$ ${\displaystyle G}$ ${\displaystyle E_{40}E_{1}G.}$ ${\displaystyle H}$ ${\displaystyle {\overline {E_{40}H}}}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle \mu =9^{\circ }}$

Now draw the perimeter around the center point , fix the missing corner points counterclockwise on the perimeter and finally connect the neighboring corner points with each other. Thus the regular four-sided is constructed. ${\displaystyle M}$

Regular overturned four-sided

It results when at least one is skipped each time when connecting the forty corner points and the chords thus created are of the same length. Such regular stars are noted with Schläfli symbols , indicating the number of corner points and connecting every -th point. ${\displaystyle \left\{n/k\right\}}$ ${\displaystyle n}$ ${\displaystyle k}$

There are only seven regular forty-ray stars.

The "star" with the symbols {40/2} and {40/38} are regular Twenty corner , {40/4} and {40/36} regular tens corner , {40/5} and {40/35} regular octagons , {40/8} and {40/32} regular pentagons , {40/10} and {40/30} regular quadrilaterals . The stars with the symbols {40/6} and {40/34}, {40/14} and {40/26} as well as {40/18} and {40/22} are regular twenty-ray stars, {40/12} and {40/28} are regular ten-ray stars, {40/15} and {40/25} regular eight-ray stars, and finally {40/16} and {40/24} regular pentagrams .

• Regular forty-ray stars
• 

  ${\displaystyle \left\{40/3\right\}{,}\ \left\{40/37\right\}}$

• 

  ${\displaystyle \left\{40/7\right\}{,}\ \left\{40/33\right\}}$

• 

  ${\displaystyle \left\{40/9\right\}{,}\ \left\{40/31\right\}}$

• 

  ${\displaystyle \left\{40/11\right\}{,}\ \left\{40/29\right\}}$

• 

  ${\displaystyle \left\{40/13\right\}{,}\ \left\{40/27\right\}}$

• 

  ${\displaystyle \left\{40/17\right\}{,}\ \left\{40/23\right\}}$

• 

  ${\displaystyle \left\{40/19\right\}{,}\ \left\{40/21\right\}}$

Web links

• Quadrangular Walter Payton's Roundhouse (Former)

Individual evidence

1. ^ FA Hegenberg: Complete textbook of pure elementary mathematics, second part . Theodor Christian Friedrich Enslin, 1822, online copy (Google) p. 381, § 776 , cover sheet ; accessed on April 20, 2018