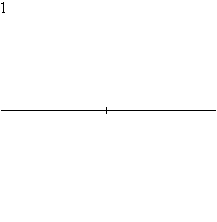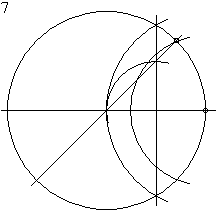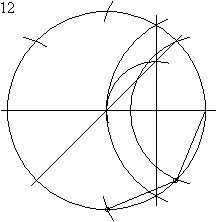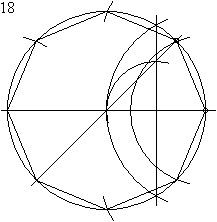octagon

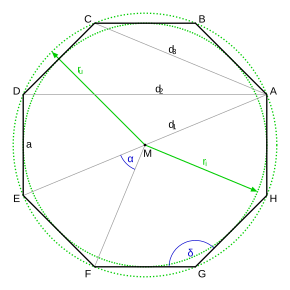
Fig. 1
Regular (convex) octagon

An octagon (also octagon or octagon, from Latin octogonum, octagonum, octagonon, from Greek ὀκτάγωνον oktágōnon ) is a geometric figure and a polygon ( polygon ) with eight corners and eight sides. Octagons, like all polygons that are not triangles , can be divided into convex, concave and overturned octagons. In variations of this will be described in detail and illustrated after that, the regular octagon in detail.

Variations

Image 3
Above: concave octagon
Below: overturned octagon

Fig. 2
Irregular octagon

The octagon can be represented as:

convex octagon in which all interior angles are less than 180 °. A convex octagon can be regular (picture 1) or irregular (picture 2).

The regular octagon is determined by eight points on a virtual or real circle. The neighboring points are to each other always at the same distance and are connected by juxtaposed tracks , even sides or edges , called connected.

concave octagon (Fig. 3), in which at least one interior angle is greater than 180 °.
Overturned octagon (picture 3): An overturned octagon can be regular or irregular.

Fig. 5
tendon octagon

Fig. 4
Regular overturned octagon
star

{\ displaystyle \ left \ {8/3 \ right \} {,} \ \ left \ {8/5 \ right \}}

The regular overturned octagon (Fig. 4) results when at least one is skipped over each time when connecting the eight corner points and the chords thus created are of the same length. Such regular stars are noted with Schläfli symbols , indicating the number of corner points and connecting every -th point . ${\ displaystyle \ left \ {n / k \ right \}}$ ${\ displaystyle n}$ ${\ displaystyle k}$

There is only one regular eight- ray star , also called an eighth star or octogram .

The "stars" with the symbols {8/2} and {8/6} are squares . If you place these two squares with their axis and diagonal lines on top of each other and then turn them by 45 ° relative to each other, see the white triangles in the star, you get an octagon .

Chord octagon (Fig. 5) in which all corners lie on a common perimeter , but the side lengths may be unequal.

Regular octagon

Formulas

Mathematical formulas for the regular octagon
Area	${\ displaystyle A = (2 + 2 \ cdot {\ sqrt {2}}) \ cdot a ^ {2} \ approx 4 {,} 828 \ cdot a ^ {2}}$
Area	${\ displaystyle A = 2 \ cdot {\ sqrt {2}} \ cdot r _ {\ mathrm {u}} ^ {2} \ approx 2 {,} 828 \ cdot r _ {\ mathrm {u}} ^ {2} }$
Length of the diagonal	${\ displaystyle d_ {1} = 2 \ cdot r _ {\ mathrm {u}} = {\ sqrt {4 + 2 {\ sqrt {2}}}} \ cdot a \ approx 2 {,} 613 \ cdot a}$
	${\ displaystyle d_ {2} = 2 \ cdot r _ {\ mathrm {i}} = (1 + {\ sqrt {2}}) \ cdot a \ approx 2 {,} 414 \ cdot a}$
	${\ displaystyle d_ {3} = {\ sqrt {2}} \ cdot r _ {\ mathrm {u}} = {\ sqrt {2 + {\ sqrt {2}}}} \ cdot a \ approx 1 {,} 848 \ cdot a}$
Inscribed radius	${\ displaystyle r _ {\ mathrm {i}} = {\ frac {1 + {\ sqrt {2}}} {2}} \ cdot a \ approx 1 {,} 207 \ cdot a}$
Perimeter radius	${\ displaystyle r _ {\ mathrm {u}} = {\ frac {1} {2}} \ cdot {\ sqrt {4 + 2 {\ sqrt {2}}}} \ cdot a \ approx 1 {,} 307 \ cdot a}$
Central angle	${\ displaystyle \ alpha = {\ frac {360 ^ {\ circ}} {8}} = 45 ^ {\ circ}}$
Interior angle	${\ displaystyle \ delta = 180 ^ {\ circ} - \ alpha = 135 ^ {\ circ}}$

Area calculation

Divide the regular octagon into 8 isosceles triangles . The angle enclosed by their legs is 360 ° / 8 = 45 °. The two base angles of the triangle are each 67.5 °. The height bisects the isosceles triangle. By drawing in the height, a right-angled triangle with the angles 67.5 °, 22.5 ° and 90 ° is created. The following approaches are based on this right-angled triangle, where:

${\ displaystyle a}$ is the side length of the octagon.
${\ displaystyle a '}$ is half the side of the octagon.
${\ displaystyle r _ {\ mathrm {i}}}$ is the radius of the inscribed circle .
${\ displaystyle r _ {\ mathrm {u}}}$ is the radius of the perimeter .
${\ displaystyle A}$ is the area of the octagon.
${\ displaystyle A '}$ is the area of the right triangle .

The radius of the inscribed circle is given: ${\ displaystyle r _ {\ mathrm {i}}}$
The leg you are looking for (opposite cathetus to the acute angle) can be determined using the tangent of 22.5 °:

{\ displaystyle a '= r _ {\ mathrm {i}} \ cdot \ tan 22 {,} 5 ^ {\ circ}}

The area of the right triangle is obtained by

{\ displaystyle A '= {\ frac {a' \ cdot r _ {\ mathrm {i}}} {2}} = {\ frac {(r _ {\ mathrm {i}} \ cdot \ tan 22 {,} 5 ^ {\ circ}) \ cdot r _ {\ mathrm {i}}} {2}} = {\ frac {r _ {\ mathrm {i}} ^ {2} \ cdot \ tan 22 {,} 5 ^ {\ circ}} {2}}}

The isosceles triangle is twice the area of the right triangle, the octagon is eight times the area of the isosceles triangle:

{\ displaystyle A = 2 \ cdot 8 \ cdot A '= 16 \ cdot \ left ({\ frac {r _ {\ mathrm {i}} ^ {2} \ cdot \ tan 22 {,} 5 ^ {\ circ} } {2}} \ right) = 8 \ cdot r _ {\ mathrm {i}} ^ {2} \ cdot \ tan 22 {,} 5 ^ {\ circ}}

The length of the sides of the octagon is given: ${\ displaystyle a}$
Analogous to the above consideration, the radius of the inscribed circle can be determined with the help of the tangent of 22.5 °, let it be half of : ${\ displaystyle r _ {\ mathrm {i}}}$ ${\ displaystyle a '}$ ${\ displaystyle a}$

{\ displaystyle r _ {\ mathrm {i}} = {\ frac {a '} {\ tan 22 {,} 5 ^ {\ circ}}}}

The area of the right triangle is obtained by

{\ displaystyle A '= {\ frac {a' \ cdot r _ {\ mathrm {i}}} {2}} = {\ frac {a '^ {2}} {2 \ cdot \ tan 22 {,} 5 ^ {\ circ}}}}

If you put in the formula for the total area, you get ${\ displaystyle A '}$

{\ displaystyle A = 8 \ cdot 2 \ cdot A '= 16 \ cdot {\ frac {a' ^ {2}} {2 \ cdot \ tan 22 {,} 5 ^ {\ circ}}} = {\ frac {8 \ cdot a '^ {2}} {\ tan 22 {,} 5 ^ {\ circ}}} = {\ frac {2 \ cdot a ^ {2}} {\ tan 22 {,} 5 ^ { \ circ}}}}

The radius of the perimeter is given: ${\ displaystyle r _ {\ mathrm {u}}}$
The ratio to corresponds to the sine of the acute angle : ${\ displaystyle a '}$ ${\ displaystyle r _ {\ mathrm {u}}}$

{\ displaystyle a '= r _ {\ mathrm {u}} \ cdot \ sin 22 {,} 5 ^ {\ circ}}

The radius of the inscribed circle is ${\ displaystyle r _ {\ mathrm {i}}}$

{\ displaystyle r _ {\ mathrm {i}} = {\ frac {a '} {\ tan 22 {,} 5 ^ {\ circ}}} = {\ frac {r _ {\ mathrm {u}} \ cdot \ sin 22 {,} 5 ^ {\ circ}} {\ tan 22 {,} 5 ^ {\ circ}}} = r _ {\ mathrm {u}} \ cdot \ cos 22 {,} 5 ^ {\ circ} }

The area of the right triangle is obtained by

{\ displaystyle A '= {\ frac {a' \ cdot r _ {\ mathrm {i}}} {2}} = {\ frac {r _ {\ mathrm {u}} ^ {2} \ cdot \ sin 22 { ,} 5 ^ {\ circ} \ cdot \ cos 22 {,} 5 ^ {\ circ}} {2}}}

If you put in the formula for the total area, you get ${\ displaystyle A '}$

{\ displaystyle A = 8 \ cdot 2 \ cdot A '= 16 \ cdot \ left ({\ frac {r _ {\ mathrm {u}} ^ {2} \ cdot \ sin 22 {,} 5 ^ {\ circ} \ cdot \ cos 22 {,} 5 ^ {\ circ}} {2}} \ right) = 8 \ cdot r _ {\ mathrm {u}} ^ {2} \ cdot \ sin 22 {,} 5 ^ {\ circ} \ cdot \ cos 22 {,} 5 ^ {\ circ}}

or with the addition theorems for the trigonometric functions

{\ displaystyle A = 4 \ cdot r _ {\ mathrm {u}} ^ {2} \ cdot \ sin 45 ^ {\ circ}}

Geometric constructions

With a given radius

Construction of a regular octagon with a given circumference

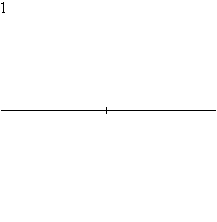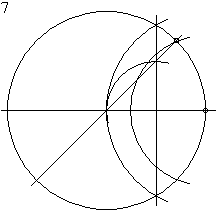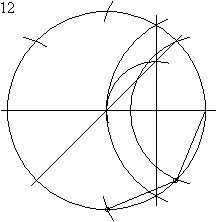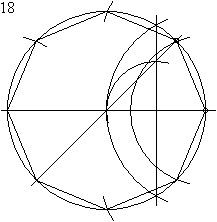
Octagon, constructed of a square, circle diameter by diagonal specified

{\ displaystyle d_ {1}}

You can construct a regular octagon by constructing the symmetry axes of a square using the perpendiculars and connecting their points of intersection with the circumference , with the corners of the square. ${\ displaystyle M _ {\ mathrm {S}}}$

The animation below shows an alternative.

For a given side length

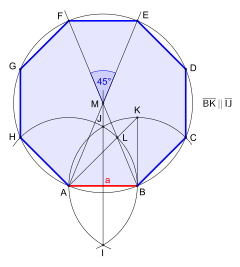
Construction of a regular octagon with a given side length, see animation.

The construction is almost the same as that of the regular hexagon with a given side length .

First, the two end points of the side length are denoted by and . Both are corner points of the resulting octagon. This is followed by an arc with the radius around the point and a second with the same radius around the point , resulting in the two intersection points and . It continues with the half-line from through and drawing a parallel to from the point that the arc around in cuts. Now the point is connected with, creating the point of intersection . Then the half-line is drawn through , cutting the half-line in . Thus the center of the resulting octagon is determined. The second half straight through leads to the central angle . After drawing in the circumference around and through , the corners and the octagon result. Now remove the two missing side lengths on the circumference, they result in the corners and , and finally connect the neighboring corners to a finished octagon. ${\ displaystyle a}$ ${\ displaystyle A}$ ${\ displaystyle B}$ ${\ displaystyle a}$ ${\ displaystyle B}$ ${\ displaystyle A}$ ${\ displaystyle I}$ ${\ displaystyle J}$ ${\ displaystyle I}$ ${\ displaystyle J}$ ${\ displaystyle {\ overline {IJ}}}$ ${\ displaystyle B}$ ${\ displaystyle B}$ ${\ displaystyle K}$ ${\ displaystyle K}$ ${\ displaystyle A}$ ${\ displaystyle L}$ ${\ displaystyle B}$ ${\ displaystyle L}$ ${\ displaystyle I}$ ${\ displaystyle M}$ ${\ displaystyle M}$ ${\ displaystyle A}$ ${\ displaystyle M}$ ${\ displaystyle 45 ^ {\ circ}}$ ${\ displaystyle M}$ ${\ displaystyle A}$ ${\ displaystyle C, E, F}$ ${\ displaystyle H}$ ${\ displaystyle a}$ ${\ displaystyle D}$ ${\ displaystyle G}$

The center angle with the angular width results from the similar triangles ${\ displaystyle \ mu}$ ${\ displaystyle 45 ^ {\ circ}}$ ${\ displaystyle \ Delta BLA \ sim \ Delta ABM:}$