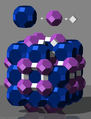
Archimedean body

The Archimedean solids are a class of regular geometric solids . They are convex polyhedra ( polyhedra ) with the following properties:
- their side faces are regular polygons (polygons),
- all corners of the body are completely identical to each other (uniformity of the corners), and
- they are neither platonic solids nor prisms or antiprisms .
Depending on the counting method, there are 13 or 15 such bodies. They are named after the Greek mathematician Archimedes , who probably discovered them all in the third century BC. Archimedes' writing has not survived , only a summary by the Alexandrian mathematician Pappos (4th century AD) has survived.
definition
The exact definition of the uniformity of the corners takes some effort and is not always uniform.
First, consider all convex polyhedra whose faces are regular polygons and which meet the global uniformity of the corners :
- The symmetry group of the polyhedron operates transitively on its vertices.
This clearly means:
- For each pair of corners of the polyhedron it is possible to rotate and mirror the polyhedron in such a way that the corner comes to lie where the corner was previously and the two positions of the polyhedron before and after the rotation cannot be distinguished.
There are several simple classes of convex polyhedra that meet all of these properties:
- The five platonic solids .
- All prisms that consist of exactly two congruent regular n corners and n squares. Such a prism exists for every natural number . An n corner and two squares always meet at one corner . In this case, the result is a cube , i.e. a platonic solid.
- All antiprisms that consist of exactly two congruent n corners and 2 n equilateral triangles. There is such an antiprism for every natural number . An n corner and three triangles always meet at one corner . In the case , there is an octahedron , i.e. a platonic solid.
The Archimedean solids are now defined as all convex polyhedra with regular side faces, which meet the global uniformity of the corners and do not fall into one of these three classes mentioned.
properties
- If one does not differentiate between similar bodies, there are exactly 13 Archimedean bodies. Of two of these bodies - the beveled hexahedron and the beveled dodecahedron - there are two mirror-inverted variants each, which cannot be converted into one another by turning. Occasionally these are counted twice, so that a total of 15 Archimedean solids result from this counting method.
- Because the side faces are regular polygons, the following applies: All edges of an Archimedean solid have the same length.
- The local uniformity of the corners follows from the global uniformity of the corners :
- The same types of polygons meet at each corner, read clockwise or counterclockwise.
- However, the global uniformity does not generally follow from the local uniformity of the corners. The pseudo-diamond cuboctahedron provides a counterexample .
- The sequence of areas at a corner clearly characterizes every Archimedean (as well as Platonic) solid.
- The polyhedra dual to the Archimedean solids are the Catalan solids . The characteristic property of these bodies is the uniformity of the surfaces , which results from the uniformity of the corners of the Archimedean bodies.
- Any Archimedean solid can be created from a Platonic solid by blunting. The name of many Archimedean bodies also suggests this. By blunting a body it is meant here that arbitrary pieces are cut away from the body, but the surfaces of the body - usually reduced in size - are retained as surfaces of the blunted body.
- If an Archimedean solid can be generated from a platonic solid by blunting, then it can also be generated from the dual platonic solid by blunting.
Derivations from the Platonic Solids
Most Archimedean solids can be clearly derived from the Platonic solids (see the detailed description under Archimedean solid - Construction of Archimedean solids ). The simplest operation is blunting, rectification, double blunting, and double rectification. These are variants of blunting of varying degrees. The truncation planes (cutting planes) are pushed concentrically towards the center of the present Platonic solid until the side surfaces of the Platonic solid or these cutting planes meet at a point or the cutting edges of these side surfaces or cutting planes have the same length as the remaining edges of the original Platonic solid. The cantellation, beveling and cantitruncation are somewhat more demanding. The following table gives an overview of the resulting bodies:
In the case of the tetrahedron , not all the resulting polyhedra are Archimedean solids. Double truncation creates the octahedron and chamfering creates the icosahedron .
The individual Archimedes' bodies
| Surname | photos | Surfaces | edge | Corners | Surface sequence at the corners |
Symmetry group |
Dual body | ||
|---|---|---|---|---|---|---|---|---|---|
| Truncated tetrahedron |

|

|
8th | 4 triangles 4 hexagons |
18th | 12 | 3, 6, 6
|
T d | Triacistrahedron |
| Cuboctahedron |

|

|
14th | 8 triangles 6 squares |
24 | 12 | 3, 4, 3, 4
|
O h | Rhombic dodecahedron |
| Truncated hexahedron |

|

|
14th | 8 triangles 6 octagons |
36 | 24 | 3, 8, 8
|
O h | Triakis octahedron |
| Truncated octahedron |

|

|
14th | 6 squares 8 hexagons |
36 | 24 | 4, 6, 6
|
O h | Tetrakis hexahedron |
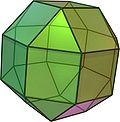
| Diamond cuboctahedron |
|

|
26th | 8 triangles 18 squares |
48 | 24 | 3, 4, 4, 4
|
O h | Deltoidal icositetrahedron |
|
Large rhombic cuboctahedron or truncated cuboctahedron |

|

|
26th | 12 squares 8 hexagons 6 octagons |
72 | 48 | 4, 6, 8
|
O h | Hexakis octahedron |
|
Beveled hexahedron or cubus simus |

|

|
38 | 32 triangles 6 squares |
60 | 24 | 3, 3, 3, 3, 4
|
O | Pentagonikositetrahedron |
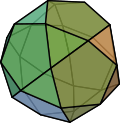
| Icosidodecahedron |
|

|
32 | 20 triangles 12 pentagons |
60 | 30th | 3, 5, 3, 5
|
I h | Rhombic triacontahedron |
| Truncated dodecahedron |
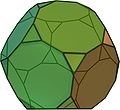
|

|
32 | 20 triangles 12 decagons |
90 | 60 | 3, 10, 10
|
I h | Triakis icosahedron |
|
Truncated icosahedron or soccer ball |

|

|
32 | 12 pentagons 20 hexagons |
90 | 60 | 5, 6, 6
|
I h | Pentakis dodecahedron |
| Rhombicosidodecahedron |

|

|
62 | 20 triangles 30 squares 12 pentagons |
120 | 60 | 3, 4, 5, 4
|
I h | Deltoid hexacontahedron |
|
Large rhombicosidodecahedron or truncated icosidodecahedron |

|

|
62 | 30 squares 20 hexagons 12 decagons |
180 | 120 | 4, 6, 10
|
I h | Hexakis icosahedron |
|
Beveled dodecahedron or dodecaedron simum |

|

|
92 | 80 triangles 12 pentagons |
150 | 60 | 3, 3, 3, 3, 5
|
I. | Pentagon hexacontahedron |
Room fillings with Archimedean bodies
The three-dimensional Euclidean space can be completely filled with Platonic solids or Archimedean solids of the same edge length. Such three-dimensional tiling is called room filling . The following fillings contain Archimedean solids:
Room filling that consists only of truncated octahedra
Room filling with truncated tetrahedron and tetrahedron
Room filling with cuboctahedron and octahedron
Room filling with truncated hexahedron and octahedron
Room filling with rhombic cuboctahedron , cube and tetrahedron
Room filling with rhombic cuboctahedron , cuboctahedron and cube
The three-dimensional Euclidean space can be parquet-free with truncated octahedra . That is the only Archimedean body with which this is possible.
The pseudo-rhombic cuboctahedron
For a long time, the definition of the Archimedean solids was not based on the global, but rather the more descriptive local uniformity of the corners. It was not until 1930 that the British mathematician JCP Miller discovered that there was a convex polyhedron with regular faces, which fulfilled the local uniformity of the corners, but had not yet been recognized as an Archimedean solid. This polyhedron is created when you twist a cap of the rhombic cuboctahedron by 45 degrees. It is known as the pseudo-rhombic cuboctahedron , Miller's solid, or Johnson's body .
In every corner of this body, as in the case of a rhombic cuboctahedron, three squares and a triangle collide, so the local uniformity of the corners is given. In contrast to the classical Archimedean solids, two different types of corners can be distinguished. To do this, however, it is necessary not only to consider the areas directly adjacent to the corner, but also to include the areas which are further away from the corner in order to distinguish them.
Occasionally, the pseudo-rhombic cuboctahedron is classified as the 14th Archimedean solid. Usually, however, the prevailing opinion is that it should not be viewed as an Archimedean solid due to the different types of corners. The requirement of the strong uniformity of the corners then ensures that the pseudo-rhombic cuboctahedron is excluded from the definition.
One can speculate that possibly already Kepler knew the pseudo-rhombic cuboctahedron: for once he speaks of fourteen Archimedean solids.
See also
literature
- Paul Adam, Arnold Wyss: Platonic and Archimedean solids, their star shapes and polar structures. Verlag Free Spiritual Life u. a., Stuttgart 1984, ISBN 3-7725-0965-7 (2nd edition. Haupt et al., Bern 1994).
Individual evidence
- ^ Pappus of Alexandria : Mathematicae collectiones . tape V , no. 19 .
- ^ Branko Grünbaum : An enduring error . In: Elements of Mathematics . 64, No. 3, 2009, pp. 89-101. doi : 10.4171 / EM / 120 . Reprinted in Mircea Pitici (Ed.): The Best Writing on Mathematics 2010 . Princeton University Press, 2011, ISBN 978-0-691-14841-0 , pp. 18-31 .
- ^ Peter R. Cromwell: Polyhedra . Cambridge University Press , 1997, ISBN 0-521-55432-2 , p. 156 ( limited preview in Google Book Search [accessed December 28, 2016]).