Room filling

from Wikipedia, the free encyclopedia

Room filling or tiling of three-dimensional space refers to the filling of (usually) 3-dimensional Euclidean spaces with structures that have at most the same dimensions as this space. For the two-dimensional case of tiling, see tiling . Space fills can trivially be complete, i.e. H. the entire volume is occupied (as with a completely filled glass), or partially, which leads to the interesting problem of spatially closest packing of spheres . In many practical applications there is an interest in optimizing the density of the filling, for example in thePackaging industry . Room fillings mathematically abstracted can be found u. a. for the space-filling curves , where fractal structures with a fractional dimension smaller than the space dimension n and larger than n − 1 are used for filling. Natural quasi-fractals of this type are often found as supply networks in biological organisms ( blood vessel system , tracheal system ).

Space filling with polyhedra

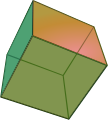
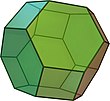
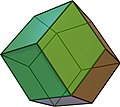
A gapless space filling with polyhedra is also called tiling of the three-dimensional space . If one tries to fill the space with polyhedra of one kind, there are exactly five of the convex polyhedra bounded by regular polygons that fill the space alone: cube , triangular and hexagonal prism , truncated octahedron and the twisted double wedge ( Johnson body J 26 , also Gyrobifastigium ). The latter four contain two types of polygons with different numbers of corners. Among the so-called Catalan solids , only the rhombic dodecahedron is space-filling.

  • cube

  • hexagonal prism

  • triangular prism

  • twisted double wedge

  • Truncated octahedron

  • Rhombic dodecahedron

In 1885, Evgraf Stepanowitsch Fjodorow classified the space-filling parallelohedra, i.e. polyhedra that can be converted into one another by translation ( affine types of convex parallelohedra ) and found five in three-dimensional space: parallelepiped , hexagonal prism , rhombic dodecahedron , elongated rhombic dodecahedron and truncated octahedron . This became important for his classification of crystallographic space groups.

Crystallographic restriction

An interesting phenomenon occurs with periodic tiling: their symmetry groups can only contain rotations of 360 °, 180 °, 120 °, 90 ° and / or 60 ° (i.e. elements of orders 1, 2, 3, 4 and 6), but none Rotations by other angles (ie no elements of orders 5, 7 or higher). This fact, which, by the way, also applies to “real” crystals , is called “crystallographic restriction”. However, order 5 is possible with quasicrystals that have an “almost” periodic division.

Types of 3D tiling

Parquet flooring of the room using truncated hexahedra and octahedra

The following are examples of how the three-dimensional space can be completely filled with regular or semi-regular polyhedra of the same edge length. The number of polyhedra that is required to form a full solid angle of 4π is given.

See also

Individual evidence

  1. ↑ Eberhard Scholz, Symmetrie, Gruppe, Dualität, Birkhäuser 1989, p. 117