Tetrahedron
| Regular tetrahedron, a platonic solid | |
|---|---|

|
|
| Type of side surfaces | equilateral triangles |
| Number of faces | 4th |
| Number of corners | 4th |
| Number of edges | 6th |
| Schläfli icon | {3.3} |
| dual to | Tetrahedron |
|
Body network in the picture one of two possible networks |

|
| Number of different networks | 2 |
| Number of edges in a corner | 3 |
| Number of corners of a surface | 3 |
The (also, especially southern Germany , of ) tetrahedron [ tetraeːdər ] (from ancient Greek τετρα- tetra- "four" and ἕδρα HEDRA or transferred "seat", "chair", "back", "side face"), even tetrahedron or four flat , is a body with four triangular faces . It is the only convex polyhedron ( polyhedron , polyhedron ) with four faces .
However, the word is rarely used in this general sense. Usually the tetrahedron is the regular tetrahedron with equilateral triangles as side surfaces , which is a Platonic solid.
The general tetrahedron is called a three-sided pyramid , triangular pyramid , disphenoid or three-dimensional simplex depending on its symmetry .
Regular tetrahedron
The regular tetrahedron ( regular tetrahedron ) is one of the five platonic solids , more precisely a polyhedron with
- 4 congruent equilateral triangles as side surfaces
- 6 edges of equal length and
- 4 corners where three side surfaces meet
The regular tetrahedron is also an equilateral three-sided pyramid with an equilateral triangle as its base .
symmetry
3 twofold symmetry axes
4 threefold symmetry axes
One of 6 levels of symmetry
One of 3 four-fold rotating mirror axes with rotating mirror plane
Because of its high symmetry - all corners , edges and surfaces are similar to one another - the regular tetrahedron is a regular polyhedron . It has
- 4 threefold axes of rotation (through the corners and the centers of the opposite side surfaces ),
- 3 fourfold rotating mirror axes and thus also three twofold rotation axes or three symmetry axes (through the centers of opposite edges) as well
- 6 planes of symmetry (each through an edge and perpendicular to the opposite edge).
In total, the symmetry group of the tetrahedron - the tetrahedron group - has 24 elements. It is the symmetrical group S 4 (the point group T d according to Schoenflies or 4 3m according to Hermann-Mauguin ) and causes all 4! = 24 permutations of the corners or the side surfaces . It is a subgroup of the octahedron group or cube group.
In detail belong to the tetrahedral group
- 12 rotations ( even permutations ), viz
- the identical figure ,
- 8 rotations by 120 ° (4 possible axes of rotation through each corner and the center point of the opposite triangular surface, 2 possibilities for the direction of rotation) and
- 3 rotations by 180 ° (axes of rotation through the centers of two opposite edges)
such as
- 12 odd permutations . This is obtained by performing the reflection on a fixed plane of symmetry after each of the 12 even permutations . 6 of these can also be described as a pure plane mirroring , the other six as rotational mirroring of a rotation by 90 ° around an axis that runs through the center points of two opposite edges, and a mirroring on the plane perpendicular to this axis , which is the center point between the two opposite edges.
The even permutations form a subgroup of the tetrahedral group , the so-called alternating group (the point group T or 23). Sometimes the term tetrahedron group is only used for these, excluding reflections .
The tetrahedron is the only Platonic solid that is not point-symmetric and in which every corner is opposite a surface .
Other properties
Relationship to octahedron, cube, Archimedean solids

By connecting the center points of the area you get a tetrahedron again (see figure). One therefore says: the tetrahedron is dual to itself , in short: self-dual . The side length of the inscribed tetrahedron is one third of the original side length.
With the help of these two tetrahedra bodies can be constructed that also have the tetrahedron group as a symmetry group . So you get for example
- the truncated tetrahedron with 4 hexagons and 4 triangles (see Archimedean solid ),
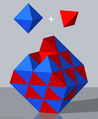
- the octahedron with 4 + 4 = 8 triangles and 6 corners (with higher symmetry ) as the intersection of two tetrahedra,
- the star tetrahedron (an octahedron with 8 attached tetrahedra) as a three-dimensional union of two tetrahedra
- the cube with 4 + 4 = 8 corners (and with higher symmetry) as the convex hull of this star body .
See also the example below.
Surrounding cube

The tetrahedron can be inscribed in a cube ( hexahedron ) in such a way that its corners are at the same time cube corners and its edges are diagonals of the cube surfaces (see illustration). The volume of this cube is three times the tetrahedral volume . The 8 corners of the cube form two disjoint sets of four corners each, which correspond to the two possible positions of the tetrahedron.
Dual to this, the tetrahedron of a cube can be described in such a way that four of the cube faces lie in the side faces of the tetrahedron and the six corners of the cube are the centers of the six tetrahedron edges . The 8 faces of the cube form two disjoint sets , which correspond to the two positions for the tetrahedron circumscribed by the cube.
angle
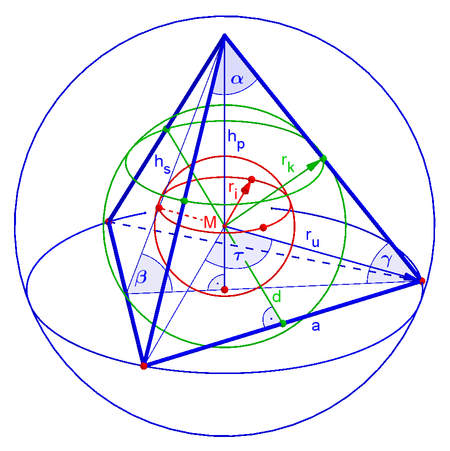
The dihedral angle between two side faces of the regular tetrahedron is 70.53 ° ( ).
Each edge forms an angle of 54.74 ° ( ) with the surface on which it stands .
The connecting lines between the center of the tetrahedron and two corners each enclose an angle of = 109.47 ° ( ).
This is known as the tetrahedral angle and it plays an important role in chemistry , for example in the geometry of the methane molecule.
The sizes of the specified angles can be determined by using trigonometric functions (see obtuse angle ). To do this, consider the sectional figure of the tetrahedron (see illustration) with one of its six planes of symmetry .
cross-section

The regular tetrahedron can be cut in two so that the cut surface is a square . The resulting parts of the tetrahedron are congruent to each other.
If the cutting plane through a regular tetrahedron is parallel to one of the four side surfaces , then the cross-section results in an equilateral triangle .
If the cutting plane through a regular tetrahedron is parallel to two opposite edges, then the cross-section results in a rectangle . If the cutting plane also has the same distance from these two edges, i.e. if it divides the remaining four edges exactly in half, then the cutting plan is a square. The square has an edge length that is exactly half the length of one edge of the tetrahedron.
example
Embedding the tetrahedron in a cube provides an easy way to construct a regular tetrahedron. If we denote the vertices of the cube at the base and as well as the overlying points with , and so form and and and respectively, the corners of a tetrahedron. If one considers z. If, for example, in a three-dimensional Cartesian coordinate system, the cube whose corners have the coordinates and , the corners are obtained for the first tetrahedron
- and .
The edges are: and . The side faces are the triangles and .
The second tetrahedron has the corners
- and .
The three-dimensional intersection of these two tetrahedra is that of the points and certain octahedra . Their union is the star tetrahedron . Its convex hull is therefore the cube .
Formulas
| Sizes of a regular tetrahedron with edge length a | ||
|---|---|---|
| volume |
|
|
| Surface area | ||
| Umkugelradius | ||
| Edge ball radius | ||
| Inc sphere radius | ||
| Pyramid height | ||
| Edge distance | ||
|
Ratio of volume to spherical volume |
||
|
Interior angle of the equilateral triangle |
||
|
Angle between adjacent faces |
||
|
Angle between edge and face |
||
| Tetrahedral angle | ||
| Solid angles in the corners | ||
Calculation of the regular tetrahedron
volume
For pyramids and thus for the tetrahedron applies
therein is the base area (equilateral triangle)
and the height of the pyramid
with inserted variables
Surface area
For the surface area of the tetrahedron (four equilateral triangles) applies
Pyramid height
The height of the pyramid can be determined using the following right-angled triangle.
The side lengths of this triangle are (see picture in formulas ): side height as a hypotenuse, pyramid height as a large cathetus and a third of the side height as a small cathetus. This value is determined by the position of the foot point of (center of gravity of the base area). The geometric center of gravity divides the height of the triangle in a ratio of 2: 1.
The following applies to the height of the equilateral triangle
and according to the Pythagorean theorem
Angle between adjacent faces
This angle, marked with , has its apex at one edge of the tetrahedron. It can be determined using the following right triangle.
The side lengths of this triangle are (see picture in formulas ): side height as a hypotenuse, pyramid height as a large cathetus and part of the side height (see heights ) as a small cathetus.
According to the Pythagorean theorem,
Angle between edge and face
This angle, marked with , has its apex at one corner of the tetrahedron. Angle can be determined using the following right triangle.
The side lengths of this triangle are (see picture in formulas ): pyramid edge as hypotenuse, pyramid height as large cathetus and part of the side height (see heights ) as small cathetus.
The following applies to the angle
Tetrahedral angle
This angle, marked with , has its apex at the center of the tetrahedron. The angle can be determined using the following right triangle.
The side lengths of this triangle are (see picture in formulas ): Umkugelradius as a hypotenuse, half the edge length as a large cathetus and half the edge distance as a small cathetus .
The following applies to the angle
Solid angles in the corners
The following formula, described in Platonic Solids, shows a solution for the solid angle
With the number of edges / faces at a corner and the interior angle of the equilateral triangle, the following applies
because of it
used in and formed
simplification
Nets of the regular tetrahedron

The tetrahedron has two nets (see figures). That means there are two different ways to unfold a hollow tetrahedron by cutting open 3 edges and spreading it out in the plane . The other 3 edges connect the 4 equilateral triangles of the network. To color a tetrahedron so that no neighboring faces are the same color, you need 4 colors.
Graphs, dual graphs, cycles, colors
The tetrahedron has an undirected planar graph with 4 nodes , 6 edges and 4 regions assigned to it. This is the complete graph K 4 . It is 3- regular , that is, 3 edges proceed from each node, so that the degree is 3 for all nodes. In the case of planar graphs, the exact geometric arrangement of the nodes is not important. However, it is important that the edges do not have to intersect. The nodes of this tetrahedron graph correspond to the corners of the tetrahedron.
The nodes of the tetrahedral graph can be colored with 4 colors in such a way that neighboring nodes are always colored differently, because all nodes are neighboring. This means that the chromatic number of this graph is 4 (see node coloring ). In addition, the edges can be colored with 3 colors so that adjacent edges are always colored differently (see illustrations). This is not possible with 2 colors, so that the chromatic index for the edge coloring is 3 (the picture on the right illustrates this coloring).
The tetrahedral graph is self-dual .
To determine the number of colors required for the areas or areas, the dual graph is helpful, which in this case is itself a tetrahedral graph with 4 nodes , 6 edges and 4 areas. The nodes of this graph are assigned one-to-one (bijective) to the areas of the original tetrahedral graph and vice versa (see bijective function and figure above). As already mentioned, the nodes of the dual tetrahedron graph can obviously only be colored with 4 colors so that neighboring nodes are always colored differently. From this it can be concluded indirectly: Because the chromatic number is 4, 4 colors are necessary for such a surface coloring of the tetrahedron or a coloring of the areas of the tetrahedron.


The 3 cut edges of each network (see above) together with the corners ( nodes ) form a spanning tree of the tetrahedron graph . Each net corresponds exactly to a spanning tree and vice versa, so that there is a one-to-one ( bijective ) assignment between nets and spanning trees. If you consider a tetrahedron network without the outer area as a graph , you get a dual graph with a tree with 4 nodes and 3 edges and the maximum node degree 3. Each area of the tetrahedron is assigned to a node of the tree. The 2 graph-theoretic constellations (see isomorphism of graphs ) each occur once.
The tetrahedral graph has 6 Hamilton circles , but no Euler circles .
Room fillings with regular tetrahedra
The three-dimensional Euclidean space can be completely filled with Platonic solids or Archimedean solids of the same edge length. Such three-dimensional tiling is called room filling . The following space fills contain tetrahedra:
Room filling with octahedron and tetrahedron
Room filling with truncated tetrahedron and tetrahedron
Room filling with rhombic cuboctahedron , cube and tetrahedron
Applications
Although the tetrahedron is not a stone of a parquet flooring of the room, it occurs in the cubic crystal system (see above).
In chemistry , the tetrahedron plays a major role in the spatial arrangement of atoms in compounds . Simple molecular shapes can be predicted with the VSEPR model . The four hydrogen atoms in the methane molecule are arranged tetrahedrally around the carbon atom , as this is how the bond angle is greatest. The carbon atoms in the diamond lattice are also arranged in a tetrahedral manner, each atom is surrounded by four other atoms. The carbon atom is then after the orbital model in sp 3 - hybridization .
The tetrahedron also gave the Tetra Pak its name because of its original shape.
Alexander Graham Bell experimented with multicellular box kites (kites), the individual cells of which have the shape of a tetrahedron. These mostly imposing dragons are called "Bell Tetrahedron". Usually 4 or 10 or 20 individual cells are put together to form a composite, which then also has the shape of a tetrahedron. However, other composite forms are also possible.
In many pen & paper role-playing games , tetrahedra are used as four-sided game dice (D4).
Further technical applications are based on the structure that results from the lines pointing from the tetrahedron center into the four corners of the room:
- Tetrapods used as breakwaters on coasts
- so-called crow's feet , a defensive weapon that is used by the police and military against cars in order to burst their tires.
Concrete tetrapod on Heligoland
Unit cell of the diamond lattice
A crow's foot of the Office of Strategic Services
Space framework made of tetrahedra
General tetrahedron
A tetrahedron in the general sense, i.e. a body with four sides , is always a three-sided pyramid , i.e. with a triangle as base and three triangles as sides, and therefore also has four corners and six edges. Since it has the smallest possible number of corners and sides for a body in space, it is called three-dimensional simplex or 3- simplex in technical terms . The two-dimensional simplices are the triangles.
- Every 3-simplex has an umkugel and an incugel .
- The center of gravity is the intersection of the connecting lines between the corners and the centers of gravity of the opposite triangles and divides them in the ratio 3: 1 ( Commandino's theorem ).
- Every 3-simplex is the convex hull of its four corners.
- It is the only known polyhedron besides the Szilassi polyhedron in which all sides are adjacent to each other.
In a tetrahedron can also by a point and the three vectors are described to adjacent points. If you denote these vectors with , then the volume of the tetrahedron is calculated with , i.e. the amount of the spat product .
The sum of the normal unit vectors pointing uniformly outwards or inwards , which are multiplied by the content of the surface on which they stand, is the zero vector , because
Calculation of any tetrahedron
A tetrahedron has 6 edges. A triangle is defined by specifying three side lengths. Each additional edge can be freely selected within certain limits. If there are 6 independent pieces of information on the size of edges or angles , you can use them to calculate the remaining edges or angles that are missing.
volume
The volume formula of the general tetrahedron was given by Leonhard Euler . With this formula the volume of the general tetrahedron can be calculated with the help of the 6 edge lengths of the tetrahedron. So the volume formula of the general tetrahedron is the same task for tetrahedral basis as for triangles of the formula of Heron .
If the edge lengths of the triangular base of the tetrahedron and the lengths of the opposite edges in space , then applies to the volume of the tetrahedron:
With
The following equations based on determinants of symmetric matrices can also be used to calculate the volume :
The first determinant is called the Cayley – Menger determinant and is used to calculate the area of any triangle (see Heron's theorem ), the volume of any tetrahedron and generally the volume of any simplex in -dimensional space .
Surface area
The area of a triangle with given side lengths can be calculated individually. The sum of the areas of the 4 triangles gives the area of the tetrahedron. For the area of the triangular base with the side lengths, for example, according to Heron's theorem :
Heights
Because every tetrahedron is a pyramid , the following equation applies to the volume , the area of the base and the corresponding height :
The volume and area can be calculated using the formulas above and then used to determine the height . The other three heights can be calculated accordingly using the area of the triangle orthogonal to the height .
Interior angles of the triangles
The interior angles of the triangles are determined using the law of cosines . For example, the inside angle of the base opposite the side applies
Angle between adjacent faces
The dihedral angle at the edge is
Here is the volume of the tetrahedron and and the area of the triangles adjacent to the edge .
Solid angles in the corners
The interior angles of the three neighboring triangles are used to calculate the solid angles in the corners of the tetrahedron :
With
generalization
The analogues of the tetrahedron in any dimension are called ( -dimensional) simplices . The -dimensional simplex has corners and is bounded by simplices of the dimension (as facets ). A zero-dimensional simplex is a point , a one-dimensional simplex is a segment , and a two-dimensional simplex is a triangle . The four-dimensional equivalent of the tetrahedron, the pentachoron , has 5 corners , 10 edges, 10 triangles as faces and 5 three-dimensional tetrahedra as facets.
The coordinates of a regular - simplex can be defined as a set in -dimensional Euclidean space :
For example , there is an equilateral triangle that is spanned by the points in three-dimensional space .
See also
literature
- Heinz Schumann: Elementary tetrahedral geometry . Franzbecker, Hildesheim 2011, ISBN 978-3-88120-521-4
Web links
Individual evidence
- ↑ Kurt Peter Müller: Spatial Geometry: Spatial Phenomena - Construct - Calculate . 2nd, revised and expanded edition. Vieweg + Teubner, 2004, ISBN 978-3-519-12397-2 , p. 81.
- ↑ Eric Weisstein, Frank Jackson: Regular Tetrahedron. Umkugelradius, formula (5). In: MathWorld Wolfram. A Wolfram Web Resource, accessed June 19, 2020 .
- ↑ Eric Weisstein, Frank Jackson: Regular Tetrahedron. Edge ball radius, formula (10). In: MathWorld Wolfram. A Wolfram Web Resource, accessed June 19, 2020 .
- ↑ Eric Weisstein, Frank Jackson: Regular Tetrahedron. In spherical radius, formula (4). In: MathWorld Wolfram. A Wolfram Web Resource, accessed June 19, 2020 .
- ↑ Harish Chandra Rajpoot: Solid angles subtended by the platonic solids (regular polyhedra) at their vertices. SlideShare, March 2015, accessed June 16, 2020 .
- ↑ Alternative expression for . WolramAlpha, accessed June 16, 2020 .
- ↑ Eric Weisstein, Frank Jackson: Regular Tetrahedron. 2 networks, above formula (1). In: Wolfram MathWorld. Wolfram Research, Inc., accessed June 19, 2020 .
- ^ Wolfram MathWorld: Tetrahedral Graph
- ^ Maximilian Miller: Stereometry. 1957, p. 41
- ↑ The title of the treatise E 231 reads roughly as follows in German: Presentation of some characteristic properties with which bodies enclosed by flat surfaces are equipped . In this treatise Euler gives the first proof of the polyhedron formula , which he already gave in an earlier treatise ( E 230 , printed under Elementa doctrinae solidorum , Novi commentarii academiae scientiarum Petropolitanae 4, pp. 109-140; cf. Introduction to the Commentationes geometricae ) mentioned but not yet proven.
- ^ Andreas Speiser et al .: Leonhardi Euleri Opera omnia. Series great. Opera mathematica. Volume XXVI: Commentationes geometricae. Volume I. 1953, pp. 106-107
- ^ IN Bronstein, KA Semendjajev et al .: Taschenbuch der Mathematik. 2008, p. 157
- ^ György Hajós: Introduction to Geometry. 1970, p. 383
- ↑ Alexander Ostermann, Gerhard Wanner: Geometry by Its History. 2012, p. 297


























































































![{\ displaystyle \ textstyle V = {\ frac {1} {6}} \ cdot \ left | \ det \ left [{\ begin {smallmatrix} {\ vec {a}} \\ {\ vec {b}} \ \ {\ vec {c}} \ end {smallmatrix}} \ right] \ right | = {\ frac {1} {6}} \ cdot \ left | ({\ vec {a}} \ times {\ vec { b}}) \ cdot {\ vec {c}} \ right |}](https://wikimedia.org/api/rest_v1/media/math/render/svg/088883ba65c5b9fa0f36e22a271178c1f3f4aff3)





























