Dodecahedron

Regular pentagon dodecahedron
Type of side surfaces	regular pentagons
Number of faces	12
Number of corners	20th
Number of edges	30th
Schläfli icon	{5.3}
dual to	Icosahedron
Body net
Number of different networks	43380
Number of edges in a corner	3
Number of corners of a surface	5

The dodecahedron [ ˌdodekaʔeːdɐ ] (from Greek. Dodecahedron ; dt. And (the) Twelve flat ) is a body with twelve faces. Usually a platonic solid is meant, namely the regular pentagonal dodecahedron , a solid with

• 12 congruent regular pentagons
• 30 edges of equal length, each of which is the side of two pentagons
• 20 corners, in each of which three of these pentagons meet

But there are also other dodecahedra of high symmetry .

The regular pentagon dodecahedron

Dodecahedron with examples of the axes of rotation and a plane of symmetry (blue) ${\displaystyle C_{5},C_{3},C_{2}}$

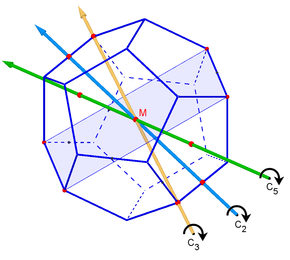
Because of its high symmetry - all corners , edges and surfaces are similar to one another - the dodecahedron is a regular polyhedron . It has:

• 6 fivefold axes of rotation (through the centers of two opposing surfaces ) ${\displaystyle C_{5}}$
• 10 threefold axes of rotation (through opposite corners) ${\displaystyle C_{3}}$
• 15 twofold axes of rotation (through the centers of opposing edges) ${\displaystyle C_{2}}$
• 15 planes of symmetry (due to opposite and parallel edges)

and is

• point symmetric (point reflection with respect to the center of the dodecahedron)

In total, the symmetry group of the dodecahedron - the dodecahedron group or icosahedron group  - has 120 elements. The 60 orientation-maintaining symmetries correspond to the alternating group . Sometimes this subgroup is also called the icosahedral group . The full symmetry group is isomorphic to the direct product . You can see that the product is direct because the point reflection at the center point commutes with the rotations . ${\displaystyle A_{5}}$ ${\displaystyle A_{5}\times C_{2}}$

The symmetry of the dodecahedron is not compatible with a periodic spatial structure due to the fivefold axes of symmetry that occur here (see tiling ). There can therefore be no crystal lattice with icosahedral symmetry (see quasicrystals ).

structure

Dodecahedron (red) with dual icosahedron (green). The centers of the regular pentagons are the corners of the icosahedron.

The icosahedron is the dual polyhedron to the dodecahedron and vice versa.

With the help of the dodecahedron and icosahedron numerous bodies can be constructed, which also have the dodecahedron group as a symmetry group . So you get for example

• the truncated dodecahedron with 12 decagons and 20 triangles by truncating the corners of a dodecahedron
• the icosidodecahedron with 12 pentagons and 20 triangles
• the truncated icosahedron (soccer ball) with 12 pentagons and 20 hexagons as the intersection of a dodecahedron with an icosahedron (see Archimedean solids , fullerenes )
• and the rhombic triacontahedron with 12 + 20 = 32 corners and 30 lozenges as faces . It is created by placing straight pyramids on the dodecahedron, of which two side faces complement each other, i.e. H. lie in one plane and have an edge in common.

From the edges of the dodecahedron, 3 pairs of opposite edges can be selected in such a way that these pairs span 3 congruent rectangles that are orthogonal to each other in pairs . The remaining 8 corners then form the corners of a cube inscribed in the dodecahedron. There are a total of five such positions, with each edge of the dodecahedron belonging to exactly one such position and each corner being the corner point of two inscribed cubes . The symmetry group of the dodecahedron causes all 5! = 120 permutations of these five positions or cubes.

Since the edges of the inscribed cube are diagonals of the pentagons, the ratio of the lengths of the edges of the dodecahedron and that of an inscribed cube corresponds to the golden ratio .

Formulas

Sizes of a dodecahedron with edge length a
volume	${\displaystyle V={\frac {a^{3}}{4}}\cdot \left(15+7\cdot {\sqrt {5}}\right)\approx 7{,}663\cdot a^{3}}$	without solid angles in the corners ${\displaystyle \Omega }$
Surface area	${\displaystyle A_{O}=3\cdot a^{2}\cdot {\sqrt {5\cdot \left(5+2\cdot {\sqrt {5}}\right)}}\;\approx 20{,}646\cdot a^{2}}$
Umkugelradius	${\displaystyle r_{u}={\frac {a}{4}}\cdot {\sqrt {3}}\cdot \left(1+{\sqrt {5}}\right)\approx 1{,}401\cdot a}$
Edge ball radius	${\displaystyle r_{k}={\frac {a}{4}}\cdot \left(3+{\sqrt {5}}\right)\approx 1{,}309\cdot a}$
Inc sphere radius	${\displaystyle r_{i}={\frac {a}{20}}\cdot {\sqrt {250+110{\sqrt {5}}}}\approx 1{,}114\cdot a}$
Ratio of volume  to spherical volume	${\displaystyle {\frac {V}{V_{UK}}}={\frac {\sqrt {15}}{6\cdot \pi }}\cdot \left(1+{\sqrt {5}}\right)\approx 0{,}665}$
Interior angle of the regular pentagon	${\displaystyle \alpha =108^{\circ }}$
Angle between adjacent faces	${\displaystyle \beta =\arccos \left(-{\frac {\sqrt {5}}{5}}\right)\approx 116^{\circ }\;33^{\prime }\;54^{\prime \prime }}$
Angle between edge and face	${\displaystyle \gamma =\arccos \left(-{\sqrt {{\frac {1}{10}}\cdot \left(5-{\sqrt {5}}\right)}}\right)}$  ${\displaystyle \approx 121^{\circ }\;43^{\prime }\;3^{\prime \prime }}$
Solid angles in the corners	${\displaystyle \Omega =\arccos \left(-{\frac {11}{25}}\cdot {\sqrt {5}}\right)\approx 2{,}962\;\mathrm {sr} }$

Calculation of the regular dodecahedron

volume

The dodecahedron consists of twelve assembled five-sided pyramids.

For a pyramid and thus for one twelfth of the dodecahedron applies

${\displaystyle V_{p}={\frac {1}{3}}\cdot A_{Gp}\cdot h_{p},}$

inside is the base ( regular pentagon )

${\displaystyle A_{Gp}={\frac {a^{2}}{4}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}}$

and the height of the pyramid is equal to the radius of the sphere ${\displaystyle h_{p}}$ ${\displaystyle r_{i}}$

${\displaystyle h_{p}={\frac {a}{20}}\cdot {\sqrt {250+110{\sqrt {5}}}},}$

from this follows with inserted variables for the volume of the dodecahedron

${\displaystyle {\begin{aligned}V&=12\cdot \left({\frac {1}{3}}\cdot {\frac {a^{2}}{4}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}\cdot {\frac {a}{20}}\cdot {\sqrt {250+110{\sqrt {5}}}}\right)={\frac {12}{3}}\cdot {\frac {1}{4}}\cdot {\frac {1}{20}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}\cdot {\sqrt {250+110{\sqrt {5}}}}\cdot a^{3}\\&={\frac {1}{20}}\cdot {\sqrt {\left(25+10\cdot {\sqrt {5}}\right)\cdot \left(250+110{\sqrt {5}}\right)}}\cdot a^{3}\;\Rightarrow \\&={\frac {a^{3}}{4}}\cdot \left(15+7\cdot {\sqrt {5}}\right)\approx 7{,}663\cdot a^{3}\;\end{aligned}}}$

Surface area

For the surface area of the dodecahedron (twelve regular pentagons) applies ${\displaystyle A_{O}}$

${\displaystyle {\begin{aligned}A_{O}&=12\cdot {\frac {a^{2}}{4}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}\cdot a^{2}\;\\&=3\cdot a^{2}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}=3\cdot a^{2}\cdot {\sqrt {5\cdot \left(5+2\cdot {\sqrt {5}}\right)}}\;\approx 20{,}646\cdot a^{2}\;\end{aligned}}}$

Angle between adjacent faces

This angle, marked with (see picture in formulas ), has its vertex at one edge of the dodecahedron. It can be determined using the following right triangle . ${\displaystyle \beta }$ ${\displaystyle MBC}$

The side lengths of this triangle are: the same as the edge ball radius as the hypotenuse, the same as the incircle radius as the large side and the same as the incircle radius of the regular pentagon as the small side. ${\displaystyle {\overline {MB}}}$ ${\displaystyle r_{k}}$ ${\displaystyle {\overline {MC}}}$ ${\displaystyle r_{i}}$ ${\displaystyle {\overline {BC}}}$ ${\displaystyle r_{i5}={\frac {a}{10}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}}$

The following applies to the angle ${\displaystyle \beta }$

${\displaystyle {\begin{aligned}\;\cos {\frac {\beta }{2}}&={\frac {r_{i5}}{r_{k}}}={\frac {{\frac {a}{10}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}}{{\frac {a}{4}}\cdot \left(3+{\sqrt {5}}\right)}}={\frac {2\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}}{5\cdot \left(3+{\sqrt {5}}\right)}}={\sqrt {{\frac {1}{10}}\left(5-{\sqrt {5}}\right)}}\;\Rightarrow \\\cos \beta &=\cos \left(\arccos \left({\sqrt {{\frac {1}{10}}\left(5-{\sqrt {5}}\right)}}\right)\cdot 2\right)=-{\frac {1}{\sqrt {5}}}\Rightarrow \\\beta &=\arccos \left(-{\frac {1}{\sqrt {5}}}\right)\approx 116^{\circ }\;33^{\prime }\;54^{\prime \prime }\;\end{aligned}}}$

Angle between edge and face

This angle, denoted by , has its apex at one corner of the dodecahedron. ${\displaystyle \gamma }$

Is, as in the illustration (see picture in formulas ), the angle z. B. searched at the corner , then it can be determined with the help of the right triangles and . Their common hypotenuse , equal to the radius of the sphere , divides the angle into the angles that are not shown, or so applies ${\displaystyle \gamma }$ ${\displaystyle D}$ ${\displaystyle DMC}$ ${\displaystyle MDE}$ ${\displaystyle {\overline {MD}}}$ ${\displaystyle r_{u}}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma _{1}}$ ${\displaystyle \gamma _{2};}$ ${\displaystyle \gamma =\gamma _{1}+\gamma _{2}.}$

The legs of the triangle with an angle are :, equal to the radius of the spherical sphere , as a large leg and , equal to the circumferential radius of the regular pentagon , as a small leg. ${\displaystyle DMC}$ ${\displaystyle \gamma _{1}}$ ${\displaystyle {\overline {MC}}}$ ${\displaystyle r_{i}}$ ${\displaystyle {\overline {CD}}}$ ${\displaystyle r_{u5}={\frac {a}{10}}\cdot {\sqrt {50+10\cdot {\sqrt {5}}}}}$

The legs of the triangle with an angle are :, equal to the edge ball radius , as a large leg and , equal to half the side , as a small leg. ${\displaystyle MDE}$ ${\displaystyle \gamma _{2}}$ ${\displaystyle {\overline {ME}}}$ ${\displaystyle r_{k}}$ ${\displaystyle {\overline {DE}}}$ ${\displaystyle {\frac {a}{2}}}$

The following applies to angles of the triangle ${\displaystyle \gamma _{1}}$ ${\displaystyle DMC}$

${\displaystyle {\begin{aligned}{\mathsf {(1)}}\;\cos \gamma _{1}&={\frac {r_{u5}}{r_{u}}}={\frac {{\frac {a}{10}}\cdot {\sqrt {50+10\cdot {\sqrt {5}}}}}{{\frac {a}{4}}\cdot {\sqrt {3}}\cdot \left(1+{\sqrt {5}}\right)}}={\sqrt {{\frac {2}{15}}\cdot \left(5-{\sqrt {5}}\right)}},\;\end{aligned}}}$

for angles of the triangle applies ${\displaystyle \gamma _{2}}$ ${\displaystyle MDE}$

${\displaystyle {\begin{aligned}{\mathsf {(2)}}\;\cos \gamma _{2}&={\frac {\frac {a}{2}}{r_{u}}}={\frac {\frac {a}{2}}{{\frac {a}{4}}\cdot {\sqrt {3}}\cdot \left(1+{\sqrt {5}}\right)}}={\sqrt {{\frac {1}{6}}\cdot \left(3-{\sqrt {5}}\right)}},\;\end{aligned}}}$

the addition theorem for the arc function gives the angle ${\displaystyle \gamma =\gamma _{1}+\gamma _{2}}$

${\displaystyle \arccos x+\arccos y=\arccos \left(xy-{\sqrt {1-x^{2}}}\cdot {\sqrt {1-y^{2}}}\right)}$

after inserting the relevant values ​​( ) applies ${\displaystyle x=\cos \gamma _{1},\;y=\cos \gamma _{2}}$

${\displaystyle {\begin{aligned}{\mathsf {(3)}}\;\gamma &=\arccos \left(\cos \gamma _{1}\cdot \cos \gamma _{2}-{\sqrt {1-\cos ^{2}\gamma _{1}}}\cdot {\sqrt {1-\cos ^{2}\gamma _{2}}}\right)\\&=\arccos \left({\sqrt {{\frac {2}{15}}\cdot \left(5-{\sqrt {5}}\right)}}\cdot {\sqrt {{\frac {1}{6}}\cdot \left(3-{\sqrt {5}}\right)}}-{\sqrt {1-\left({\frac {2}{15}}\cdot \left(5-{\sqrt {5}}\right)\right)}}\cdot {\sqrt {1-\left({\frac {1}{6}}\cdot \left(3-{\sqrt {5}}\right)\right)}}\right)\\&=\arccos \left({\frac {2}{3}}\cdot {\sqrt {{\frac {1}{5}}\cdot \left(5-2\cdot {\sqrt {5}}\right)}}-{\frac {1}{30}}\cdot {\sqrt {\left(25+11\cdot {\sqrt {5}}\right)\cdot 10}}\right)\\&=\arccos \left(-{\sqrt {{\frac {1}{10}}\cdot \left(5-{\sqrt {5}}\right)}}\right)\;\approx 121^{\circ }\;43^{\prime }\;3^{\prime \prime }.\end{aligned}}}$

Solid angles in the corners

The following formula, described in Platonic Solids, shows a solution for the solid angle ${\displaystyle \Omega }$

${\displaystyle \Omega =2\pi -2n\cdot \arcsin \left(\cos \left({\frac {\pi }{n}}\right)\cdot {\sqrt {\tan ^{2}\left({\frac {\pi }{n}}\right)-\tan ^{2}\left({\frac {\alpha }{2}}\right)}}\right)}$

With the number of edges / faces at a corner and the interior angle of the regular pentagon applies ${\displaystyle {n=3}}$ ${\displaystyle {a=108^{\circ }}}$

${\displaystyle {\begin{aligned}{\mathsf {(1)}}\;\Omega &=2\pi -2\cdot 3\cdot \arcsin \left(\cos \left({\frac {\pi }{3}}\right)\cdot {\sqrt {\tan ^{2}\left({\frac {\pi }{3}}\right)-\tan ^{2}\left({\frac {108^{\circ }}{2}}\right)}}\right)\Rightarrow \\&=2\pi -6\cdot \arcsin {\left({\sqrt {\frac {5-{\sqrt {5}}}{10}}}\right)}\approx 2{,}961739154\;sr\\\end{aligned}}}$

because of it ${\displaystyle \cos(\arcsin x)={\sqrt {1-x^{2}}}}$

${\displaystyle {\begin{aligned}{\mathsf {(2)}}\;\cos(\arcsin x)&={\sqrt {1-\left({\frac {5-{\sqrt {5}}}{10}}\right)}}\;\Rightarrow \\\end{aligned}}}$

used in and formed ${\displaystyle {\mathsf {(2)}}}$ ${\displaystyle {\mathsf {(1)}}}$

${\displaystyle {\begin{aligned}{\mathsf {(3)}}\;\Omega &=2\pi -6\cdot \arccos \left({\sqrt {{\frac {1}{10}}\cdot \left(5+{\sqrt {5}}\right)}}\right)\approx 2{,}961739154\;\mathrm {sr} .\;\end{aligned}}}$

simplification

${\displaystyle {\begin{aligned}{\mathsf {(4)}}\;\cos \Omega &=\cos \left(2\pi -6\cdot \arccos \left({\sqrt {{\frac {1}{10}}\cdot \left(5+{\sqrt {5}}\right)}}\right)\right)=-{\frac {11}{5\cdot {\sqrt {5}}}}=-{\frac {11}{25}}\cdot {\sqrt {5}}\;\Rightarrow \\\end{aligned}}}$

${\displaystyle {\begin{aligned}{\mathsf {(5)}}\;\Omega &=\arccos \left(-{\frac {11}{25}}\cdot {\sqrt {5}}\right)\approx 2{,}9617391546\;\mathrm {sr} .\;\end{aligned}}}$

Applications

• Some geodesic domes are polyhedra that are derived from the dodecahedron by further dividing the pentagons into isosceles triangles .
• There are dodecahedron-shaped dice .
• Dodecahedra are also used as original recycling bins, for example in Paris.
• In building acoustics , dodecahedral loudspeakers are used in order to achieve the best possible omnidirectional characteristic.
• Instead of a glass ball, twelve-sided crystal panels are used to illuminate the room.
• The purpose of the Roman pentagon dodecahedron is still unclear.

• A dodecahedron can also be used as an annual calendar : each month has its own pentagon .
• Both Megaminx and Alexander's Star are variants of the Rubik's Cube in the form of a dodecahedron as a three-dimensional puzzle .
• In Waldorf schools , the cornerstone that is traditionally placed at the entrance portal of every school is a copper pentagon dodecahedron.

Others

• In the science fiction film Contact (1997), the transport sphere is embedded in a lattice shaped like a dodecahedron.
• In the computer game The Dig (1995) the alien spaceship is shaped like a dodecahedron.
• 

  A dodecahedron as a dice

• 

  Megaminx , a variant of the Rubik's Cube

• 

  A dodecahedron as a poinsettia from the exhibition "Stars - not just at Christmas time" in the Museum of European Cultures in Berlin

• 

  Roman dodecahedron in the Württemberg State Museum , Stuttgart

The cubic pentagonal dodecahedron

Outwardly, the cubic pentagonal dodecahedron can easily be confused with the regular pentagonal dodecahedron. It also has 12 faces , 20 corners and 30 edges. But the surfaces are not equilateral. Each of the 12 faces has four shorter and one longer edges. The polyhedron has a total of 24 shorter and 6 longer edges. It has cubic symmetry . In nature, pyrite (FeS ₂ ) sometimes occurs in the shape of cubic pentagonal dodecahedra. Therefore the cubic pentagon dodecahedron is also called pyrite dodecahedron or pyrite dodecahedron. In crystals , five-fold axes, like the regular pentagonal dodecahedron, are impossible because there is no gapless periodic surface filling with five-fold symmetry . A regular pentagonal dodecahedron is only conceivable for non-strictly periodic “crystals”, i.e. quasicrystals .

Cubic pentagon dodecahedron

Nets of the dodecahedron

The dodecahedron has 43,380 nets . This means that there are 43380 possibilities to unfold a hollow dodecahedron by cutting open 19 edges and spreading it out in the plane . The other 11 edges each connect the 12 regular pentagons of the mesh. In order to color a dodecahedron so that no neighboring surfaces are the same color, you need at least 4 colors.

Animation of a dodecahedron network

Graphs, dual graphs, cycles, colors

Coloring is illustrated by the
dodecahedron inscribed by the dual icosahedron

The dodecahedron has an undirected planar graph with 20 nodes , 30 edges and 12 regions assigned to it, which is 3- regular , that is, 3 edges start from each node, so that the degree is 3 for all nodes. In the case of planar graphs, the exact geometric arrangement of the nodes is not important. However, it is important that the edges do not have to intersect. The nodes of this dodecahedron graph correspond to the corners of the dodecahedron.

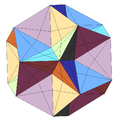
The nodes of the dodecahedron graph can be colored with 3 colors so that neighboring nodes are always colored differently. This means that the chromatic number of this graph is 3 (see node coloring ). In addition, the edges can be colored with 3 colors so that adjacent edges are always colored differently. This is not possible with 2 colors, so that the chromatic index for the edge coloring is 3 (the picture on the right illustrates this coloring).

Node coloring of the dodecahedron graph

Edge coloring of the dodecahedron graph

Area coloring of the dodecahedron graph with dual node coloring of the icosahedron graph

The dual graph (icosahedral graph ) with 12 nodes , 30 edges and 20 areas is helpful to determine the corresponding number of colors required for the surfaces or areas . The nodes of this graph are uniquely (bijectively) assigned to the areas of the dodecahedron graph and vice versa (see bijective function and figure). The nodes of the icosahedral graph can be colored with 4 colors so that neighboring nodes are always colored differently, but not with 3 colors, so that the chromatic number of the icosahedral graph is 4. From this one can indirectly conclude: Because the chromatic number is equal to 4, 4 colors are necessary for such a surface coloring of the dodecahedron or a coloring of the areas of the dodecahedron graph.

The 19 cut edges of each network (see above) together with the corners ( nodes ) form a spanning tree of the dodecahedron graph . Each net corresponds exactly to a spanning tree and vice versa, so that there is a one-to-one ( bijective ) assignment between nets and spanning trees. If you consider a dodecahedron network without the outer area as a graph, you get a dual graph with a tree with 12 nodes and 11 edges and the maximum node degree 3. Each area of ​​the dodecahedron is assigned to a node of the tree. Not every graph-theoretical constellation (see isomorphism of graphs ) of such trees occurs, but some occur several times.

The dodecahedron graph has 60 Hamilton circles , but no Euler circles .

Dodecahedron graph with one of the 60 Hamilton circles

Other dodecahedra

Other dodecahedra are for example:

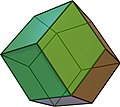
• The rhombic dodecahedron has 12 congruent rhombuses as faces , 14 corners and 24 edges. It is a Catalan solid and dual to the cuboctahedron . It forms the typical crystal shape of the garnet .
• The trigonododecahedron has 12 congruent equilateral triangles as faces, 8 corners and 18 edges. It's a deltahedron and Johnson body .
• Hollowed out dodecahedron
• Large dodecahedron
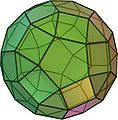
• Rhombicosidodecahedron
• Elongated rhombic dodecahedron

Some of these polyhedra have more than 12 faces, so they are not true dodecahedra.

• 

  Rhombic dodecahedron

• 

  Trigondodecahedron

• 

  Hollowed out dodecahedron

• 

  Large dodecahedron

• 

  Rhombicosidodecahedron

• 

  Elongated rhombic dodecahedron

Web links

Commons : Dodecahedron  - collection of images, videos and audio files

Wiktionary: Dodecahedron  - explanations of meanings, word origins, synonyms, translations

• Euclid: Stoicheia. Book XIII.17. Dodecahedron of a sphere ...
• Derivation of the formulas
• Craft sheet for calendars in dodecahedron shape
• Dodecahedron . Math tinkering
• Dodecahedron calculator for edge length, surface area, volume, spherical radius, spherical edge radius and incircle radius

Individual evidence

1. ↑ Eric Weisstein: Dodecahedron. Umkugelradius, formula (17) further simplified. In: MathWorld Wolfram. A Wolfram Web Resource, accessed July 1, 2020 . 
2. ↑ Eric Weisstein: Dodecahedron. Edge ball radius, formula (19). In: MathWorld Wolfram. A Wolfram Web Resource, accessed July 1, 2020 . 
3. ↑ Eric Weisstein: Dodecahedron. In spherical radius, formula (15). In: MathWorld Wolfram. A Wolfram Web Resource, accessed July 1, 2020 . 
4. ↑ Harish Chandra Rajpoot: Solid angles subtended by the platonic solids (regular polyhedra) at their vertices. SlideShare, March 2015, accessed July 1, 2020 . 
5. ↑ Alternative expression for . ${\displaystyle \cos \Omega }$Wolfram Alpha, accessed July 1, 2020 . 
6. ↑ waldorfschule-muenster.de ( Memento from June 11, 2015 in the Internet Archive )
7. ↑ Eric Weisstein: Dodecahedron. Networks. In: MathWorld Wolfram. A Wolfram Web Resource, accessed July 1, 2020 . 
8. ↑ Mike Zabrocki: HOMEWORK # 3 SOLUTIONS - MATH 3260. (PDF) York University, Mathematics and Statistics, Toronto, 2003, p. 4 , accessed May 31, 2020 . 
9. ↑ Eric Weisstein: Dodecahedral Graph. Graph. In: MathWorld Wolfram. A Wolfram Web Resource, accessed July 1, 2020 .