Golden cut
The golden ratio ( Latin sectio aurea , proportio divina ) is the division ratio of a line or other size, in which the ratio of the whole to its larger part (also called major ) is equal to the ratio of the larger to the smaller part (the minor ). With a major and a minor, the following applies:
- or
The division ratio of the golden section calculated by dividing these quantities as a number is an irrational number , i.e. a number that cannot be represented as a fraction of whole numbers . This number is also known as the golden ratio or the golden number . As a mathematical symbol for this number, the Greek letter Phi ( , or ), more rarely tau ( , ) or is used:
Knowledge of the golden section has been proven in mathematical literature since ancient Greece ( Euclid of Alexandria). Occasionally in the late Middle Ages ( Campanus von Novara ) and especially then in the Renaissance ( Luca Pacioli , Johannes Kepler ) it was also placed in philosophical and theological contexts. Since the 19th century it has been assessed as an ideal principle of aesthetic proportioning, first in aesthetic theory ( Adolf Zeising ) and then also in artistic, architectural and handicraft practice. The verifiability of such a special aesthetic effect is, however, controversial in research, as is the historical question of whether the golden ratio also played a role in the proportioning of works of art and buildings from older epochs.
The relationship of the golden section is not only important in mathematics, art or architecture, but can also be found in nature, for example in the arrangement of leaves and in the inflorescences of some plants.
Definition and elementary properties
A section of the length is divided by an inner point so that the ratio of the length of the larger section to the length of the smaller section is equal to the ratio of the total section length to the length of the larger section. It is therefore respectively . This division is called the golden section of the route . One then speaks of the point dividing the line in the golden ratio or also of the constant division of the line through the point . The ratio of the route sections and is called the golden number .
A simple calculation shows:
If a route is divided according to the golden ratio, the longer section applies
and for the shorter one
The golden number is an irrational number , which means that it cannot be represented as a fraction of two whole numbers. However, it is an algebraic number of degree 2, in particular it can be constructed with a compass and ruler.
Furthermore, it is particularly difficult to approximate by fractures . For this reason it is sometimes referred to as the most irrational number in the literature . This property is explained in more detail in the section Approximation properties of the golden number .
Geometric statements
Construction method
According to the postulates of Euclid, only those methods are accepted as construction methods that are limited to the use of compasses and ruler (without a scale). There is an abundance of such methods for dividing a route in the ratio of the golden section, of which only a few are mentioned below as examples. A distinction is made between an inner and an outer division. In the case of the outer division , the point located on the outside in the extension of the initial route is sought, which makes the existing route the (larger) part of the golden section. The golden ratio represents a special case of harmonic division . In the following, two modern constructions found by artists are listed.
Inner division
Classic procedure with internal division, popular for its simplicity:
|
|

|
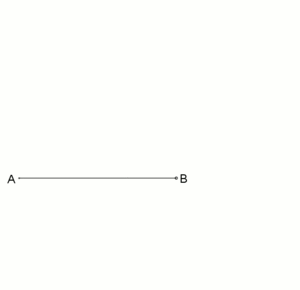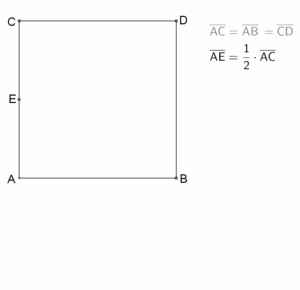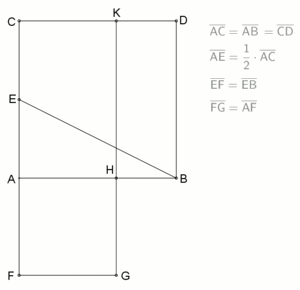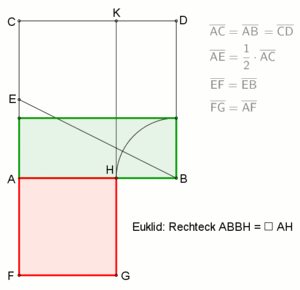
Inner division according to Euclid :
In 1781 Johann Friedrich Lorenz described the following task for Euclid in his book Euclid's Elements : "To cut a given straight line, AB, in such a way that the Rectangel from the whole and one of the sections is equal to the square of the other section." The result of the adjacent animation shows that the route is divided in a ratio that is now known as the golden ratio with internal division. A simplified construction, see left picture, has proven itself as a representation of this procedure:
|

|
Construction after the Austrian artist Kurt Hofstetter , which he published in the Forum Geometricorum in 2005 :
|
External division

|
Classic method with external division:
This method is z. B. used for the construction of the pentagon for a given side length . |

|
Construction after the American artist George Odom , which he discovered in 1982:
|
Instead of constantly having to redesign, artists and craftsmen in the 19th century used a golden circle - a reduction circle adjusted to the golden ratio . A similar instrument in the form of a cranesbill was used in the carpentry trade in particular .
The golden ratio in the pentagon and in the pentagram
The regular pentagon and pentagram each form a basic figure in which the relationship of the golden ratio occurs repeatedly. The side of a regular pentagon z. B. is in the golden ratio to its diagonals. The diagonals, in turn, share a golden ratio, i.e. i.e., behaves like to . The proof for this uses the similarity of suitably chosen triangles.
The pentagram, one of the oldest magical symbols in cultural history , is particularly closely related to the golden ratio. For every route and section in the pentagram there is a partner who is in the relationship of the golden ratio with it. In the illustration, all three possible pairs of routes are marked blue (longer route) and orange (shorter route). They can be generated one after the other using the continuous division method described above. In principle, it can be continued into the reduced pentagram that could be drawn in the inner pentagon, and thus in all others. If the two lines were in a ratio of whole numbers, this method of continued subtraction would have to yield zero at some point and thus break off. However, a look at the pentagram clearly shows that this is not the case. A further development of this geometry can be found in the Penrose tiling .
To prove that it is the golden ratio, note that in addition to the many routes, which are of the same length for obvious reasons of symmetry, also applies. The reason is that the triangle has two equal angles, as can be recognized by shifting the line parallel , and is therefore isosceles. According to the theorem of rays :
If it is replaced and the equality of the occurring parts is observed, then exactly the above definition equation for the golden ratio is obtained.
Golden rectangle and golden triangle
A rectangle whose aspect ratio corresponds to the golden ratio is called a golden rectangle and an isosceles triangle with two sides in this ratio is called a golden triangle .
- To compare rectangular proportions, see the section Comparing with other prominent aspect ratios.
- A golden triangle is part of the Inner Division method in the Construction Techniques section .
Golden angle

The golden angle is obtained when the full angle is divided in the golden ratio. This leads to the truncated angle , but its complement to the full angle is usually referred to as the golden angle. This is justified by the fact that rotations around do not play a role and the sign only indicates the direction of rotation of the angle.
By repeated rotation around the golden angle, new positions arise again and again, for example for the leaf roots in the picture. As with any irrational number, there will never be exact overlaps. Because the golden number represents the “most irrational” number in the sense described below , it is achieved that the total overlap of the leaves, which hinders photosynthesis , is minimized.
The first positions divide the circle into sections . These cutouts have a maximum of three different angles. In the case of a Fibonacci number , there are only two angles . For the angle is added.
If one looks at the refining decompositions of the circle for progressive growth, then the -th position always divides one of the remaining largest sections, namely always the one that emerged first in the course of the divisions, i.e. H. the "oldest" section. This division takes place in the golden ratio, so that, seen in clockwise direction, an angle with an even line is before an angle with an odd one .
If we denote the section with the angle with , then we get the circle decompositions one after the other , etc.
Golden spiral

The golden spiral is a special case of the logarithmic spiral . This spiral can be constructed by recursively dividing a golden rectangle into a square and another, smaller golden rectangle (see adjacent picture). It is often approximated by a sequence of quarter circles. Your radius changes by the factor with every 90 ° rotation .
It applies
with the slope , with the numerical value for the right angle , i.e. 90 ° or , i.e. with the golden number .
The following applies to the slope:
The golden spiral is distinguished among the logarithmic spirals by the following property. Let there be four successive intersections on the spiral with a straight line through the center. Then the two pairs of points and are harmonically conjugated , i.e. i.e., applies to their double ratio
Golden ratio in the icosahedron

The twelve corners of the icosahedron form the corners of three equal-sized, perpendicular rectangles with a common center and with the aspect ratios of the golden section. This arrangement of the three rectangles is also called the golden ratio chair. Because the icosahedron is dual to the pentagonal dodecahedron, the twelve centers of the pentagons also form the corners of a golden section chair.
Mathematical properties
Derivation of the numerical value
Algebraic
The definition given in the introduction
reads with the right side resolved and after conversion
or with as follows:
Multiplication by gives the quadratic equation
with the two solutions and
Since of these two values only the positive one is possible for the golden number, it follows
Geometric
The approach is the definition given in the introduction
with a major .
On a straight line , the numerical value is first designated as a point and then the major is plotted as a numerical value , resulting in the point of intersection . After the erection of the solder onto the track in is from the point the distance plotted on the solder, there arises the intersection Halves is now in it generates the numerical value of the points and are vertices of the right-angled triangle with the short sides and
Using the Pythagorean theorem
one thus obtains the hypotenuse
Finally, you need an arc around (numerical value ) with the radius that intersects the numerical line in , shows the minor as a line and provides the numerical value .
The numerical value of can thus be read directly on the numerical line:
In summary, it also results
The golden number sequence
| 4th | ≈ 6.854 | |
| 3 | ≈ 4.236 | |
| 2 | ≈ 2.618 | |
| 1 | ≈ 1.618 | |
| 0 | = 1,000 | |
| −1 | ≈ 0.618 | |
| −2 | ≈ 0.382 | |
| −3 | ≈ 0.236 | |
| −4 | ≈ 0.146 |
A sequence for can be constructed for a given number . This sequence has the property that every three consecutive links form a golden ratio, that is, it applies
- as well as for everyone
This sequence plays an important role in the theory of proportions in art and architecture, because further harmonious lengths can be created for a given length . This means that objects of very different dimensions, such as window and room width, can be related using the golden ratio and entire series of harmonious dimensions can be created.
It is worth mentioning that the decimal places for , and do not differ because they are positive and the difference between them is an integer. The number after the decimal point is always x, 618.033.988.75 ... with x = 0, 1, 2.
Relation to the Fibonacci numbers
| Deviation from in% |
|||
|---|---|---|---|
| 1 | 1 | = 1.0000 | −38 |
| 1 | 2 | = 2.0000 | +23 |
| 2 | 3 | = 1.5000 | −7.3 |
| 3 | 5 | ≈ 1.6667 | +3.0 |
| 5 | 8th | = 1.6000 | −1.1 |
| 8th | 13 | = 1.6250 | +0.43 |
| 13 | 21st | ≈ 1.6154 | −0.16 |
| 21st | 34 | ≈ 1.6190 | +0.063 |
| 34 | 55 | ≈ 1.6176 | −0.024 |
| 55 | 89 | ≈ 1.6182 | +0.0091 |
| 89 | 144 | ≈ 1.6180 | −0.0035 |
| 144 | 233 | ≈ 1.6181 | +0.0013 |
The infinite sequence of Fibonacci numbers is closely related to the golden ratio (see the sections Middle Ages and Renaissance below ):
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
The next number in this sequence is obtained as the sum of the two preceding ones. The ratio of two consecutive numbers in the Fibonacci sequence goes against the golden ratio (see table). The recursive law of formation means namely
If this ratio converges to a limit value , this must apply
This reasoning also applies to generalized Fibonacci sequences with any two initial terms.
The terms of the Fibonacci sequence can be calculated for all of them using Binet's formula:
With
This formula delivers the correct initial values and and satisfies the recursive equation for all with .
Approximation properties of the golden number
As already stated above, the golden number is an irrational number, that is, it cannot be represented as a fraction of two whole numbers. It is sometimes called the "most irrational" of all numbers because it is particularly difficult to approximate (in a special number-theoretical sense) by rational numbers ( Diophantine approximation ). This will be illustrated in the following by a comparison with the likewise irrational circle number . The latter can be approximated much better than , for example, the fraction can be approximated with a deviation of only about 0.00126. Such a small error would generally only be expected with a much larger denominator.
The golden number can be constructed directly from the requirement for the poorest possible approximability using rational numbers. To understand this, consider the following procedure for approximating any number by a fraction using the number as an example . Initially, this number is divided in its integer fraction and a residue which is smaller than is . The reciprocal of this remainder is a number that is greater than . So they can in turn be separated into an integer part and a remainder less than : . If you do the same with this remainder and all the following, then the infinite continued fraction expansion follows the number
If this continued fraction expansion stopped after a finite number of steps, then for the known approximations , , , get, ..., facing rapidly seek. For every single one of these fractions, there is no fraction with a denominator of at most the same size that approximates better. This is very general:
- If the continued fraction expansion of an irrational number is terminated at any point, the result is a rational number which approximates optimally among all rational numbers with a denominator .
In the continued fraction above, a whole number appears in front of each plus sign. The larger this number, the smaller the fraction in whose denominator it is, and therefore the smaller the error that arises when the infinite continued fraction is broken off before this fraction. The largest number in the section of the continued fraction above is the . This is why is such a good approximation for .
In reverse of this line of argument, it follows that the approximation is particularly bad if the number in front of the plus sign is particularly small. The smallest permitted number there is, however . The continued fraction, which contains only ones, can therefore be approximated particularly poorly by rational numbers and in this sense is the “most irrational of all numbers”.
For the golden number, however, applies (see above), which results from repeated application
Since the continued fraction expansion of the golden number contains only ones, it belongs to those numbers that are particularly difficult to rationally approximate. If your continued fraction development breaks off at any point, a fraction of two consecutive Fibonacci numbers is always obtained.
Another curious designation is the following: In the theory of dynamic systems , numbers whose infinite continued fraction only contains ones from any point on are called “ noble numbers ”. Since the golden number has only ones in its continued fraction, it can (jokingly) be called the “noblest of all numbers”.
From an algebraic number theoretic point of view
The golden section is an algebraic number as the zero of the polynomial . Because the polynomial is normalized and all coefficients are integers, the golden ratio is even whole . Suppose that then is a field expansion of degree 2. This is a square number field . It is the real-square number field with the smallest discriminant, namely 5 (the real-square number field with the next largest discriminant is 8 with discriminant). Let it be the associated wholeness ring . Because it is whole, it is true , but more than that: Because of
the golden ratio is even a unit of the whole ring . Its multiplicative is the inverse . This can also be shown algebraically simply by knowing the minimal polynomial :
However, the golden ratio is not only a unit of the Whole Ring , but also a fundamental unit of the Whole Ring. This means that every element is shaped with . They also form a base of . This means that each element can be clearly written as with . A simple consequence of the next paragraph is that it also forms a base of . It is .
The entire edge points of the convex hull of , which are important, for example, for the desingularization of tips of Hilbert's module surfaces , are given by the even powers of . The fact that these edge points are all in , i.e. are all units, is equivalent to the singularity of the “infinite” resolution of the tip over this living rational curve in the Hilbert module area associated with the body .
Other mathematical properties
- The following infinite chain root can be derived from:
- The square and any higher integer power of can be represented as the sum of an integer multiple of and an integer multiple of 1. The fundamental importance of the golden ratio for quasi-periodic lattices ( see quasicrystal ) is based on this property .
- More precisely (where the -th is the Fibonacci number ).
A brief proof of this relationship is provided by the direct representation of the Fibonacci numbers using and :
as falls out;
the first assertion arises after dividing by . - With the analogous proof of the second assertion it falls out.
- From the trigonometry follows among other things
- and
- is the full acute angle and half of the obtuse outer angle of the pentagram . Occasionally the role of the golden ratio for the pentagon is referred to as being as important as that of the circle number for the circle.
- The golden ratio can also be expressed with the help of Euler's number and the hyperbolic area sine function :
- Substituting in the for valid geometric series formula results
- because .
- Applying the binomial theorem to the context gives:
- or: .
Generalization of the golden ratio
Geometric mean
If the length of the line is interpreted as a real number , and the division by the golden section in the point into the two sections and as a division of this number into two summands and , then the geometric mean of the numbers is and . This follows from the general definition of the geometric mean , in this case . Furthermore, it follows immediately that again is the geometric mean of and .
For any real one, a mathematical sequence can be given, both ascending and descending. Both the ascending and the descending order are defined recursively.
The following applies to the ascending sequence: with the starting point
The following applies to the descending order: with the starting point
Continuous division
The geometric generalization of the golden section through its multiple application is the continuous division of a line . The route is first broken down into a smaller route and a larger one . The route (i.e. the larger of the resulting route sections) is now subjected to a golden ratio again, leaving the (new) larger route section and the smaller one. This step can now be repeated an infinite number of times, since due to the mathematical properties of the golden section, despite the progressive division, there will be no point that coincides with the original point .
This generally applicable procedure can also be achieved by deleting the line at the point after the construction of : The point created in this way is the same as the point just described in the (general) decomposition .
This sequence of steps is called the continuous division of a route .
Analytically, the continuous division as a generalization of the golden ratio is an example of self-similarity : If the resulting lengths of the lines are interpreted as real numbers, then the following applies: If the shorter of the two lines is subtracted from the longer, an even shorter line is , to which is the mean distance in turn in the ratio of the golden ratio, that is
This statement is again analytically identical to the descending geometric sequence of the previous section. The same statement applies to the lengthening of a given distance, it leads to an ascending geometric sequence.
From this statement, however, the following also applies: A rectangle with the sides and corresponds to the golden ratio if this is also the case for the rectangle with the sides and . A golden rectangle can therefore always be broken down into a smaller golden rectangle and a square. This generalization is in turn the basis for the construction of the (infinite) golden spiral, as described above.
history
The term golden ratio was already used in 1717 by M. Johann Wentzel Kaschuben in his work Cvrsvs mathematicvs:… . In it, he describes a geometrical task (details in the section on the golden ratio as a construction element ), the solution of which requires this special division ratio. In conclusion, he noted: "The ancients call this the golden section."
The term golden ratio only became popular from the first half of the 19th century, although the mathematical principles had been known since ancient times. The term golden number also originates from this time, in 1819 this term was still associated with the Meton cycle in one of the Greek calendar systems .
Antiquity
The first exact description of the golden section that has survived can be found in the second book of the elements of Euclid (around 300 BC), who came across it through his investigations on the Platonic solids and the pentagon or the pentagram. His name for this division ratio was later translated into Latin as “proportio habens medium et duo extrema”, which is now referred to as “division in the inner and outer relationship”.
Today it can be considered historically certain that the golden ratio was already known before Euclid. It is disputed whether the discovery goes back to Hippasus of Metapontus (late 6th century BC) or to Eudoxus of Knidos (around 370 BC).
middle Ages
In his arithmetic book Liber abbaci (first version not preserved in 1202, second version not preserved before 1220), an extensive arithmetic and algebraic textbook on arithmetic with Indo-Arabic numerals, the Italian mathematician Leonardo da Pisa , called "Fibonacci", comes in short also to speak of the Fibonacci sequence, later named after him, in connection with the so-called rabbit task, in which it is to be calculated how many pairs of rabbits are present in total at a reproductive rate of a pair of young rabbits per parent pair and month after a year are when a first couple and their offspring have cubs from their second month of life in the first month. Leonardo presents the sequence of numbers for each month (2, 3, 5, 8 ... to 377) and points out that each term in the series (from the third) can be calculated by adding up the two preceding series elements. There is no further preoccupation with this episode, i. This means that it does not show the connection to the golden section.
The fact that he was aware of the (later so-called) golden ratio and was a term in the Euclidean tradition is shown towards the end of his work in an algebraic exercise in which the aim is (reproduced in a modern formulation) and finding with and .
Leonardo points out that in the case of the proportion applies, 10 is divided by and in the ratio of the golden ratio (without using this term) ("et scis, secundum hanc diuisionem, 10 diuisa esse media et extrema proportione; quia est sicut 10 ad maiorem partem, ita maior pars ad minorem ").
Renaissance
However, Leonardo did not yet establish a connection between the Fibonacci sequence and the golden ratio: The discovery that dividing a term of the Fibonacci sequence by the preceding term as an approximate value was ascribed to Johannes Kepler for a long time , but has also been able to do so more recently can already be proven in a handwritten note, with which a reader presumably from Italy commented on Euclid's theorem II.11 in the Euclid edition of Pacioli from 1509 in the first half of the 16th century:
“Sit linea from 233 pedum, divisa ut docet 11 huius in duo inaequalia in puncto h et sit bh portio eius maior 144 et ha portio eius minor 89. ducatur ab in ha et perveniunt 20737 et bh in se et perveniunt 20736. et sic cognosces quod in mutationibus non est laborandum quid impossibile est numerum ita dividi ut ista 11 proponit. similiter accidit si linea 13 pedum dividatur in lineam 8 pedum, et lineam 5. ”
"A straight line from 233 feet is, as Theorem 11 demonstrates here, divided into two unequal parts at a point h , and bh is its larger part with 144 and ha its smaller part with 89. ab is multiplied by ha , and you get 20737, and bh multiplied by itself, you get 20736. And from this you may see that there is no need to bother with substitutions to show that it is impossible to divide the number the way it is Theorem 11 is demonstrated here. The same thing happens if a straight line of 13 feet is divided into a straight line of 8 and a straight line of 5 feet. "
The editor of this Euclid edition, the Franciscan Luca Pacioli di Borgo San Sepolcro (1445–1514), who taught mathematics at the University of Perugia , had also dealt intensively with the golden ratio. He called this division of the route “divine division”, which referred to Plato's identification of creation with the five Platonic solids, for whose construction the golden ratio is an important aid. His work of the same name De divina proportione from 1509 consists of three independent books. The first is a purely mathematical treatise, but has no relation to art and architecture. The second is a short treatise on the writings of the Roman Vitruvius from the 1st century BC. About architecture, in which Vitruvius depicts the proportions of the human body as a template for architecture. This book contains a study by Leonardo da Vinci (1452–1519) of the Vitruvian Man . The ratio of the side of the square surrounding the person to the radius of the surrounding circle - not the ratio of the proportions of the person himself - in this famous picture corresponds to the golden ratio with a deviation of 1.7%, which is not mentioned in the accompanying book . In addition, this deviation would not be expected in a constructive process.
In October 1597, Johannes Kepler asked in a letter to his former Tübingen professor Michael Maestlin why there was only one possible solution to the task of constructing a right triangle in which the ratio of the shorter to the longer side was that of the longer to the longer Hypotenuse corresponds. On the original of this letter, Maestlin noted a calculation that put the hypotenuse once with 10 and once with 10,000,000, and for the latter case then the longer side as 7,861,514 and the shortest side as 6,180,340. This corresponds to an indication of the golden ratio that is accurate up to the sixth decimal place (and up to the fifth correct) and, according to the older sexagesimal calculations of antiquity, is the first known decimal indication of this type.
19th and 20th centuries
In treatises of various authors in the 19th century, in particular by the philosopher Adolf Zeising , the two writings of Pacioli and da Vinci were combined to the thesis that Pacioli had in the "De Divina Proportione" in collaboration with Leonardo da Vinci a connection between art and golden section produced and thus its rediscovery for the painting of the Renaissance founded. Zeising was also convinced of the existence of a natural law of aesthetics, the basis of which must be the golden ratio. He searched and found the golden ratio everywhere. His writings spread quickly and created a real euphoria about the golden ratio. On the other hand, an examination of the literature shows that before Zeising no one believed to recognize the golden ratio in the works of antiquity or the Renaissance. Corresponding finds are therefore more controversial among art historians today, as Neveux demonstrated in 1995.
One of the first established uses of the term golden ratio was in 1835 by Martin Ohm (1792–1872; brother of Georg Simon Ohm ) in a mathematics textbook. The name sectio aurea also only came into being at this time.
Gustav Theodor Fechner , a founder of experimental psychology , did indeed determine a preference for the golden ratio in studies with test subjects using rectangles. However, the results for the route division and for ellipses were different. Recent studies show that the result of such experiments depends heavily on the context of the performance. Fechner also found in measurements of pictures in various museums in Europe that the aspect ratios in portrait format are on average around 4: 5 and in landscape format around 4: 3 and thus differ significantly from the golden ratio.
At the end of the 20th century, the art historian Marguerite Neveux looked in vain for corresponding markings or construction marks under the color of original paintings that allegedly contained the golden ratio using X-ray analysis methods.
Occurrence in nature
biology
The most spectacular example of the golden ratio in nature can be found in the arrangement of leaves ( phyllotaxis ) and in the inflorescences of some plants . With these plants, the angle between two consecutive leaves divides the full circle of 360 ° in the ratio of the golden section, if the two leaf bases are brought into congruence by a parallel shift of one of the leaves along the plant axis. It is the golden angle of about 137.5 °.
The resulting structures are also called self-similar : In this way, a pattern from a lower structural level is reflected in higher levels. Examples are the sunflower , cabbage species , pine needles on young branches, cones , agaves , many palm and yucca species and the petals of the rose , to name just a few.
The cause is the desire of these plants to keep their leaves at a distance. It is assumed that they produce a special growth inhibitor at each leaf attachment , which diffuses in the plant stem - mainly upwards, but to a lesser extent also in a lateral direction . Certain concentration gradients develop in different directions . The next leaf develops at a point on the circumference where concentration is minimal. This creates a certain angle to the predecessor. If this angle were to divide the full circle in proportion to a rational number , then this leaf would grow in exactly the same direction as the previous leaf. The contribution of this sheet to the concentration of the inhibitor is just at its maximum at this point. Therefore an angle arises with a ratio that avoids all rational numbers. The number is now the golden number (see above). Since it has not been possible to isolate such an inhibitor so far, other hypotheses are also being discussed, such as the control of these processes in an analogous manner through concentration distributions of nutrients.
The benefit for the plant could be that in this way from above incident sunlight is used optimally (or water and air), a presumption that already Leonardo da expressed Vinci, or in efficient transportation by photosynthesis resulting carbohydrates in Phloemteil the vascular bundle down. The roots of plants show the golden angle less clearly. In other plants, leaf spirals with different angles appear. In some cactus species, an angle of 99.5 ° is observed, which corresponds to the variant of the Fibonacci sequence 1, 3, 4, 7, 11, .... In computer simulations of plant growth, these different behaviors can be provoked by a suitable choice of the diffusion coefficient of the inhibitor.
In many plants organized according to the golden ratio, so-called Fibonacci spirals develop in this context . Spirals of this type are particularly easy to recognize when the distance between the leaves is particularly small compared to the circumference of the plant axis. They are not formed from consecutive leaves, but from leaves spaced apart , where is a Fibonacci number. Such leaves are in close proximity, because the -fold of the golden angle is approximately a multiple of 360 °
where the next smaller Fibonacci number is to. Since each of the leaves between these two belongs to a different spiral, spirals can be seen. If greater than , the ratio of the next two Fibonacci numbers is smaller and vice versa. Therefore spirals to successive Fibonacci numbers can be seen in both directions. The direction of rotation of the two types of spiral is left to chance, so that both possibilities occur equally frequently.
Fibonacci spirals (which in turn are assigned to the golden ratio) in inflorescences, such as in sunflowers, are particularly impressive. There flowers, from which fruits later develop, sit close to one another on the strongly compressed, disc-shaped inflorescence axis, whereby each individual blossom can be assigned to its own circle around the center of the inflorescence. Fruits that follow one another in terms of growth are therefore spatially far apart, while direct neighbors again have a distance corresponding to a Fibonacci number. In the outer area of sunflowers 34 and 55 spirals are counted, with larger specimens 55 and 89 or even 89 and 144. The deviation from the mathematical golden angle, which is not exceeded in this case, is less than 0.01%.
The golden ratio can also be seen in radially symmetrical five-fold flowers such as the bellflower , the columbine and the (wild) hedge rose . The distance between the tips of the petals of the closest neighbors and those of the next but one is related, as is usual with a regular pentagon. This also applies to starfish and other animals with five-fold symmetry.
In addition, the golden ratio is also assumed to be the ratio of the lengths of successive stem sections of some plants, as is the case with the poplar . In the ivy leaf , too , the leaf axes a and b (see illustration) are roughly in proportion to the golden section. However, these examples are controversial.
In the 19th century, the view was widespread that the golden ratio was a divine law of nature and that it was also implemented in many ways in the proportions of the human body. In his book on the proportions of the human body, Adolf Zeising assumed that the navel divides body size in proportion to the golden section, and the lower section is in turn divided by the knee . Furthermore, the proportions of adjacent parts of the limbs, such as the upper and lower arm and the finger bones, seem to be roughly in this relation. However, a precise check reveals scattering of the ratios in the 20% range. The definition of how the length of a body part is to be exactly determined also often contains a certain amount of arbitrariness. Furthermore, this thesis still lacks a scientific basis. The view that these observations are merely the result of the targeted selection of neighboring pairs from a set of arbitrary sizes therefore largely dominates.
Railway resonances
It has long been known that the orbital times of some planets and moons are in the ratio of small whole numbers such as Jupiter and Saturn with 2: 5 or the Jupiter moons Io , Ganymede and Europe with 1: 2: 4. Such orbital resonances stabilize the orbits of the celestial bodies against minor disturbances in the long term. It was only discovered in 1964 that sufficiently irrational conditions, such as those that would exist, can have a stabilizing effect. Such tracks are called KAM tracks (see Kolmogorow-Arnold-Moser theorem ), the three letters standing for the names of the discoverers Andrei Kolmogorow , VI Arnold and Jürgen Moser .
Black holes
Contractible cosmic objects without a solid surface, such as black holes or the sun , have the paradoxical property of becoming hotter when they radiate heat (negative heat capacity ) due to their own gravity . With rotating black holes, a change from negative to positive heat capacity takes place from a critical angular momentum , whereby this tipping point depends on the mass of the black hole. In a -dimensional space-time , a metric comes into play, the eigenvalues of which are the zeros of the characteristic polynomial
surrender.
Crystal structures
The golden ratio also appears in the quasicrystals of solid state physics , which were discovered in 1984 by Dan Shechtman and his colleagues. These are structures with five-fold symmetry , from which, as Kepler already recognized, no strictly periodic crystal lattices can be built up, as is usual with crystals . The surprise was correspondingly great when X-ray structure analyzes found diffraction images with five-fold symmetry. Structurally, these quasicrystals consist of two different rhombohedral basic components with which the space can be filled without gaps, but without global periodicity ( Penrose tiling ). Both rhombohedra are composed of the same diamond-shaped side surfaces, which are, however, oriented differently. The shape of these diamonds can now be defined by the fact that their diagonals are in proportion to the golden ratio. Shechtman was awarded the Nobel Prize in Chemistry in 2011 for the discovery of quasicrystals .
Applications of the golden ratio
Golden ratio as a construction element
M. Johann Wentzel Kaschuben wrote the geometrical task described below and shown in a constructive manner in 1717.
“§.34. An equilateral in which the one standing on one thigh is perpendicular , so the thigh itself cuts in such a way as it is perpendicular to the rest. Lines cut in can be found in the following ways. [...] ”
We are looking for an isosceles triangle in which a given line and one side of the triangle are orthogonal to each other and the point divides this side in the ratio of the golden section.
Construction
description (based on the description of the original, Fig. 7 mentioned therein is on Tab. I Alg. Fig. 8)
First, the line with the freely selectable length is set up perpendicular to the straight line . The right-angled triangle follows in which the side lies on the straight line . The arc around with radius results in the point of intersection, the arc around with radius divides into the side in the golden section. Draw a circle around with radius yields intersection and an arc to radius Well erect a perpendicular to off until the arc in cuts. With is the geometric mean of the lengths of the two lines and is determined. A circular arc around with a radius intersecting the circle in this case results in the right triangle Finally, the distance is up to the straight line extends and around the just created intersection is a circular arc with a radius drawn until the straight line in cut.
In the isosceles triangle thus found , the point of the vertical divides the leg in the golden section.
Paper and image formats
In letterpress printing occasionally has the useful area of a page, the so-called set of mirrors , positioned so that the ratio of the gutter to the top web to outer web to base web as 2: 5: 8 behaved. 3 This choice of Fibonacci numbers approximates the golden ratio. Such a design is still recommended in parts of the specialist literature on book printing.
Comparison with other prominent aspect ratios
The following figure shows a comparison of different rectangles with prominent aspect ratios in the vicinity of Specifies the ratio of height to width and the corresponding numerical factor:
- 4: 3 - Traditional TV and bale size for wrapping paper. Also used on older computer monitors (e.g .: 1024 × 768 pixels ). This format goes back to Thomas Alva Edison , who set the format of the classic film image ( 35 mm film ) to 24 mm × 18 mm in 1889 .
- √ 2 : 1 - The aspect ratio for A4 sheets and related DIN / EN / ISO dimensions. Halving by a cut that halves the longer sides of the rectangle results in rectangles with the same aspect ratio.
- 3: 2 - aspect ratio for 35 mm film (36 mm × 24 mm).
- 16:10 - Some computer screens . At 1.6: 1, these almost fit the golden ratio.
- Φ: 1 - aspect ratio in the golden ratio . In the picture approximated with 144 × 89 pixels (theoretical error only 5 · 10 −5 ). The two neighboring rectangles 3: 2 and 5: 3 have - like the shown rectangle with 144: 89 - aspect ratios of consecutive Fibonacci numbers and therefore also approximate the golden ratio comparatively well.
- 5: 3 - Used as a cinema film format along with many others .
- 16: 9 - widescreen television .
architecture
Early references to the use of the golden ratio come from architecture. The writings of the Greek historian Herodotus on the Cheops pyramid are sometimes interpreted in such a way that the height of the side surface to half the base edge would be in the ratio of the golden section. The corresponding text passage can, however, be interpreted. On the other hand, the thesis is also put forward that the ratio of pyramid height to base edge reflects the actual dimensions even better. The difference between the two theses presented is only 3.0%, but this does not mean absolute proof in favor of one or the other thesis.
Many works of ancient Greece are seen as examples of the use of the golden ratio, such as the front of the 447-432 BC. Parthenon temple built under Pericles on the Acropolis of Athens . Since no plans have survived for these works, it is not known whether these proportions were chosen consciously or intuitively. Possible examples of the golden ratio can also be found in later epochs, such as the Cathedral of Florence , Notre Dame in Paris or the gate hall in Lorsch (770 AD). In these cases, too, the deliberate application of the golden ratio cannot be proven on the basis of historical sources.
As a result, there is no empirically reliable evidence of a significantly higher frequency of the golden section in these epochs compared to other division ratios. There is also a lack of historical evidence for an intentional use of the golden ratio.
The old town hall in Leipzig , a Renaissance building from the years 1556/57, is mentioned again and again as an example of the implementation of the golden section . The town hall tower, which has moved out of the central axis, is, it is claimed, regarded as an architectural avant-garde achievement of the time and with the uproar it caused it represented the urban self-confidence of the city. Whereby it is not the middle of the town hall tower, as one might suspect at first glance, that divides the housing front in the golden ratio, but the somewhat offset middle of the main gate. At the same time, there is no evidence of this on detailed historical source research. In particular, there is no evidence that Hieronymus Lotter, as the master builder at the time, deliberately used the golden ratio as a construction principle: All the original sources only refer to a previous Gothic building on whose foundations Lotter built the town hall. There is no historical source evidence that the golden ratio played a role here.
The first historically proven use of the golden ratio in architecture dates back to the 20th century: the architect and painter Le Corbusier (1887–1965) developed a uniform system of measurement based on human measurements and the golden ratio from 1940. He published this in 1949 in his work Der Modulor , which is counted among the most important writings in architectural history and theory. As early as 1934, the University of Zurich awarded him the title of doctor honoris causa for the mathematical sciences for the application of mathematical principles of order . However, for the reasons outlined above, this is not evidence of previous use of this system.
Visual arts
Image composition
To what extent the use of the golden ratio in art leads to particularly aesthetic results is ultimately a question of the prevailing understanding of art. There is no reliable evidence for the general thesis that this proportion is perceived as particularly appealing and harmonious. Many artists consciously use the golden ratio, with many works art historians only found what they were looking for afterwards. However, given the plethora of possible structures found in a richly textured painting, these findings are often controversial.
Numerous sculptures by Greek sculptors , such as the Apollo of Belvedere , who is attributed to Leochares (around 325 BC), or works by Phidias (5th century BC) are seen as examples of the use of the golden ratio. The name for the golden ratio, which is often used today and was introduced by the American mathematician Mark Barr , also refers to the latter . The term , which is also occasionally used , however, refers to the Greek word τομή for "cut".
The golden ratio is also suspected in many works by Renaissance artists, including Raphael , Leonardo da Vinci and Albrecht Dürer , in Dürer's works in particular in his self-portrait from 1500 and his copper engraving Melencolia I from 1514.
The golden ratio is also used in photography for image design. The rule of thirds is used as a rule of thumb .
Contemporary visual arts
In contemporary fine arts, the golden ratio is not only used as a design feature, but is also a subject or central image content in some works. The artist Jo Niemeyer uses the golden ratio as a fundamental design principle in his works, which are assigned to concrete art . The artist Martina Schettina addresses the golden ratio in her work on the pentagon, in which the diagonals share the golden ratio. It also visualizes the construction method and formulas for the golden ratio.
Acoustics and music
Intervals
In music , tones are perceived as consonant when the ratio of their vibrational frequencies is a fraction of small whole numbers. The fact that an approximation of this ratio to the golden ratio does not necessarily lead to a melodious interval can be seen from the fact that among the tone intervals whose vibration ratio corresponds to successive Fibonacci numbers, at most the fifth with a vibration ratio of 3: 2 protrudes. The major third with a vibration ratio of 5: 4 is perceived as more harmonious than the major sixth with 5: 3 and the minor sixth with 8: 5. Since a tone interval in the golden ratio is about 833.09 cents, only about 19 cents larger than a minor sixth, it is difficult for an untrained ear to distinguish it from this ( ).
composition
The golden ratio is sometimes suspected in the structural concepts of pieces of music. The Hungarian musicologist Ernő Lendvai tried to prove the golden ratio as an essential design principle of Béla Bartók's works . In his opinion, Bartók designed the structure of his compositions in such a way that the number of bars in individual sections of the shape form ratios that would approximate the golden ratio. However, his calculations are controversial.
In music after 1945 there are examples of conscious proportioning according to the numbers of the Fibonacci sequence, for example in piano piece IX by Karlheinz Stockhausen or in the spectral music by Gérard Grisey .
Instrument making
The golden ratio is occasionally used in musical instrument making. Especially when it comes to violin making , it should guarantee instruments that are particularly beautiful. It is also claimed that the famous violin maker Stradivari used the golden ratio to calculate the sonically optimal position of the f-holes for his violins . However, these claims are based solely on subsequent numerical analysis of Stradivari's instruments. However, there is no evidence that Stradivarius consciously used the golden ratio to determine their proportions.
Computer science
Data structures
In computer science, data is stored in hash tables for quick access. The position at which a data record is saved in the table is calculated using a hash function . For efficient access, the data records must be written in the table as evenly as possible. A variant for the hash function is the multiplicative method , in which the hash values for a table of size are calculated according to the following formula:
Here, make Gaußklammern is that round the clip content to the nearest whole number. The respected computer scientist Donald E. Knuth suggests the freely selectable constant in order to obtain a good distribution of the data sets.
Procedure of the golden section
The golden section method (also: golden section method , golden section method or golden section search method ) is a method of mathematical non-linear optimization , more precisely it algorithmically calculates a numerical approximation for an extreme point (minimum or maximum) of a real function of a Variables in a search interval . It is based on the analytical application of the originally geometrically defined continuous division . In contrast to the interval halving procedure, the search interval is not halved with each step, but is reduced according to the principle of the golden ratio.
The parameter used ( tau ) does not have the value, as in the bisection process, but is selected so that two points and for the optimization process result that divide the search interval in the golden ratio.
If it is assumed that every point in every interval can be an extreme point with the same probability, in the case of indeterminacy intervals this leads to the method of the golden ratio z. B. 14% more effective than the interval halving method. In comparison to this and other sequential processes, it is - mathematically speaking - the most effective process for general functions; only in the case of differentiable functions is it inferior to the direct mathematical solution. The fact that this procedure did not prevail in manual calculations is mainly due to the necessary root calculations for the individual intermediate steps.
Others
Another connection between information theory and the golden section was made by Helmar Frank with the definition of conspicuousness . He was able to show that the mathematical value of the maximum conspicuousness comes very close to the ratio of the golden section.
See also
literature
Historical literature
- Luca Pacioli ; Constantin Winterberg (ed. And transl.): De divina proportione. Venice 1509. Carl Graeser, Vienna 1889 (in the Internet archive: Online , with alo: Online. )
- Adolf Zeising: New doctrine of the proportions of the human body. Rudolph Weigel, Leipzig 1854 (at Google Books. )
- Adolf Zeising: The normal ratio of chemical and morphological proportions. Rudolph Weigel, Leipzig 1856 (at Google Books. )
- Gustav Theodor Fechner : On experimental aesthetics. Hirzel, Leipzig 1871.
Newer literature
- Albrecht Beutelspacher , Bernhard Petri: The golden ratio. Spectrum, Heidelberg / Berlin / Oxford 1996. ISBN 3-86025-404-9 .
- Priya Hemenway: Divine Proportion. Phi in Art, Nature and Science. Sterling, New York 2005, ISBN 1-4027-3522-7 . (Priya Hemenway: The Secret Code: The puzzling formula that determines art, nature and science . Taschen Verlag, Cologne 2008, ISBN 978-3-8365-0708-0 . )
- Roger Herz-Fischler: A mathematical History of the Golden Ratio. Dover Publications, New York 1998, ISBN 0-486-40007-7 .
- Jürgen Fredel: Made-to-measure aesthetics. Studies on questions of proportion and the golden section. Lit, Hamburg 1998, ISBN 3-8258-3408-5 .
- Albert van der Schoot: The story of the golden section. The rise and fall of divine proportion. Frommann-Holzboog, Stuttgart 2005, ISBN 3-7728-2218-5 .
- Susanne Deicher: Review by: Albert van der Schoot: The history of the golden section. In: Sehepunkte 5 (2005), No. 12 [15. December 2005], web link.
- Hans Walser: The golden ratio. Teubner, Stuttgart 1993. ISBN 3-8154-2511-5 .
- Georg Markowsky: Misconceptions about the Golden Mean. (PDF; 2.05 MB). The College Mathematics Journal, Volume 23, Issue 1, January 1992.
- Clement Falbo: The Golden Ratio: A Contrary Viewpoint. (PDF; 625 kB). The College Mathematics Journal, Volume 36, Issue 2, March 2005.
Web links
German
- Marcus Frings: Golden Ratio. In: RDK. Laboratory (2015).
- Bernhard Peter: Golden Ratio - Mathematics and Meaning. (34 different construction methods, importance in art; private side).
- Ruben Stelzner: The golden ratio - the mystery of beauty. (2002).
- Images about the golden ratio in biology (private site).
- Joachim Mohr: The constant division or the golden section and the construction of the regular pentagon.
English
- Marcus Frings: The Golden Section in Architectural Theory. In: Nexus Network Journal. 4/1 (2002).
- Eric W. Weisstein : Golden Ratio . In: MathWorld (English).
- John J. O'Connor, Edmund F. Robertson : The Golden Ratio. In: MacTutor History of Mathematics archive .
- Alexander Bogomolny: Golden Ratio. On: cut-the-knot.org.
- Steven Strogatz : Proportion Control. New York Times (Online), September 24, 2012.
- Sequence A001622 in OEIS (decimal expansion of Φ)
- Episode A028259 in OEIS (Engel development of Φ)
- Episode A118242 in OEIS (Pierce development of 1 / Φ)
Individual evidence
- ↑ Schülerduden - Mathematik I. Duden-Verlag, 8th edition, 2008, ISBN 978-3-411-04208-1 , pp. 171-174.
- ↑ a b W. Gellert u. a .: Small encyclopedia of mathematics. VEB Bibliographisches Institut, Leipzig 1979, p. 184.
- ↑ Ben Green : Irrational and Transcendental Numbers. In: Timothy Gowers , June Barrow-Green , Imre Leader: The Princeton Companion to Mathematics. Princeton University Press 2008, ISBN 978-0-691-11880-2 , p. 222 ( excerpt (Google) ).
- ^ Johann Friedrich Lorenz : Euclid's elements, fifteen books . Ed .: In the publishing house of the bookstore des Waysenhauses. Hall 1781, S. 31 ff . ( Euclid's Elements, Book Two , The 11th Movement. A given straight line, AB, so to intersect… [accessed December 19, 2016]).
- ^ Forum Geometricorum Volume 5 (2005) 135-136. (PDF; 26 kB).
- ↑ Stanisław Świerczkowski: On successive settings of an arc on the circumference of a circle. In: Fundamenta Mathematicae. 46.2, 1958, pp. 187-189.
- ^ Tony van Ravenstein: Optimal Spacing of Points on a Circle. In: The Fibonacci Quaterly. 27, 1989, pp. 18-24, mathstat.dal.ca (PDF).
- ↑ Forum Geometricorum Volume 16 (2016) 429-430 (PDF).
- ↑ The deviation occurring here is approximately 16 times smaller than that guaranteed by Dirichlet's approximation theorem (namely ). In contrast, when approximating through , the deviation is only 2.2 times smaller than .
-
^ A) Serge Lang : Introduction to Diophantine Approximations. Springer-Verlag 1995, p. 9.
b) Ivan Niven , Herbert S. Zuckermann, Hugh L. Montgomery: An Introduction to the Theory of Numbers. Wiley, 1960, 5th edition 1991, ISBN 0-471-54600-3 , p. 338 (Theorem 7.13).
It should be noted, however, that this theorem does not exclude that there are other best approximations besides these fractions . For example, the number approximates better than 3 and approximates better than . - ^ Golden ratio. Encyclopedia of Mathematics .
- ^ IN Bronstein, KA Semendjajew: Taschenbuch der Mathematik. 20th edition, joint edition Verlag Nauka Moscow and BSB BG Teubner Verlagsgesellschaft, Leipzig 1981, p. 167.
- ↑ M. Johann Wentzel Kaschuben: Cvrsvs mathematicvs, or clearer term of the mathematical sciences. Bey JF Bielcken, 1717, p. 2 , accessed April 15, 2020 .
- ^ A b M. Johann Wentzel Kaschuben: Cvrsvs mathematicvs, or clearer term of the mathematical sciences. Bey JF Bielcken, 1717, p. 566 , accessed April 15, 2020 .
- ↑ Steven Bradley: The golden section revisited: magic or myth?
- ↑ General German real encyclopedia for the educated classes. In ten volumes. Fourth volume (G and H). Fifth original edition, FA Brockhaus, Leipzig 1819, p. 296.
- ^ A b John J. O'Connor, Edmund F. Robertson : The Golden ratio. In: MacTutor History of Mathematics archive .
- ^ Rudolf Haller: Elements of Euclid. Edition Opera Platonis 2010, Book II, Movement 11 (PDF).
- ↑ If it is true that Hippasus discovered irrationality on the pentagon (and not on the square), then he would also be the inventor of the golden ratio. But since that is exactly what is controversial - see Leonid Zhmud (1997) p. 174 f. (argues for the square) and Kurt von Fritz : Grundprobleme der Geschichte der Antique Wissenschaft, Berlin 1971, pp. 564–569 (argues for the pentagon); Dirk Stegmann makes a very convincing case for Hippasos in The Golden Section (PDF; 666 kB), p. 10 . Otherwise, Eudoxos, with his research on proportionality and as a verifiable source of ideas for Euclid, is then to be regarded as the inventor.
- ↑ Leonardo da Pisa: Liber abbaci. (Cap. I, 7, there among other tasks: Quot paria coniculorum in uno anno ex uno pario germinentur ), ed. by Baldassare Boncompagni, Scritti di Leonardo Pisano matematico del secolo decimoterzo, Volume I, Roma: Tipografia delle scienze matematiche e fisiche, 1857, p. 283 f., reproduction of the Florence manuscript, Cod.magliabechiano cs cI, 2626, fol. 123v – 124r, with Heinz Lüneburg: Leonardi Pisani Liber Abbaci or reading pleasure of a mathematician. 2. revised and exp. Edition, Mannheim a. a .: BI Wissenschaftsverlag, 1993, ISBN 3-411-15462-4 , after p. 252; Rendering of rabbit duty & Latin text. a. from Bernd Thaller: Leonardo and the golden ratio. (PDF; 3.02 MB) June 30, 2017, with English translation by Roberto Bignoni, The Golden Number - 3 -.
- ^ Formalized reproduction after Heinz Lüneburg: Leonardi Pisani Liber Abbaci or reading pleasure of a mathematician. 2. revised and exp. Edition, Mannheim a. a .: BI Wissenschaftsverlag, 1993, ISBN 3-411-15462-4 , p. 298.
- ↑ Leonardo da Pisa: Liber abbaci. Cap. 15, ed. Boncompagni p. 438, to be found in the reproduction of cap. 15 by Guillaume Libri: Histoire des sciences mathématiques in Italie. Volume II, Paris: Jules Renouard et C.ie, 1838, p. 430 ( excerpt in the Google book search)
- ↑ Leonard Curchin, Roger Herz-Fischler: De quand date le premier rapprochement entre la suite de Fibonacci et la division en extrême et moyenne raison? In: Centaurus. 28,2 (1985), pp. 129-138, especially p. 130.
- ↑ Roger Herz-Fischler: A mathematical History of the Golden Ratio. Dover Publications, Minneola (New York) 1998, p. 158 (Section 31.J.iii).
- ^ A b Adolf Zeising: New doctrine of the proportions of the human body . Rudolph Weigel, Leipzig 1854, p. 264 .
- ^ A b Marguerite Neveux, HE Huntley: Le nombre d'or. Radiography d'un mythe suivi de La Divine Proportion . Ed. du Seuil, 1995, ISBN 978-2-02-025916-3 .
- ↑ Martin Ohm: The pure elementary mathematics Vol II: The level room size theory . Jonas Verlagbuchhandlung, Berlin 1835, p. 194 .
- ↑ Gustav Theodor Fechner: Preschool of aesthetics . Breitkopf & Härtel, 1876, p. 190 .
- ↑ Camillo Sitte : About the practical value of the doctrine of the golden section. In: Camillo Sitte: Writings on art theory and art history. Böhlau 2010, ISBN 978-3-205-78458-6 , pp. 435-446, esp. 438-439 ( excerpt (Google) ).
- ↑ Underwood Dudley: The Power of Numbers: What Numerology Takes Us To Believe. Gabler 1999, ISBN 3-7643-5978-1 , pp. 243-245 ( excerpt (Google) ).
- ^ Marguerite Neveux: "Le nombre d'or est une affabulation". In: LaRecherche.fr. Archived from the original on September 4, 2013 ; Retrieved November 1, 2011 .
- ↑ See Dvorak / Freistetter / Kurths: Chaos and stability in planetary systems. (Springer Lecture Notes in Physics, 2006), pp. 118–121 and the Wikipedia article on noble numbers .
- ^ Remo Badii, A. Politi: Complexity: Hierarchical Structures and Scaling in Physics. Cambridge University Press 1999, ISBN 0-521-66385-7 , p. 46 ( excerpt (Google) ).
- ^ Marcus Chown : The golden rule - It links art, music and even architecture. Marcus Chown on an enigmatic number. The Guardian , January 16, 2003, accessed December 31, 2013 .
- ^ JA Nieto: A Link Between Black Holes and the Golden Ratio . In: Cornell University . June 2, 2011. arxiv : 1106.1600 .
- ^ D. Shechtman, I. Blech, D. Gratias, JW Cahn: Metallic phase with long range orientational order and no translation symmetry . In: Physical Review Letters . tape 53 (20) , 1984, pp. 1951-1954 .
- ^ The Nobel Prize in Chemistry 2011 - Scientific Background. Nobelprize.org, May 6, 2012, accessed May 6, 2012 .
- ^ The Nobel Prize in Chemistry 2011. Nobelprize.org, May 2, 2012, accessed May 2, 2012 .
- ↑ M. Johann Wentzel Kaschuben: Cvrsvs mathematicvs, or clearer term of the mathematical sciences. P. 564, accessed April 15, 2020.
- ↑ M. Johann Wentzel Kaschuben: Cvrsvs mathematicvs, or clearer term of the mathematical sciences. Tab. I Alg., Accessed on April 17, 2020.
- ↑ Horst Knietzsch: Film - yesterday and today: Thoughts and dates on 7 decades of the history of film art. Urania, Leipzig 1967, snippet view on Google Books.
- ↑ For this z. B. Old Town Hall in Leipzig Lexicon with further evidence. Last accessed on June 3, 2012.
- ^ Mario Livio: The golden ratio: The story of phi, the world's most astonishing number . Broadway Books, 2003, ISBN 978-0-7679-0816-0 , pp. 177-178 .
- ^ Mario Livio: The golden ratio: The story of phi, the world's most astonishing number . Broadway Books, 2003, ISBN 978-0-7679-0816-0 , pp. 5 .
- ↑ Michael Frye: Digital Landscape Photography: Photography like Ansel Adams and Co. Hüthig Jehle Rehm 2010, ISBN 978-3-8266-5896-9 , p. 72 ( excerpt in the Google book search).
- ↑ Garry Reynolds: Zen or the art of presentation: design and present with simple ideas. Pearson Education 2008, ISBN 978-3-8273-2708-6 , pp. 151-152 ( excerpt (Google) ).
- ↑ Bernhard Peter: The golden ratio in the concrete art: Examples from Jo Niemeyer. On: welt-der-wappen.de. Retrieved November 1, 2011.
- ↑ Pictures in the virtual math museum of the TU Freiberg.
- ^ Maths Museum TU Freiberg.
- ↑ Helmut Reis: The golden section and its meaning for harmony (= Orpheus series on basic questions in music 54 ). Verlag für Systematic Musikwissenschaft, 1990, ISBN 978-3-922626-54-1 .
- ^ Jonathan Kramer: The Fibonacci Series in Twentieth-Century Music . In: Journal of Music Theory . tape 17 , no. 1 , 1973, p. 110-148 .
- ↑ How a Violin is Made. In: Popular Mechanics. September 1943, pp. 106-108 ( excerpt (Google) ).
- ↑ Stewart Pollens: Stradivari. Cambridge University Press, 2010, ISBN 978-0-521-87304-8 , p. 239 ( excerpt (Google) ).
- ↑ Thomas H. Cormen, Charles Leiserson , Ronald Linn Rivest , Clifford Stein: Introduction to Algorithms. 2nd Edition. MIT Press, 2001, ISBN 0-262-53196-8 , pp. 231-232.
- ^ Markos Papageorgiou, Marion Leibold, Martin Buss: Optimization . 4th edition. Springer-Verlag, Berlin / Heidelberg 2015, p. 30 , doi : 10.1007 / 978-3-662-46936-1 .
- ↑ Florian Jarre, Josef Stoer: Optimization. Springer, Berlin 2004, ISBN 3-540-43575-1 , pp. 130 ff. ( Excerpt (Google) ).
- ↑ W. Gellert et al. a .: Small encyclopedia of mathematics. VEB Bibliographisches Institut Leipzig, 1979, p. 694.
- ↑ Horst Völz : Reproduction 11/11/2006: Computer und Kunst series akzent 87. 2nd edition. Urania-Verlag Leipzig Jena - Berlin 1990. (PDF); The surprise value. (PDF) p. 14 of 67; accessed on August 13, 2018.
- Albrecht Beutelspacher , Bernhard Petri: The golden ratio. Spectrum, Heidelberg / Berlin / Oxford 1988, ISBN 3-411-03155-7 .








































































































































































































![{\ displaystyle {\ bar {x}} _ {\ text {geom}} = {\ sqrt [{n}] {x_ {1} \ cdot x_ {2} \ dotsm x_ {n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8218f179881c3afe5663221e4b86c0c60bdd94b0)
![{\ displaystyle x = {\ sqrt [{2}] {a (ax)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e155c4db85203c7f8d4366d8030b50851e8d6085)







































































![[from]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)








