Parallel shift

Example of a translation

The parallel shift or translation is a geometric mapping that shifts every point of the plane of the drawing or space in the same direction by the same distance. It can be identified by a vector , the so-called displacement vector .

Parallel displacements are part of the movements , since lengths and angles are retained when they are used. As movements, they - especially the parallel displacements in the plane - are also counted among the congruence maps.

The concept of parallel displacement can be generalized from the two- or three-dimensional visual space into the n-dimensional Euclidean space and even further into the Riemannian geometry or the affine geometry .

Two-dimensional viewing space

Parallel displacement of a triangle

In two-dimensional (Euclidean) space , a parallel shift is a mathematical function that shifts every point in space by the same distance in the same direction. A parallel shift is thus given by an affine linear function ${\displaystyle \mathbb {R} ^{2}}$

${\displaystyle s\colon \mathbb {R} ^{2}\to \mathbb {R} ^{2}}$

With

${\displaystyle s(x):=x+a}$,

where applies, described. ${\displaystyle a\in \mathbb {R} ^{2}}$

Riemannian geometry

Parallel transport of a vector along a curve on a spherical surface.

→ Main article : parallel transport

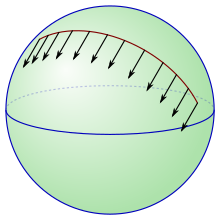
In Riemannian geometry , the concept of parallel displacement from Euclidean geometry is generalized to curved objects such as the surface of a sphere. Mathematically precisely, these curved objects are defined as Riemannian manifolds . Vectors at these manifolds can be shifted in parallel along curves. This method was precisely formulated by Tullio Levi-Civita . Today it is mostly referred to as parallel transport but also as parallel displacement.

Affine geometry

In axiomatically constructed affine geometry ( synthetic geometry ), a collineation is called a translation if the following two conditions are met: ${\displaystyle {\mathcal {\alpha }}}$

• Straight lines are mapped onto parallel straight lines.
• If any point is changed at all, the figure has no fixed point.

T ₁ :     ${\displaystyle \forall g\in {\mathcal {G}}\colon \;\alpha (g)\parallel g}$

T ₂ :     ${\displaystyle \forall P\in {\mathcal {P}}\colon \;\alpha \neq \mathrm {id} \,\Rightarrow \,\alpha (P)\neq P}$

( is the set of all points, the set of all lines, see incidence ). These translations can be used, for example, in an affine translation plane as position vectors of the points. ${\displaystyle {\mathcal {P}}}$ ${\displaystyle {\mathcal {G}}}$

Here, too, translation is always an affinity in the sense of synthetic geometry. The continuation of a translation in the projective closure of the affine space is a projective perspective and therefore a projectivity .

See also

When defining the term parallel translation or translation , different emphases are set in different areas of geometry and linear algebra, whereby the generalized definition is valid everywhere. Please refer

• on the concept of parallel displacement in the elementary geometry of the plane of the drawing : congruence mapping .
• on the concept of parallel displacement in three-dimensional visual space: movement (mathematics) .
• on the concept of translation in synthetic geometry : Affine translation level .
• on linear motion in physics: translation (physics)

literature

Parallel shift in linear algebra and planar and spatial geometry:

• Uwe Storch, Hartmut Wiebe: Textbook of Mathematics, Volume II: Linear Algebra . BI-Wissenschafts-Verlag, 1990, ISBN 3-411-14101-8

Translation in synthetic geometry:

• Wendelin Degen and Lothar Profke: Fundamentals of affine and Euclidean geometry , Teubner, Stuttgart, 1976, ISBN 3-519-02751-8
• Günter Pickert : Level incidence geometry. 2nd edition, Frankfurt am Main 1968

Web links

Commons : Parallel Shift  - collection of images, videos and audio files

• Displacement and ribbon ornaments - materials for independent work for students

Individual evidence

1. ↑ Sword (1976)