Incidence Geometry

In mathematics, incidence geometry is understood to be a geometry that is characterized by a so-called incidence relation . In clear terms, the incidence relation explains which points are contained in a certain straight line or how and whether straight lines intersect.

Incidence geometry offers an axiomatic approach to geometry and places the definitions that are otherwise very clear (because they arise from observing nature) on an abstract level by initially only using elementary terms from set theory .

General geometry of incidence

definition

An incidence structure is a triple consisting of a set of points, a set of blocks (straight lines) and an incidence relation , i.e. a subset . The incidence structure is called incidence geometry if any two points with exactly one straight line incline. ${\displaystyle (P,B,I)}$ ${\displaystyle P}$ ${\displaystyle B}$ ${\displaystyle I}$ ${\displaystyle I\subset P\times B}$

Examples of incidence geometries

• Space becomes an incidence geometry as follows: the set of points is , the set is the set of all affine lines in . Incise two elements when is, ie . ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle P=\mathbb {R} ^{3}}$ ${\displaystyle B}$ ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle x\in P,g\in B}$ ${\displaystyle x\in g}$ ${\displaystyle (x,g)\in I\Leftrightarrow x\in g}$

Subspaces and dimensions in the incidence geometry

A set is called a linear set if for every straight line that cuts with two points from , every additional point that cuts with lies in. A linear set of together with its associated straight lines forms an incidence geometry, which is referred to as a subspace or sub geometry of . ${\displaystyle M\subset P}$ ${\displaystyle g}$ ${\displaystyle M}$ ${\displaystyle g}$ ${\displaystyle M}$ ${\displaystyle P}$ ${\displaystyle (P,B,I)}$

This defines the concept of the linear envelope in a very similar way to that in linear algebra : The linear envelope of a set is the intersection of all linear sets that contain. is therefore the smallest linear amount that contains. ${\displaystyle \langle M\rangle }$ ${\displaystyle M\subset P}$ ${\displaystyle M}$ ${\displaystyle \langle M\rangle }$ ${\displaystyle M}$

A set is called the base of the set if and when there is no smaller set that has the same property. The dimension of a room can then be defined in such a way that it is 1 smaller than the thickness of a base. ${\displaystyle M\subset P}$ ${\displaystyle P}$ ${\displaystyle \langle M\rangle =P}$

Differences to Euclidean Geometry

Example of an incidence geometry

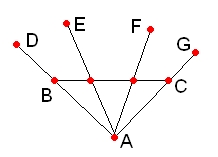
• The concept of dimension is far less clear in incidence geometry than in Euclidean geometry . If you look at the geometry in the right figure, which consists of 9 points (only the straight lines that contain more than 2 points are shown), the points form a basis, ie the space has dimension 2. The points, however, together form one Linear quantity. Together with their associated straight lines, they therefore form a subspace. But now the set is a basis of this subspace, which therefore has dimension 3. I.e. it is possible that a room has a smaller dimension than one of its sub-rooms. ${\displaystyle A,B,C}$ ${\displaystyle D,E,F,G}$ ${\displaystyle \{D,E,F,G\}}$

Special incidence geometries

Projective geometry

A projective geometry is an incidence geometry that satisfies the Veblen-Young axiom : If , are the lines through or , and there is a point with which both and incise, then there is also a point with which both and incise . ${\displaystyle (P,B,I)}$ ${\displaystyle A,B,C,D\in P}$ ${\displaystyle g_{AB},g_{CD}}$ ${\displaystyle A,B}$ ${\displaystyle C,D}$ ${\displaystyle g_{AB}}$ ${\displaystyle g_{CD}}$ ${\displaystyle g_{AD}}$ ${\displaystyle g_{CB}}$

Another axiom can be added to this axiom , which requires that every straight line incurs at least 3 points and that there are at least 2 straight lines. A projective geometry which does not fulfill this axiom is called degenerate .

The Veblen-Young-Axiom states that two straight lines that run in a common plane always have an intersection point (ie there are no parallel straight lines).

Affine geometry

An affine geometry is an incidence geometry with the following properties: ${\displaystyle (P,B,I)}$

• The geometry has a parallelism, that is, equivalence relation which at a fixed chosen point each line a unique straight line , so that allocates and incise, ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle P}$ ${\displaystyle h}$
• If parallel straight lines are a point that neither with nor with incised and are straight lines which incise with and which intersect, then the straight lines intersect and , if and intersect (trapezoid axiom). ${\displaystyle g,g'}$ ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle g'}$ ${\displaystyle h,h'}$ ${\displaystyle P}$ ${\displaystyle g}$ ${\displaystyle h'}$ ${\displaystyle g'}$ ${\displaystyle h}$ ${\displaystyle g'}$

Again one can add the axiom that there are two lines and that every line intersects with at least 3 points. An affine geometry which does not fulfill this axiom is also called degenerate .

In clear terms, the trapezoid axiom says that two parallel straight lines always run in a common plane.

If parallelism is understood as an equivalence relation, as in this definition, then it is particularly true that a straight line is parallel to itself, otherwise the relation would not be reflexive.

literature

• F. Buekenhout: Handbook of Incidence Geometry. North Holland 1995. ISBN 978-0-444-88355-1
• Albrecht Beutelspacher , Ute Rosenbaum: Projective geometry. From the basics to the applications . Vieweg + Teubner, Braunschweig et al. 1992, ISBN 3-528-07241-5 (2nd, reviewed and expanded edition. Vieweg, Wiesbaden et al. 2004, ISBN 3-528-17241-X )
• Johannes Ueberberg: Foundations of Incidence Geometry . Springer Monographs in Mathematics, Springer, 2011, doi : 10.1007 / 978-3-642-20972-7 , ISBN 978-3-642-26960-8 .

Web links

• G. Eric Moorhouse: Incidence Geometry . Script, University of Wyoming, August 2007
• Incidence geometry (definition) ( Memento from April 26, 2009 in the Internet Archive )
• Incidence Geometry at PlanetMath