Set theory
The set theory is a fundamental branch of mathematics that deals with the study of quantity , ie summaries of objects employed. All of mathematics as it is usually taught today is formulated in the language of set theory and is based on the axioms of set theory . Most mathematical objects that are dealt with in sub-areas such as algebra , analysis , geometry , stochastics or topology , to name just a few, can be defined as sets. Measured against this, set theory is a very young science; Only after overcoming the fundamental crisis in mathematics in the early 20th century was set theory able to take its current, central and fundamental place in mathematics.
history
19th century
Set theory was founded by Georg Cantor between 1874 and 1897. Instead of the term quantity , he initially used words such as "epitome" or "manifold"; He spoke of sets and set theory only later. In 1895 he formulated the following definition of quantities:
"By a 'set' we mean any combination M of certain well-differentiated objects m of our perception or our thinking (which are called the 'elements' of M) into a whole."
Cantor classified the sets, especially the infinite ones, according to their thickness . For finite sets this is the number of their elements. He called two sets of equal power if they can be mapped bijectively to one another, that is, if there is a one-to-one relationship between their elements. The uniformity defined in this way is an equivalence relation and the cardinality or cardinal number of a set M is, according to Cantor, the equivalence class of the sets of equal power to M. He was probably the first to observe that there are various infinite powers. The set of natural numbers and all sets of equal power to them are called countable according to Cantor , all other infinite sets are called uncountable .
- Important results from Cantor
- The sets of natural , rational ( Cantor's first diagonal argument ) and algebraic numbers can be counted and are therefore equal.
- The set of real numbers has greater power than that of natural numbers, so it is not countable ( Cantor's second diagonal argument ).
- The set of all subsets of a set M (their power set ) always has greater power than M , this is also known as Cantor's theorem.
- Of every two sets, at least one is equal to a subset of the other. This is proven with the help of the well-order discussed in detail by Cantor .
- There are many powers that cannot be counted.
Cantor named the continuum problem : “Is there a power between that of the set of natural numbers and that of the set of real numbers?” He tried to solve it himself, but was unsuccessful. It later turned out that the question cannot be decided in principle.
In addition to Cantor, Richard Dedekind was also an important pioneer in set theory. He spoke of systems instead of sets and in 1872 he developed a set-theoretical construction of real numbers and in 1888 a verbal set-theoretical axiomatization of natural numbers. He was the first to formulate the axiom of extensionality in set theory.
Giuseppe Peano , who referred to sets as classes , created the first formal class logic calculus in 1889 as the basis for his arithmetic with the Peano axioms , which he first formulated in a precise set-theoretical language. He thus developed the basis for today's formula language of set theory and introduced many symbols in use today, especially the element sign , which is verbalized as "is an element of". It is the small initial letter ε ( epsilon ) of the word ἐστί ( Greek "is").
A little later , Gottlob Frege attempted another set-theoretic justification of arithmetic in his calculus of 1893. In this calculus, Bertrand Russell discovered in 1902 a contradiction which became known as Russell's antinomy . This contradiction and other contradictions arise due to an unrestricted set formation, which is why the early form of set theory was later referred to as naive set theory . Cantor's definition of sets does not intend such a naive set theory, as his proof of the universal class as a non-set by Cantor's second antinomy shows.
Cantor's set theory was hardly recognized by his contemporaries and was by no means viewed as a revolutionary advance, but met with rejection from some mathematicians, such as Leopold Kronecker . It was even more discredited when antinomies became known, so that Henri Poincaré , for example, scoffed: "Logic is no longer sterile - it now generates contradictions."
20th century
Cantor's ideas became more and more popular in the 20th century; At the same time, within the developing mathematical logic, an axiomatization of set theory took place , by means of which previous contradictions could be overcome.
In 1903/1908 Bertrand Russell developed his type theory , in which sets always have a higher type than their elements, so that problematic set formations would be impossible. He showed the first way out of the contradictions and in the Principia Mathematica from 1910–1913 also showed a piece of the efficiency of applied type theory. Ultimately, however, it turned out to be inadequate for Cantor's set theory and, because of its complexity, could not prevail.
On the other hand, the axiomatic set theory developed by Ernst Zermelo in 1907, which he created specifically for the consistent justification of the set theory of Cantor and Dedekind, was more handy and successful . Abraham Fraenkel noted in 1921 that this also required his substitution axiom . Zermelo added it to his Zermelo-Fraenkel system from 1930 , which he called the ZF system for short. He also conceived it for primordial elements that are not sets, but can be considered as set elements and take Cantor's “objects of our perception” into account. Today's Zermelo-Fraenkel set theory , on the other hand, is, according to Fraenkel, a pure set theory whose objects are exclusively sets.
Instead of a consistent axiomatization, however, many mathematicians rely on a pragmatic set theory that avoided problem sets, such as the set theories of Felix Hausdorff from 1914 or Erich Kamke from 1928. Gradually, more and more mathematicians became aware that the Set theory is an indispensable basis for structuring mathematics. The ZF system has proven itself in practice, which is why it is now recognized by the majority of mathematicians as the basis of modern mathematics; no more contradictions could be derived from the ZF system. The consistency could only be proven for set theory with finite sets, but not for the complete ZF system, which contains Cantor's set theory with infinite sets; According to Gödel's incompleteness theorem of 1931, such a proof of consistency is in principle not possible. Godel's discoveries only put a limit on Hilbert's program of placing mathematics and set theory on a demonstrably consistent axiomatic basis, but in no way hindered the success of set theory, so that a fundamental crisis in mathematics , of which supporters of intuitionism spoke, actually became reality nothing was felt.
The final recognition of ZF set theory in practice, however, dragged on for a long time. The mathematicians group with the pseudonym Nicolas Bourbaki contributed significantly to this recognition; she wanted to represent mathematics in a uniform new way on the basis of set theory and implemented this successfully in central areas of mathematics from 1939 onwards. In the 1960s it became common knowledge that ZF set theory is suitable as a basis for mathematics. There was even a temporary period when set theory was discussed in elementary school .
Parallel to the success story of set theory, however, the discussion of set axioms in the professional world remained topical. There were also alternative axiomatic set theories , around 1937 the set theory of Willard Van Orman Quine from his New Foundations (NF), which was not based on Cantor or Zermelo-Fraenkel, but on type theory , and in 1940 the Neumann-Bernays-Gödel set theory , the ZF generalized to classes , or in 1955 the Ackermann set theory , which was based on Cantor's set definition.
Definitions
In pure set theory, the element predicate (i.e. is an element of ) is the only necessary basic relation. All set theoretic concepts and statements are defined from it with logical operators of predicate logic .
- Bulleted notation
- The set, which consists of the elements to , contains the element if and only if it matches one of the . Formally:
- For example, the statement is
- equivalent to the statement
- Descriptive notation
- The set to which the predicate applies contains an element if and only if the predicate applies to. Formally:
- There is also a restricted variant of this unrestricted description:
- Often there is also the short form
- before, whereby a functional term is meant.
- According to the definition of the equality of two sets, the statement
- now in the logical expression
- dissolve.
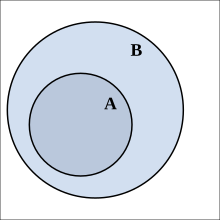
- Subset
- A set is called a subset of a set if every element of is also an element of . Formally:
- Empty set
- The set that does not contain an element is called the empty set. It is also referred to as or .
- Write shorter for the negation .
- Intersection
- A non-empty set of sets is given. The intersection (also average set ) of is the set of objects that are contained in each element of - that is in turn a set. Formally:
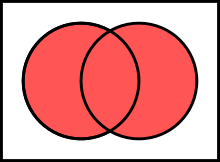
- Union set
- This is the dual term for the intersection : The union of a (not necessarily non-empty) set of sets is the set of objects that are contained in at least one element of . Formally:
- Equality of sets
- Two sets are called the same if they contain the same elements.
- This definition describes the extensionality and thus the fundamental property of sets. Formally:
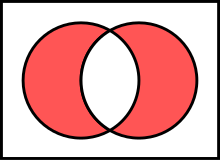
- Difference and complement
- The difference is usually only defined for two sets: The difference set (also remainder ) of and (colloquially also A without B , see Fig.) Is the set of elements that are contained in , but not in . Formally:
- The difference is also called complement of B with respect to A . If the set A is assumed as the basic set and B is a subset of A , one simply speaks of the complement of the set B and writes e.g. B .:
- Symmetrical difference
- Sometimes the "symmetrical difference" is still required:
- Power set
- The power of a set is the set of all subsets of .
- The power set of a set always contains the empty set and the set itself. Thus , is a one-element set.
- Orderly couple
The concept of the ordered pair is also traced back to. According to Kuratowski , this happens in two steps:
- Set of two:
- Ordered pair:
- Cartesian product
- The product set or the Cartesian product , in older terminology also compound set or product of the second kind, should also be defined here as a link between two sets:
- The product set of and is the set of all ordered pairs whose first element is off and whose second element is off.
- Relations and functions
- A relation between and is a subset .
- A function from to , in signs , is a relation with
- (i.e. for each there is at least one function value)
- (i.e. for each there is at most one function value).
- For one writes more suggestively . This means that these terms can also be traced back to the relationship. This allows further terms such as equivalence relation , injective function , surjective function , bijective function and much more to be defined.
- Quotient set
- If there is an equivalence relation , the equivalence class of an element can first be defined:
- The set of all equivalence classes is called the quotient set:
- Says the equivalence relation z. For example, if two students go to the same class, then the equivalence class of a student is his school class and the quotient set is the number of school classes in the school.
- Natural numbers
According to John von Neumann , natural numbers can be defined in set theory as follows:
This should make it clear how one can use the above definitions to reduce all other mathematical concepts to the concept of sets.
- Cardinal number and cardinal number
- With the terms of the bijective function and the equivalence relation, the aforementioned power of a set can now also be defined. The cardinality or cardinality of a set is denoted by (sometimes also # ). A set is called finite, if it is equal to a natural number, then the number of elements is of . The term cardinal number is thus a generalization of the number of elements of a (finite) set. Taking into account the arithmetic of the cardinal numbers , the power of the power set of , even with infinite sets, is denoted by.
Regularities
The set is partially ordered with respect to the relation , because the following applies to all :
- Reflexivity :
- Antisymmetry : off and follows
- Transitivity : out and follows
The set operations cut and union are commutative, associative and distributive to one another:
-
Associative law :
- and
-
Commutative law :
- and
-
Distributive law :
- and
-
De Morgan's Laws :
- and
- Law of absorption:
- and
The following principles apply to the difference:
- Associative Laws:
- and
- Distributive Laws:
- and
- and
- and
The following principles apply to the symmetrical difference:
- Associative law:
- Commutative law:
- Distributive law:
See also
literature
- Felix Hausdorff : Fundamentals of set theory . Chelsea Publ. Co., New York 1914/1949/1965, ISBN 978-3-540-42224-2 .
- Adolf Fraenkel : Introduction to set theory . Springer, Berlin / Heidelberg / New York, NY 1928. Reprint: Martin Sendet oHG, Walluf 1972, ISBN 3-500-24960-4 .
- Paul R. Halmos : Naive set theory . Vandenhoeck & Ruprecht, Göttingen 1968, ISBN 3-525-40527-8 .
- Erich Kamke : set theory. 7th edition. Walter de Gruyter & Co., Berlin 1971, ISBN 3-11-003911-7 .
- Kenneth Kunen : Set Theory: An Introduction to Independence Proofs. North-Holland, 1980, ISBN 0-444-85401-0 .
- Arnold Oberschelp : General set theory . BI-Wissenschaft, Mannheim / Leipzig / Vienna / Zurich 1994, ISBN 3-411-17271-1 .
- Oliver Deiser: Introduction to set theory . Georg Cantor's set theory and its axiomatization by Ernst Zermelo. 3. Edition. Springer, Berlin / Heidelberg 2010, ISBN 978-3-642-01444-4 .
- André Joyal, Ieke Moerdijk: Algebraic Set Theory . Cambridge University Press, 1995, ISBN 0-521-55830-1 .
- Heinz-Dieter Ebbinghaus : Introduction to set theory . Spectrum Academic Publishing House, Heidelberg / Berlin 2003, ISBN 3-8274-1411-3 .
Web links
- Christian Spannagel : Set theory . Lecture series, 2010.
Individual evidence
- ^ Georg Cantor: Contributions to the foundation of the transfinite set theory. In: Mathematische Annalen 46 (1895), p. 481. Online version . See text passage with the set definition by Georg Cantor.png for an image of the corresponding text passage.
- ^ Richard Dedekind: Continuity and Irrational Numbers. Braunschweig 1872.
- ↑ Richard Dedekind: What are and what are the numbers? Brunswick 1888.
- ^ Giuseppe Peano: Arithmetices Principia nova methodo exposita. Turin 1889.
- ↑ Ingmar Lehmann , Wolfgang Schulz: "Quantities - Relations - Functions" (3rd edition, 2007), ISBN 978-3-8351-0162-3 .
- ^ Letter from Cantor to Dedekind of August 31, 1899, in: Georg Cantor: Collected treatises of mathematical and philosophical content . ed. E. Zermelo, Berlin 1932, p. 448.


















































![{\ displaystyle [a]: = \ {x \ in M \ mid a \ sim x \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eef06ff61302c1c07d975ca877f74d4f30f109e9)
![{\ displaystyle M / {\ sim}: = \ {[a] \ mid a \ in M \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9135e272fcd90a89abd4a4a95ccbe3add7d32e8a)

































