Transitive relation

This article or the following section is not adequately provided with supporting documents ( e.g. individual evidence ). Information without sufficient evidence could be removed soon. Please help Wikipedia by researching the information and including good evidence.

Transitive two and a non-transitive relation (bottom right) as directed graphs shown

A transitive relation is in mathematics a double-digit relation to a quantity that for three elements that has the property , , the amount of and always follows. Examples of transitive relations are the direct and the less-relations to the real numbers , because for three real numbers , and with and applies always , and out and followed . ${\displaystyle R}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle xRy}$ ${\displaystyle yRz}$ ${\displaystyle xRz}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle x=y}$ ${\displaystyle y=z}$ ${\displaystyle x=z}$ ${\displaystyle x<y}$ ${\displaystyle y<z}$ ${\displaystyle x<z}$

A non-transitive relation is called intransitive (not to be confused with negative transitivity ). Transitivity is one of the prerequisites for an equivalence relation or an order relation .

Formal definition

If there is a set and a two-digit relation , then is said to be transitive if (using the infix notation ): ${\displaystyle M}$ ${\displaystyle R\subseteq M\times M}$ ${\displaystyle M}$ ${\displaystyle R}$

${\displaystyle \forall x,y,z\in M:xRy\land yRz\Rightarrow xRz.}$

Representation as a directed graph

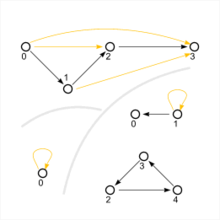
Any relation on a set can be interpreted as a directed graph (see example above). The nodes of the graph are the elements of . A directed edge (an arrow ) is drawn from node to node if and only if applies. ${\displaystyle R}$ ${\displaystyle M}$ ${\displaystyle M}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a\longrightarrow b}$ ${\displaystyle aRb}$

The transitivity of can now be characterized in the graph as follows: Whenever two arrows follow one another ( ), there is also an arrow that directly connects the start and end nodes ( ) (also in the Hasse diagram ). ${\displaystyle R}$ ${\displaystyle a\longrightarrow b\longrightarrow c}$ ${\displaystyle a\longrightarrow c}$

properties

• The transitivity of a relation also allows conclusions to be drawn across several steps (as can easily be shown by complete induction ): ${\displaystyle R}$

  ${\displaystyle a\,R\,b_{1}\,R\,b_{2}\,R\,\dots \,R\,b_{n}\,R\,c\implies a\,R\,c}$

• With the help of the chaining of relations, transitivity can also be characterized by the following condition: ${\displaystyle \circ }$

  ${\displaystyle R\circ R\subseteq R}$

• If the relation is transitive, then this also applies to the converse relation . Examples: the relation is too converse, the relation is too converse . ${\displaystyle R}$ ${\displaystyle R^{-1}}$ ${\displaystyle \leq }$ ${\displaystyle \geq }$ ${\displaystyle <\ }$ ${\displaystyle >\ }$
• If the relations and are transitive, then this also applies to their intersection . This statement can be generalized from two relations to the intersection of any family of transitive relations. ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle R\cap S}$ ${\displaystyle \cap _{i\in I}R_{i}}$
• For every relation there is a smallest transitive relation that contains, the so-called transitive envelope of . Example: let the predecessor relation be on the set of natural numbers, so it applies . The relation itself is not transitive. The smaller relation results as the transitive envelope of . ${\displaystyle R}$ ${\displaystyle S}$ ${\displaystyle R}$ ${\displaystyle R}$
  ${\displaystyle R}$ ${\displaystyle a\,R\,b:\Longleftrightarrow a=b-1}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle <\ }$

Examples

Order of real numbers

From a> b and b> c follows a> c.

The smaller relation on the real numbers is transitive, because it follows from and . It is also a strict total order . ${\displaystyle <\ }$ ${\displaystyle x<y}$ ${\displaystyle y<z}$ ${\displaystyle x<z}$

Likewise, the relations , and are transitive. ${\displaystyle >\ }$ ${\displaystyle \leq \ }$ ${\displaystyle \geq \ }$

Equality of real numbers

Ordinary equality on real numbers is transitive, because it follows from and . It is also an equivalence relation . ${\displaystyle =\ }$ ${\displaystyle x=y}$ ${\displaystyle y=z}$ ${\displaystyle x=z}$

The inequality relation on the real numbers, however, is not transitive: and , but of course does not hold. ${\displaystyle \neq }$ ${\displaystyle 3\neq 5}$ ${\displaystyle 5\neq 3}$ ${\displaystyle 3\neq 3}$

Divisibility of the whole numbers

The divisibility relation for integers is transitive, because it follows from and . It is also a quasi-order . If you restrict to the set of natural numbers , you get a partial order . ${\displaystyle |}$ ${\displaystyle a|b}$ ${\displaystyle b|c}$ ${\displaystyle a|c}$

Not, for example, is transitive the coprimality . So and are coprime, just as and , but have and the common factor . ${\displaystyle 12}$ ${\displaystyle 5}$ ${\displaystyle 5}$ ${\displaystyle 9}$ ${\displaystyle 12}$ ${\displaystyle 9}$ ${\displaystyle 3}$

Subset

The subset relationship between sets is transitive, because it follows from and . In addition, is a partial order. ${\displaystyle \subseteq }$ ${\displaystyle A\subseteq B}$ ${\displaystyle B\subseteq C}$ ${\displaystyle A\subseteq C}$ ${\displaystyle \subseteq }$

For example, the disjointness of sets is not transitive . The sets and are disjoint, as are and , but not and (since they have the element 1 in common). ${\displaystyle \lbrace 1,2\rbrace }$ ${\displaystyle \lbrace 3\rbrace }$ ${\displaystyle \lbrace 3\rbrace }$ ${\displaystyle \lbrace 1,4\rbrace }$ ${\displaystyle \lbrace 1,2\rbrace }$ ${\displaystyle \lbrace 1,4\rbrace }$

Parallel straight lines

In the geometry that is parallelism of straight transitive: If both the straight and parallel and the straight lines and then also and in parallel. In addition, the parallelism is an equivalence relation. ${\displaystyle g_{1}}$ ${\displaystyle g_{2}}$ ${\displaystyle g_{2}}$ ${\displaystyle g_{3}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{3}}$

Implication in logic

In logic , transitivity applies to the implication , although this is also known as modus barbara in predicate logic :

From and follows (compare also: rule of intersection ). ${\displaystyle A\Rightarrow B}$ ${\displaystyle B\Rightarrow C}$ ${\displaystyle A\Rightarrow C}$

The implication defines a quasi-order on the formulas of the logic under consideration.

See also

• Transitive envelope
• Negative transitivity

Web links

• Transitivity . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).