Intransitive relation

An intransitive relation is in mathematics a double-digit relation to a quantity that it has the property at least three elements , , are from this amount for and apply, but not . A relation is therefore intransitive if it is not transitive . Originally, intransitive relations were examined by the Marquis de Condorcet in connection with elections (see also Condorcet paradox ). ${\displaystyle R}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle xRy}$ ${\displaystyle yRz}$ ${\displaystyle xRz}$

Formal definition

If there is a set and a two-digit relation , then it is called intransitive if: ${\displaystyle M}$ ${\displaystyle R\subseteq M\times M}$ ${\displaystyle M}$ ${\displaystyle R}$

${\displaystyle \exists x,y,z\in M:xRy\land yRz\land \neg xRz.}$

Examples

The figures of scissors, stone, paper

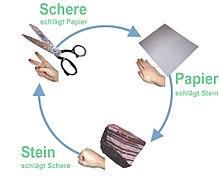
A clear example of an intransitive preference relation is the game of scissors, stone, paper . The choice of stone against scissors, scissors against paper and paper against stone wins. If the relation were transitive, then “stone wins against scissors” and “scissors wins against paper” would have to follow: “stone wins against paper”, which contradicts the rules of the game. For this reason the relation can no longer be transitive, it is intransitive.

Another example of an intransitive relation are intransitive cubes .

literature

• Patrick Suppes : Introduction to Logic , Dover Pubn Inc, 1999, ISBN 0-486-40687-3