Relation (mathematics)
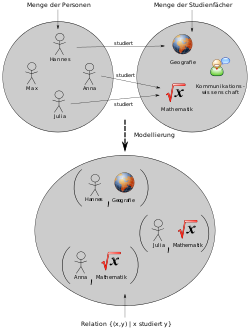
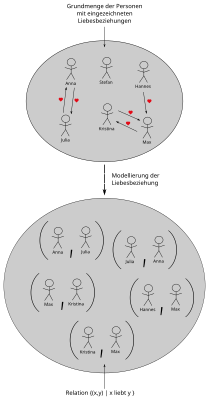
A relation ( Latin relatio "relationship", "relationship") is generally a relationship that can exist between things. Relations in the sense of mathematics are exclusively those relationships for which it is always clear whether they exist or not; Objects cannot be related to one another “to a certain extent”. This enables a simple set- theoretical definition of the term: A relation is a set of tuples . Things that are related to one another form tuples that are elements of .
Unless expressly stated otherwise, a relation is generally understood to be a two-digit or binary relation . In such a relationship, then two elements form and an ordered pair originate and from different base levels and is the name of the relation heterogeneous or "relation between the amounts and ." If the basic quantities match ( ), then that means the relation homogeneously or "Relation in or on the crowd . "
Important special cases , for example equivalence relations and order relations , are relations on a set.
Today, some authors consider the term relation not necessarily as to amounts limited to but let each consisting of ordered pairs class are considered relation.
Definitions
Double-digit relation
A two-digit relation (also called binary relation ) between two sets and is a subset of the Cartesian product
- .
The set is referred to as the source set (English: set of departure ) of the relation , the set as the target set (English: set of destination ).
Sometimes, however, this definition is not precise enough and referring the source and target quantity in the definition of a, above is then subset of the graph (more rarely Count ) called the relation. A two-digit relation is then defined as a triple
- with .
Knowing the source and target set is particularly important when considering functions as special (so-called functional) relations.
The archetype, argument or definition or pre-range of a given two-digit relation is understood as the smallest possible pre-range to the graph , the elements of which all appear in the ordered pairs of actually on the left side, in signs
- .
The set of values, values or image or after- area in this sense denotes the smallest after-area for a given , whose elements all appear in the pairs from on the right-hand side, in characters
- .
Sometimes the term field (or node set ) is used for the union set , in characters
- .
In addition, the following designations can be found:
- Domain (English domain ) either for the (in principle arbitrarily large) source set or for the original image set (defined by the graph) (domain of definition),
- Co-domain (English codomain , range ) either for the target set or for the image set,
- Set of nodes ( ) for the field of a relation.
If two relations agree in their graphs, one also says that they are essentially the same.
Example: Every relation is essentially the same with and with the homogeneous relation .
n -digit relation
More generally, a -digit relation is a subset of the Cartesian product of sets
- with .
Here denotes the finite sequence of the sets, and the Cartesian product.
The more detailed definition can also be generalized to -place relations and one then obtains the -tuple
- with .
The amounts of hot carriers amounts of relation with the minimum support amounts to the graph , namely
- .
The field of a -digit relation is given by
- .
Substantial equality is defined in the same way as for two-digit relations by the correspondence of the graphs, in particular every -digit relation is essentially the same with and with the homogeneous relation .
- One-digit and zero-digit relation
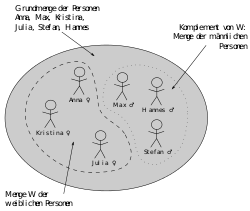
A one- digit relation on a set is therefore simply a subset , in the detailed definition with .
The zero-digit relations are therefore the subsets of the empty Cartesian product or , that is, and , detailed and .
Relations between or on real classes
Often the carrier areas of a relation are not sets, but real classes , one then speaks of class relations . Occasionally one can avoid the set-theoretic problems that result from this by only looking at the graph of the corresponding relation. The (minimum) carrier quantities ( in the two-digit case definition and value set ) are actually quantities, but it is not necessary to specify the source quantity, target quantity, ... ( ) from the outset if the relations are essentially the same. Not always it is possible, for example for the equivalence relation of equal thickness , see also: cardinal numbers §Definition . Essentially equality of relations is another example.
A two-digit class relation with source class and target class is called small predecessor if the class of the predecessor (archetype fiber of , see below) is a set (i.e. not a real class) for all . The relation is called English right-narrow (German about successor small ), if for all the class of the successor (image fiber of ) is a lot. In the case of right uniqueness (partial mappings, mappings, see below), a class relation is always small, since there is one image value for every archetype (exactly or at most), i.e. the class of the successors is a set of ones (or the empty set ). Every injective class mapping is both small and predecessor small. The inclusion relation is small for each class , since they can not be real classes, but are sets and are therefore also a set. The terms predecessor and successor themselves are usually used in the context of order relations, see order relation §Predecessor and successor .
Explanations and notations
The Cartesian product of two sets and is the set of all ordered pairs of and where any element from the set and one from represents. In the ordered pair, the order is important; H. differs from in contrast to the disordered pair, which is identical to For , is also written to make it clear that there is that relationship between the objects (as in ). The empty set as a subset of the Cartesian set product understood as a relation is called the zero relation , the full product is called the all relation (also known as universal relation ) (also referred to as ).
Relations and functions
- A function is a special one, namely a left-total and right-unique (two-digit) relation, see below for details .
- A multifunction is a left total relation .
- A partial function is a right-unambiguous relation (generally not a left total) .
In all cases (or if the detailed definition is used).
The following applies to functions and multi-functions:
- In the more detailed definition , because it is clearly determined by (left total), it can also be omitted and taken more simply .
The following applies to functions and partial functions:
- For or is also written (English: maplet ), or .
In general:
- The zero-place relations (as zero-place zero relation) and (as zero-place full relation) have as characteristic functions the Boolean or logical constants and , as always for zero relation and all relation.
- The case of single-digit relations is trivial.
- A relation (or ) corresponds in a unique way to a truth function . This function is also known as the indicator function or characteristic function of the subset (or ), where can be replaced by .
- A -digit relation (or ) corresponds to the characteristic function
The following applies:
- .
- .
- .
- .
- A relation can also be understood as a mapping of into the power set of , one then often speaks of a correspondence , and for of a transition relation .
Chaining of relations
The forward chaining of two two-digit relations is defined as follows:
Chaining in the reverse order is called backward chaining :
- .
Some authors (W. v. O. Quine) use the notation for this as an alternative .
The sequence for backward chaining is the same as for chaining functions (which can be seen as special relations).
The concatenation of two-digit relations is also known as a relative product . In the concatenation, the simplest relation that contained in each Cartesian product can empty relation ( empty set ) occur, namely, when and disjoint are in symbols .
Example: The relation “being sister-in-law of” is the union
- of the relative product of the relation “being brother of” and the relation “being wife of” and
- the relative product of the relation “being spouse of” and the relation “being sister of”.
Inverse relation
The inverse relation (also called converse relation, converse or inverse relation) is defined as for a two-digit relation
- .
Occasionally, the term transposed relation is also used for this , in characters .
- Example 1: The inverse relation of the relation "is descendant of" is the relation "is ancestor of".
- Example 2: The inverse relation of the relation “is less than” is the relation “is greater than”.
- Example 3: The reverse relation of the relation “delivers to” is the relation “is supplied by”.
The generalization of the inverse relation (converse) to -sign relations is the permutation of the coordinates of the -tuples it contains , special
- the interchanges of only 2 coordinates ( transpositions ) and
- the reversal of the order ( mirroring ),
both examples of ( cyclic ) self-inverse permutations .
Let be a permutation (i.e. a bijective mapping of to itself) and be a --place relation, then the relation resulting after applying the permutation is (one understands as a family ). In the case of mirroring
is .
Image and archetype
In a two-digit relation , the image of a set or class is the set or class
- .
The archetype of a set or class is the set or class
- .
Occasionally the designation (sic!) Is also found for this , often also with square brackets as noted. In correspondence of a for the image fiber of an amount (Singleton) , the notation is what partially also uses the bracket notation in use, i. H. ; in the case of symmetrical relations, d. H. (possibly partial) equivalence or compatibility relations is the notation and speaks of equivalence or compatibility or tolerance classes.
Restriction
Relations can be restricted in various ways to subsets of the carrier sets, for more information see Restricting a relation .
Complementary relation
For two-digit relations with a fixed pre- and post-range the complementary relation is given by
- ,
analogous for -digit relations for fixed support areas . For example, on the real numbers , the complementary relation to is .
If the complex notation is used, then is
- ,
where there are no longer any external additions, but components of the relation; analogous for -digit relations in this notation.
As for all sets, the complement is also involutive for relations:
- .
Homogeneous relations
If , then, the relation is called homogeneous. Some authors define a general relation already as a homogeneous relation, as a general relation can always be considered as a homogeneous limitation: .
Special homogeneous relations and operations on homogeneous relations
A special homogeneous relation in a set is the equality or identity relation or diagonal
Alternative notations for the diagonal are or ; if already known, it is simply referred to as , or .
Another special homogeneous relation is the all relation or universal relation
- (also referred to as Nabla as ).
If it is already known, the index is omitted here as in the case of the identity relation.
The all relation plays a role in graph theory (see below). An example of use is the following sentence:
- Is a directed graph with a lot of corners and a (associated) relationship of edges, it is then exactly coherent (strong) when the reflexive transitive closure of the Universal relation.
The formation of the inverse relation (converse relation) of a homogeneous two-digit relation again provides a homogeneous two-digit relation (closeness), twice execution again results in the starting relation (involutivity). The connection of any (also non-homogeneous) relation with the relation to which it is converted is symmetrical and reflexive, i.e. an equivalence relation, but in general not the same as the identity relation.
In the case of a homogeneous relation , the concatenation is also a homogeneous relation, so that the homogeneous relations form a monoid with the multiplicative relation and the neutral element . Thus, and to general powers to be defined, which is. is therefore also called one relation on the set .
In extension of the notation instead of for the inverse relation, one denotes its powers with negative exponents:
- .
This means that any whole numbers are allowed as exponents.
In addition, every monoid has homogeneous relations with the empty relation ( zero relation )
another absorbent element .
The relations arise through the union of the different powers
- and .
Algebraic structures
Taken together, the two-digit relations on a set form a relation algebra
Using the notations .
Together with the restrictions, the homogeneous relations form a ( heterogeneous ) Peirce algebra .
Homogeneous multi-digit relations
Homogeneous multi-digit relations are (with their graph) subsets of . For solid the all relation (also ) and the identity relation (diagonal) (also ) are given by
- .
The application of permutations to their -tuples, described as a generalization of the formation of conversions, is of particular importance here, since in this way one always remains within the subsets of (closeness). M. a. W. These operations are bijective mappings in . Other terms known from two-digit relations, such as reflexivity and symmetry, etc., can be canonically (naturally) extended to any multi-digit relations.
Graph theory and generalizations
Graph theory describes sets with a relation to them together with certain generalizations under a common generic term, the graph . The cases considered in graph theory are (unless otherwise stated) usually finite.
1. A relational structure consisting of a set together with a relation on it is called a directed (also oriented ) graph . is called the set of nodes of the graph, its elements are called nodes . is called a subset of the set of edges , its elements (ordered pairs of ) are called directed (i.e., oriented ) edges .
2. Symmetric graphs , i.e. H. Sets with a symmetrical relation are equivalent to an undirected graph , whose edge set consists of (undirected) edges, namely the (disordered) sets with (here equivalent to ).
3. Further generalizations concern so-called directed graphs with combined multiple edges , in which each edge has a natural number as multiplicity. The edges of such graphs can be represented by a multiset : a map with a set and a map that assigns a positive number called a color to each node . Graphs with colored nodes and / or edges are similar .
4. Of weighted nodes and / or edges: We speak of weights instead of colors when the mapping is real-valued. In Node Weighted this corresponds to a fuzzy set , wherein is a real valued multiset . The same applies to weighted edges. For oriented graphs this means in particular that the set of edges (a relation, i.e. set of ordered pairs of nodes) becomes a multi-set or fuzzy set in an extension of the relation concept.
Examples
Properties of two-digit relations
General relations
Overview of the properties
The following relations are important for functions (represented as special relations). In general, here the relationship between two different amounts of the case is also possible.
| The relation is called | if and only if (predicate logic) | or equivalent (quantity notation) | and that means: |
|---|---|---|---|
|
left total or final (multifunction) |
Every item from has at least one partner in | ||
| right total or surjective | Every item from has at least one partner in | ||
| left unambiguous or injective | Each element from has at most one partner in | ||
|
(legally) unambiguous (partial function) |
Each element from has at most one partner in |
| The relation is called | if and only if (predicate logic) | or equivalent (quantity notation) | and that means: |
|---|---|---|---|
| bitotal | Every element out has at least one partner in and vice versa. | ||
| unambiguous | Each element out has at most one partner in and vice versa. | ||
| bijective | Each element from has exactly one partner in | ||
| Figure or function | Each element from has exactly one partner in |
Alternative ways of speaking
One also says
- left full instead of left total ,
- right complete instead of right total ,
- unambiguous instead of unambiguous to the left,
- subsequently unambiguous instead of right unambiguous,
A right-unambiguous or functional relation is also called a partial function . If this is also left total - i.e. a function - then for clarity it is also called total function.
Functions
Overview of functional properties for relations
A relation is therefore a (total) function if and only if it is left total and right unambiguous. This means that every element in A has exactly one partner in B. The properties surjective, injective and bijective are usually used for functions and specify certain additional properties. For example, a function (and any relation) is bijective if and only if it is surjective and injective, i.e. if its inverse relation is a function.
| The relation is called | exactly when she is a | is or equivalent (quantity notation) | and that means: |
|---|---|---|---|
| Surjection | surjective function | Every element from has exactly one partner in and every element from has at least one partner in | |
| injection | injective function | Each element from has exactly one partner in and each element from has at most one partner in | |
| Bijection | bijective function | Each element out has exactly one partner in and vice versa. |
Inverse function
A mapping or function is also called
- reversibly unambiguous or reversible if it is bijective .
A function is always reversible as a relation, but as a function it is reversible exactly when its reverse relation is also a function, i.e. when there is an inverse function of it.
Homogeneous relations
The examples given in the following tables refer to the normal arrangement of real numbers when using the equal sign “=”, the less than sign “<” and the less than or equal sign “≤”.
| The relation is called | if and only if (predicate logic) | or equivalent (quantity notation) | and that means: |
|---|---|---|---|
| right comparative or third equal | If two elements are each related to the same third element, then they are also related to each other. For example, with and always applies | ||
| left-hand comparative or Euclidean | If a first element is related to a second and a third element, then these are also related to one another. For example, with and is always the same | ||
| transitive | If a first element is related to a second element and this in turn is related to a third element, then the first element is also related to the third element. For example, it follows from and always | ||
| intransitive | If two elements are related and the second element is related to a third element, then the first element is not related to the third element. E.g. every natural number is the (immediate) predecessor of and the (immediate) predecessor of but is not the (immediate) predecessor of |
Non- transitivity (i.e. the relation is not transitive), intransitivity, and negative transitivity are each different from one another.
| The relation is called | if and only if (predicate logic) | or equivalent (quantity notation) | and that means: |
|---|---|---|---|
| reflexive | Each element is related to itself, e.g. B. is always | ||
| irreflexive | No element is related to itself, e.g. B. applies to none |
| The relation is called | if and only if (predicate logic) | or equivalent (quantity notation) | and that means: |
|---|---|---|---|
| symmetrical | The relation is undirected, e.g. B. it always follows from (and vice versa) | ||
| antisymmetric or identitive | There are no two different elements that are related in both directions, e.g. B. follows from and always | ||
| asymmetrical | There are no two elements that are related in both directions, e.g. B. it always follows that it does not hold. |
| The relation is called | if and only if (predicate logic) | or equivalent (quantity notation) | and that means: |
|---|---|---|---|
| total or completely | Every two elements are related, e.g. B. if always or applies. | ||
| konnex or connected | Two different elements are related, e.g. B. if always or also if always or applies. | ||
| trichotome | Every two different elements are always related in exactly one way, e.g. B. if always either or applies. |
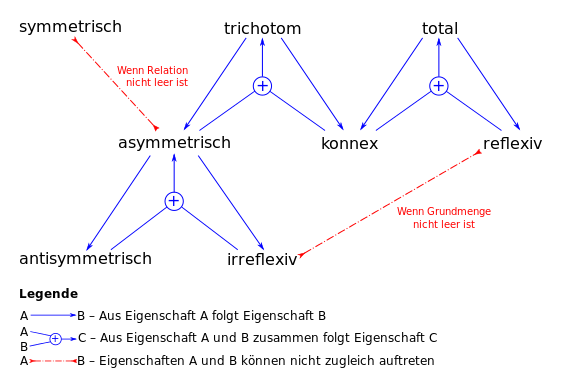
The following relationships apply between the properties:
The following relationships exist between the properties of a relation and those of its complement :
- is reflexive is irreflexive (and vice versa).
- is symmetrical is symmetrical.
- is antisymmetric is connex (and vice versa).
- is total is asymmetrical (and vice versa).
Classes of relations
Other important classes of relations and their properties:
- Quasi-order or pre-order: transitive and reflexive
- Compatibility relationor tolerance relation: compatible (reflexive and symmetrical) (English: in the finite case dependency relation , in the transfinite case tolerance relation ).
- Equivalence relation : transitive, reflexive and symmetrical
- Partial order / partial order , partial order or order: transitive, reflexive and antisymmetric.
- Full order / total order or linear order: transitive, reflexive, antisymmetric and total
- Well-ordering : a linear order in which each non-empty subset of A, a smallest element has
- Strict order or strict partial order / partial order: transitive, irreflexive and antisymmetric (i.e. asymmetric)
- Strict full order / total order or linear strict order: transitive, irreflexive, antisymmetric and connex
Relation sign
In elementary mathematics there are three basic comparative relations:
- (Example: "2 is less than 3")
- (Example: "3 equals 3")
- (Example: "3 is greater than 2")
with .
Two real numbers are always in exactly one of these relationships. With these relation symbols, others can also be formed. The following applies:
- , if or (example: "4 is not greater than 5")
- , if or (example: "5 is not less than 5")
- , if or (example: "4 is not equal to 5")
for everyone .
The above order relations do not exist for complex numbers .
Mathematicians also use the sign ≤ for abstract order relations (and ≥ for the associated inverse relation) while “<” is not an order relation in the sense of the mathematical definition.
For equivalence relations , “symmetrical” symbols such as ≈, ~, ≡ are preferred.
Category theory
For any half-ring with zero element and one element , the following is a category :
- .
- A morphism is a function .
- The following applies to
objects
- .
- This is identical to the Kronecker delta : .
- The following applies to
objects and morphisms
- .
The morphisms are set-indexed matrices and their composition happens as with matrix multiplication , corresponds to the unit matrix .
In special cases , d. i.e., is the category of relations.
application
Operations on whole relations are examined in relational algebra . In computer science , relationships are important when working with relational databases .
See also
literature
- Garrett Birkhoff : Lattice Theory . 3. Edition. AMS, Providence, RI 1973, ISBN 0-8218-1025-1 .
- Stefan Brass: Mathematical Logic with Database Applications . Martin Luther University Halle-Wittenberg, Institute for Computer Science, Halle 2005, p. 176 ( informatik.uni-halle.de [PDF]).
- Marcel Erné: Introduction to Order Theory . Bibliographisches Institut, Mannheim 1982, ISBN 3-411-01638-8 .
- Helmuth Gericke: Theory of Associations . Bibliographical Institute, Mannheim 1963.
- Dieter Klaua : set theory . De Gruyter, Berlin / New York 1979, ISBN 3-11-007726-4 (The author uses the term correspondence in the set-theoretical sense synonymously with relation, but then uses the symbol instead of . In the article here, however, or (graph of ) written).
- H. König: Design and structural theory of controls for production facilities (= ISW Research and Practice . Volume 13 ). Springer, Berlin / Heidelberg 1976, ISBN 3-540-07669-7 , pp. 15-17 , doi : 10.1007 / 978-3-642-81027-5_1 .
- Ingmar Lehmann , Wolfgang Schulz: Sets - Relations - Functions . A clear introduction. 3rd, revised and expanded edition. Vieweg + Teubner, Wiesbaden 2007, ISBN 978-3-8351-0162-3 .
- Heike Mildenberger: Axiomatic set theory . University of Freiburg, November 9, 2015, p. 58 ( mathematik.uni-freiburg.de [PDF]).
- Willard van Orman Quine : Set theory and its logic (= logic and foundations of mathematics . Volume 10 ). Vieweg + Teubner, Wiesbaden 1973, ISBN 3-528-08294-1 , pp. 264 (American English: Set Theory And Its Logic . Cambridge, MA 1963. Ullstein 1978 paperback).
- Gerard O'Regan: Guide to Discrete Mathematics. Sets, Relations and Functions (= Texts in Computer Science (TCS) ). Springer, Switzerland 2016, p. 25–51 , doi : 10.1007 / 978-3-319-44561-8_2 ( springer.com [PDF; 1000 kB ]).
- Fritz Reinhardt, Heinrich Soeder: dtv atlas mathematics . 11th edition. tape 1 : Fundamentals, Algebra and Geometry. Deutscher Taschenbuchverlag, Munich 1998, ISBN 3-423-03007-0 , p. 30-33, 42-45 .
- Gunther Schmidt, Thomas Ströhlein: Relations and graphs . Springer, Berlin a. a. 1989, ISBN 3-540-50304-8 .
- Robert Wall: Introduction to Logic and Mathematics for Linguists . tape 1 : Logic and set theory . Librarian, Kronberg / Ts. 1974, ISBN 3-589-00023-6 .
- Siegfried Wendt: Non-physical basics of information technology - interpreted formalisms . 2nd Edition. Springer, Berlin / Heidelberg 2013, ISBN 978-3-540-54452-4 , doi : 10.1007 / 978-3-642-87627-1 ( books.google.de ).
Web links
- Literature on relation in the catalog of the German National Library
- Video: Idea of the two-digit relations . University of Education Heidelberg (PHHD) 2012, made available by the Technical Information Library (TIB), doi : 10.5446 / 19788 .
References and comments
- ↑ a b G. Smolka: Programming: Chapter 2 - Set theory , at: Saarland University, May 20, 2003, § 2.5. Binary relations, p. 15.
- ↑ Walter Gellert, Herbert Kästner , Siegfried Neuber (eds.): Lexicon of Mathematics. Bibliographisches Institut Leipzig, 1979, p. 484.
- ↑ a b Albert Monjallon: introduction to modern mathematics. Edition 2. Springer-Verlag, 2013, ISBN 978-3-663-16043-4 , p. 74. doi: 10.1007 / 978-3-663-16043-4 , (books.google.de)
- ^ A b Wilhelm Dangelmaier: Production Theory 1: Methodical Basics. Springer-Verlag, 2017, ISBN 978-3-662-54922-3 , p. 478. doi: 10.1007 / 978-3-662-54923-0 (books.google.de)
- ↑ a b Cobocards: pre-area and post-area.
- ↑ a b Matheboard: Relations: What exactly is meant by the pre / post range of a relation?
- ↑ Dieter Klaua: Set theory. Page 62, definition 5 (1st part).
- ↑ a b c H. König: Design and structure theory of controls for production facilities. Page 19.
-
↑ Further notations :, in the English-language literature :, see: Gerard O'Regan: Sets, Relations and Functions. P. 36.
- ↑ Dieter Klaua: Set theory. Page 62, definition 5, (2nd part).
-
↑ Further notations :, in the English-language literature
:, see: Gerard O'Regan: Sets, Relations and Functions. P. 36.
- ↑ Dieter Klaua: Set theory. Page 62, definition 5, (3rd part).
- ↑ In the theory of algebraic structures - especially with regard to category theory, the terms domain and codomain are mostly used in the sense of source and target sets, while in introductory writings on set theory these are usually defined as archetypes and images,
- ↑ also amount similar , quantitative manner , to ger .: left-narrow or set-like called, see Wikibooks: Mathematics Glossary: Mathematical attributes: small predecessor
- ↑ Heike Mildenberger 2015, p. 59f.
- ↑ Martin Ziegler: Lecture on set theory , University of Freiburg, 1992–2014, p. 12.
- ^ Azriel Levy: Basic Set Theory (= Dover Books on Mathematics . Volume 13). Courier Corporation, Newburyport 2012, ISBN 978-0-486-15073-4 , p. 22, (online)
- ↑ If primitive elements are allowed: for primitive elements there is also a set.
- ↑ See also: Axiomatic Set Theory, Getting a model of (ZF - Fnd) ∪ {¬Fnd} from a model of ZF , Ben Gurion University (BGU) of the Negev, The Department of Mathematics, 2003.
- ↑ In the general case with the support amount sequence is the Allrelation , in the homogeneous case, with the n times the support amount is .
- ↑ Stefan Brass (2005), p. 19.
- ↑ The characteristic function as a truth function therefore corresponds to a logical predicate , and in model theory the relation symbols are therefore also called predicate symbols, see Stefan Brass (2005) p. 16.
- ↑ English: forward relational composition
- ^ Mathematics Stack Exchange: Forward and backward composition in relational algebra Discussion of the chaining directions in connection with the chaining of functions as special relations. The Maplet notation is sometimes used for ordered pairs :
- ↑ a b c Glossary of Z notation §Relations , University of Washington
-
↑ Occasionally there is also the semicolon in outline representation. Depending on the hardware and settings, it is not always displayed correctly in Wikipedia.
- ↑ English: backward relational composition
- ↑ a b H. König: Design and structure theory of controls for production facilities. Page 21.
- ↑ a b c W. v. O. Quine: Set theory and its logic. Page 47.
- ^ Relational algebra. In: Mathepedia.de.
- ↑ Also noted as bijection .
- ↑ For notation, see Gary Hardegree: Set Theory, Chapter 2: Relations , University of Massachusetts, Amherst, Department of Philosophy, Fall 2015, p. 11: D16 and D17. In contrast to the other notations, these symbols reference images (functions) between the power sets .
- ↑ Analogous to: D. Klaua: Set theory. P. 63, definition 6 (a).
- ↑ In the case of order relations and the like, some authors also speak of a predecessor set or class, see Heike Mildenberger 2015, p. 6, definition 1.12.
- ↑ W. v. O. Quine: Set theory and its logic. Page 17. Attention: The printout is titled as image , but it clearly defines the original image (a set of left-hand coordinates = arguments ). Note that this notation is used contrary to functions here, with functions it stands for the image (a set of right-hand coordinates = function values ) of a set under a function . Functions are special relations. See picture (math) §Alternative notations .
- ↑ Johannes Köbler: Introduction to Theoretical Computer Science: Relations. Humboldt University Berlin, Institute for Computer Science WS2013 / 14, p. 68.
- ↑ W. v. O. Quine: Set theory and its logic. Page 17.
- ↑ Following the detailed relationship definition above, one will understand the diagonal as the graph of identity: (Relation) with (Graph).
- ↑ Following the above detailed relation definition, analogous to the diagonal, the Nabla will be understood as the graph of the all relation: (Relation) with (Graph)
- ↑ This can lead to confusion with the Cartesian product with lead. The meaning results from the context in each case.
- ^ A b Gerard O'Regan: Sets, Relations and Functions. P. 39.
- ↑ See also: Kleenesche envelope .
- ↑ For the transitivity properties of these associations see Proving that is a transitive relation on A , on: StackExchange: Mathematics 2018.
- ^ Robin Hirsch, Ian Hodkinson: Relation algebras. P. 7, on: Third Indian Conference on Logic and its Applications (ICLA). 7-11 January 2009, Chennai, India.
- ↑ The links (one-digit) and (two-digit) are - strictly speaking - the restrictions on or meant.
- ^ C. Brink, K. Britz, RA Schmidt: Peirce Algebras. (1994), pp. 163f. In: M. Nivat, C. Rattray, T. Rus, G. Scollo (Eds.): Algebraic Methodology and Software Technology (AMAST'93). Workshops in computing. Springer, London.
- ↑ The term graph in the graph-theoretical sense is to be distinguished from the term graph of a relation according to the detailed definition of relations mentioned at the beginning (as well as images), which is not used in graph theory.
-
↑ The term color stems from the fact that the number understood as multiplicity according to the multimetary theory is reproduced in the visual representation as a number-coded color of the edge , analogously with colored nodes . An example of color numbers would be the RAL colors .
- ↑ WD Blizard: Real-valued Multisets and Fuzzy Sets. In: Fuzzy Sets and Systems. Vol. 33, 1989, pp. 77-97. doi: 10.1016 / 0165-0114 (89) 90218-2 .
-
↑ "Two quantities that are equal to one and the same third are equal to one another." Cf.
Henri Poincaré: Wissenschaft und Hypothese. Author. German edition with ext. Note from F. u. L. Lindemann. Teubner, Leipzig 1904, p. 36. - ↑ Wolfgang Rautenberg: Introduction to Mathematical Logic. A textbook. Vieweg + Teubner, Wiesbaden 2008, ISBN 978-3-8348-0578-2 , p. 42.
- ↑ The 1st axiom in Euclid's Elements can, however, also be seen as synonymous with third equals .
- ↑ It is not uncommon for konnex to be defined as total .
- ↑ This can easily be seen from the tables above (1st and 2nd column) taking into account , i. H. and the predicate logic rules. The inversions apply because of involutivity .
- ↑ Wendt 2013, page 31


















































































































![{\ displaystyle R [Y]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9ca7f0a1fdfe689def5adb90032f7da6c9ffc93)


![{\ displaystyle R [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33ac134e157437a3986ad725151bf8e5fe566156)
![{\ displaystyle [a] _ {R} = R \ langle \ {a \} \ rangle = R ^ {- 1} \ langle \ {a \} \ rangle}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bc947079ddacce3198f75fca059a2f3ad5e4332)




























































![{\ displaystyle f \ colon \; M \ to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/981c1ffde3d83759978efcfb0871056111d361cd)