permutation
Under a permutation (from latin permutare , reverse ' ) is understood in the combinatorics an arrangement of objects in a specific order . Depending on whether or not certain objects are allowed to appear several times, one speaks of a permutation with repetition or a permutation without repetition. The number of permutations without repetition results as a factorial , while the number of permutations with repetition is given via multinomial coefficients .
In group theory , a permutation without repetition is a bijective self-mapping of a usually finite set , whereby the first natural numbers are usually used as reference sets. The set of permutations of the first natural numbers forms the symmetrical group of degree with the consecutive execution as a link . The neutral element of this group represents the identical permutation, while the inverse element is the inverse permutation. The subgroups of the symmetric group are the permutation groups .
Important parameters of permutations are their cycle type , their order and their sign . With the help of the missing positions of a permutation, a partial order can be defined on the set of permutations of fixed length . Using its inversion table , each permutation can also be assigned a unique number in a faculty-based number system . Important classes of permutations are cyclic , fixed-point-free , self-inverse and alternating permutations .
Permutations have a wide range of uses within and outside of mathematics , for example in linear algebra ( Leibniz formula ), analysis ( rearrangement of rows ), graph theory and game theory , cryptography ( encryption method ) , computer science ( sorting method ) and quantum mechanics ( Pauli Principle ).
Combinatorial basics
Problem
A permutation is an arrangement of objects in a certain order or a rearrangement of objects from a given order. Examples of permutations are:
- An anagram is a permutation of the letters in a word, such as GRANDSON and CARNATION.
- The shuffling of the cards in a deck of cards is (ideally) a random permutation of the cards.
- In volleyball , changing position after conquering the right to serve is a cyclical permutation of the players.
- Many sorting methods work with successive transpositions, i.e. permutations that exchange exactly two objects.
If not all objects are selected in such an arrangement, one speaks of a variation instead of a permutation ; the sequence in the selection does not matter, of a combination . In counting combinatorics , the question of the number of possible permutations arises. A distinction is made here between the case that all objects are different and the case that some of the objects are identical.
Permutation without repetition
A permutation without repetition is an arrangement of objects that are all distinguishable. Since there are placement options for the first object, there are only options for the second object , for the third object only and so on up to the last object, which only has a free space. The number of possible permutations of objects is therefore given by the factorial
specified.
For example, there are possible arrangements of four different colored balls in a row.
Permutation with repetition
A permutation with repetition is an arrangement of objects, some of which are indistinguishable. If exactly the objects are identical, they can be exchanged in their places without resulting in a new order. In this way, arrangements are exactly the same. The number of permutations of objects, of which are identical, is therefore given by the decreasing factorial
given. If there is not just one, but groups with identical objects, then all of these objects can be exchanged in their places without creating new arrangements. If one also counts the objects that only occur once with a multiplicity , then the following applies and the number of possible permutations is given by the multinomial coefficient
specify.
For example, there are possible arrangements of four colored balls in a row if exactly two of the balls have the same color, and possible arrangements if two balls are each of the same color .
definition
Let be a set with elements , then a -digit permutation (without repetition) is a bijective map
- ,
which assigns an element of the same set to each element of the set. Vividly takes each element of the permutation for the place of its associated element one. Due to the bijectivity of the mapping, two different elements are never mapped onto the same element. The case is also admissible and is then the empty set .
Since, by definition, every finite set is equal to a set of the form {1, 2, ..., n} , one can always restrict oneself to the first natural numbers as a reference set when considering permutations mathematically . A permutation is then a bijective mapping
- ,
which assigns every natural number between and exactly one number in the same range. If you imagine all the numbers in a list, then the number takes the place with the number through the permutation .
notation
Two-line form
In the detailed representation of a -digit permutation , this is written as a matrix with two rows and columns. In the top line are the numbers from to (in any order). The function value is then located under each number in the second line :
The second line also contains every number from to exactly once.
example
The permutation with and is in the two-line form by
written down.
Tuple notation
With the more compact tuple notation, you just write the function values in one line:
This notation therefore only uses the second line of the two-line form. Since the information about the number that is mapped to is lost, the tuple notation can only be used if the order of the numbers from the first line is known. Usually this is the natural order. The tuple notation can easily be confused with the cycle notation (see following section), especially since some authors leave out the commas.
example
The tuple notation is used for the above example permutation
- .
Cycle notation
The cycle notation also only requires one line. You start with any number and write
- ,
where the -fold execution of denotes and the smallest natural number is with . Such a bracket is called a cycle and is its length. If there are other numbers that have not yet been noted, choose such a number and write another cycle of length after it. You go on until you write down each number exactly once. Brackets containing only one number can then be deleted again. This representation is not clear, because the order of the cycles can be selected as desired and the numbers can be interchanged cyclically in each cycle.
example
The following cycle notation is used for the above example permutation:
Further representations
Graph representation
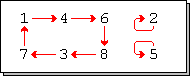
The graph of a -digit permutation is a directed graph with a set of nodes and a set of edges
- .
In such a graph, each node has exactly one outgoing and exactly one incoming edge. The cycles of the graph are precisely the cycles of the permutation, with the numbers that are held by the permutation creating loops at the associated nodes. The graph of a permutation is only connected if the permutation consists of a single cycle of length .
Permutation matrices
|
Permutation matrix of the permutation
|
The permutation matrix of a -digit permutation is given by
Are defined. If the number is mapped onto the number by a permutation , then the associated permutation matrix in the -th row has one in the column . The elements of a column vector are in linear algebra permuted characterized in that the vector from the left by the permutation matrix multiplied is:
- .
Permutations as a group
The permutations of the set form a group with the sequential execution as a link , the symmetrical group . The symmetrical groups play an important role in mathematics. For example, according to Cayley's theorem, every finite group is isomorphic to a subgroup of a symmetric group . The subgroups of the symmetric group are called permutation groups .
The Galois group in (classical) Galois theory is such a subgroup of the symmetrical group: The zeros of polynomials are permuted . The properties of the Galois group provide information about the solvability of a polynomial equation by radicals, i.e. H. by root expressions. This can be used to prove, for example, that the general polynomial equation of the fifth or higher degree cannot be solved by radicals ( Abel-Ruffini theorem ).
composition
Two -digit permutations can be carried out one after the other by first applying the first permutation and then applying the second permutation to the result. The sequential execution is written as
- ,
applying first and then . This sequential execution is also called composition , linkage or product of two permutations and the result is again a -digit permutation. The composition of permutations is not commutative , that is, in general, and give different results. The symmetric group is therefore not Abelian . However, the composition is associative, i.e. it applies to all permutations
- .
Examples
It is for example
- .
To get the result, you apply the permutations from right to left and follow the path of the individual numbers. This is mapped to itself in the second permutation and then to the , that is , as a whole in the first permutation . The way is corresponding , so . The finally goes the way , in the result .
The cycle display is analogous, whereby numbers that do not appear in a cycle are recorded. For example is
- .
Here we determined the paths , , and .
Identical permutation
The neutral element of the symmetric group is the identical permutation
- ,
that is, the permutation that leaves all numbers in their place. So for every permutation
- .
The identical permutation is also noted as empty brackets , as or as . The permutation matrix of the identical permutation is the identity matrix . The identical permutation graph has only one loop at each node. The identical permutation of length one is also known as the trivial permutation.
Inverse permutation
For every permutation there is exactly one inverse element , the inverse permutation , with
- .
The inverse permutation is obtained by exchanging the upper and lower lines in the two-line form:
In the cycle notation, the inverse permutation is obtained by writing the numbers in the reverse order in each cycle. In the graph of the inverse permutation, only the directions of all edges are reversed. The permutation matrix of the inverse permutation is the transposed matrix of the initial permutation .
example
The inverse permutation to
is
- .
conjugation
Two permutations are said to be conjugated to each other if a permutation exists such that
- or.
applies. Is the permutation the number to the number displayed, then the permutation is the number to the number from. The conjugation represents an equivalence relation on the set of permutations of fixed length, that is, it is reflexive ( ), symmetric (from follows ) and transitive (from and follows ). The set of all permutations conjugated to a permutation form an equivalence class (the conjugation class ), which is noted by.
example
The symmetrical group has the three conjugation classes:
Parameters
Cycle type
| Cycle type | Cycle structure | number | |
|---|---|---|---|
| 1 | 1 1 | (•) | 1 |
| 2 | 1 2 | (•) (•) | 1 |
| 2 1 | (• •) | 1 | |
| 3 | 1 3 | (•) (•) (•) | 1 |
| 1 1 2 1 | (• •) (•) | 3 | |
| 3 1 | (• • •) | 2 | |
| 4th | 1 4 | (•) (•) (•) (•) | 1 |
| 1 2 2 1 | (• •) (•) (•) | 6th | |
| 2 2 | (• •) (• •) | 3 | |
| 1 1 3 1 | (• • •) (•) | 8th | |
| 4 1 | (• • • •) | 6th |
Denoted for the number of cycles of the length in a permutation , then the cycle type of this permutation is the formal expression
- ,
whereby the terms do not have to be listed with. Formal here means that the product and the potencies are not actually calculated. The number of possible cycle types with -digit permutations corresponds to the number of partitions of the number . The number of permutations per cycle type can be calculated from the type description. The inverse permutation always has the same cycle type as the initial permutation. In addition, the result of composing two permutations has the same cycle type regardless of the order of the operands. Accordingly, two permutations are conjugated to each other if and only if they are of the same cycle type. The permutations of the same cycle type therefore form the conjugation classes of the symmetrical group . The permutations with the same number of cycles are counted by the Stirling numbers of the first kind.
order
The order of a permutation is the smallest natural number in such a way that executing one after the other results in the identical permutation:
- .
The order of a permutation is thus the element order of as a group element of the symmetrical group. From the cycle representation of a permutation, the order can be determined as the smallest common multiple of the lengths of the disjoint cycles. For example, the order of the permutation is the least common multiple of three and two, i.e. six.
Deficiencies
| No. | permutation | Deficiencies | number |
|---|---|---|---|
| 0 | (1,2,3) | - | 0 |
| 1 | (1,3,2) | (2.3) | 1 |
| 2 | (2,1,3) | (1.2) | 1 |
| 3 | (2,3,1) | (1.2), (1.3) | 2 |
| 4th | (3.1.2) | (1.3), (2.3) | 2 |
| 5 | (3.2.1) | (1,2), (1,3), (2,3) | 3 |
A pair of numbers is called an error or inversion of a permutation , if and applies. So two numbers form an error if and only if the larger one comes before the smaller one after applying the permutation. The set of deficiencies in a permutation is thus through
given. The number of faults in a permutation is called the fault number or inversion number of the permutation. The missing number can be viewed as a measure of the disorder of the numbers swapped by the permutation.
sign
The sign of a permutation is the number
- .
A permutation thus has the sign if its missing number is even, otherwise the sign . In the first case one speaks of an even and in the second case of an odd permutation. The set of even permutations forms a subgroup of the symmetrical group , the alternating group .
Ascents and descents
An increase in a permutation is a number for which holds. The set of increases in a permutation is thus through
given. The same applies to a descent . The number of permutations in with exact increases or decreases is given by the Euler numbers . A maximum, that is to say no longer extendable on both sides
successively increasing or decreasing numbers in a permutation is called increasing or decreasing run of length . For such a sequence can only consist of one number. If a permutation has a total of ascents or descents, it is composed of descending or ascending runs. Accordingly, the number of permutations in with exactly increasing or decreasing runs is given by.
Order properties
arrangement

Using the wrong objects can be on the set of one -bit permutations partial order by
- ,
define, where are. The minimum element with respect to this order is the identical permutation, while the maximum element is the permutation which reverses the order of all numbers. In the associated Hasse diagram , two permutations are connected by an edge if they emerge from one another through a neighboring exchange. The nodes and edges of the Hasse diagram form a Cayley graph that is isomorphic to the edge graph of the corresponding permutahedron . The permutahedron is a convex polytope in -dimensional space, which arises from the fact that the permutations of the set are interpreted as coordinate vectors and then the convex hull of these points is formed.
enumeration
The inversion table or the inversion vector of a permutation assigns to each number the number of faults it generates. Designates the number of numbers that are to the left of in the tuple representation and are greater than , then the inversion vector of a permutation is through
given. Conversely, the underlying permutation can be clearly determined from the inversion vector. Summing up the inversion vector as a number in a faculty-based number system on, every permutation can be a unique number by
to assign. Instead of the inversion vector, the Lehmer code is also used to number permutations.
Symmetries
The permutation complementary to a permutation is
- .
The complementary permutation is created by horizontally mirroring the permutation matrix. The reverse permutation is similar
and is created by vertical reflection. Complementary and reverse permutations have the same cycle type and order as the initial permutation. However, the number of ascents and descents is swapped for complementary and reverse permutations. In addition, the sign is reversed for complementary permutations and for reverse permutations with length 2 modulo 4 or length 3 modulo 4. The inverse of the complementary permutation is equal to the reversed inverse and the inverse of the reverse permutation is equal to the complementary inverse.
Special permutations
Cyclic permutations
A permutation that cyclically swaps numbers and leaves the remaining numbers fixed is called a cyclic permutation or cycle and is written as a single cycle of length . A cycle, i.e. an exchange of two numbers, is also called transposition. The concatenation of cyclic permutations is commutative if they have disjoint carriers. The inverse of a cyclic permutation is always cyclic as well, as is the powers of a cyclic permutation whose length is a prime number. Every cyclic permutation can be broken down into individual (not disjoint) transpositions and has an even sign if and only if its length is odd.
Fixed point free permutations
Numbers that are held by a permutation are called fixed points of the permutation. In the two-line form, fixed points can be recognized by the fact that the top and bottom entries of the respective column are the same. In the cycle notation, fixed points are exactly the units' cycles or the numbers that do not appear. In the permutation matrix, the entries assigned to the fixed points are the main diagonal . A fixed point-free permutation does not hold any of the numbers and is also called derangement. The number of fixed point-free permutations of the numbers from to can be calculated by the sub-faculty . For increasing , the proportion of fixed-point-free permutations tends very quickly against the reciprocal of Euler's number . If some of the elements in a permutation are to remain in their old place, one speaks of a partial derangement, the number of which can be determined using the Rencontres numbers .
Self-inverse permutations
A permutation with or equivalent to it is called involution or self-inverse. The involutions are precisely the permutations of order two as well as the identity itself (the only permutation of order one). A permutation is an involution if and only if its cycle representation contains a maximum of cycles of length two, i.e. transpositions. The permutation matrix of a self-inverse permutation is always symmetrical . Self-inverse permutations play an important role in cryptography , namely if a message is encrypted using a self-inverse permutation, then the message can also be decrypted again using the same permutation.
An example of a self-inverse permutation is mirroring
- ,
see also word (Theoretical Computer Science) §Spiegelung und Palindrome .
Alternating permutations
A permutation is called alternating if there is no number in its tuple representation in terms of its size between the preceding number and the following number . In an alternating permutation, the numbers swapped by the permutation are therefore always alternately larger and smaller than the previous number. If the sequence of numbers begins with an increase, one speaks of an up-down permutation, and it begins with a decrease in a down-up permutation. Each alternating permutation of odd length corresponds to a full partially ordered binary tree and each alternating permutation of even length corresponds to an almost full such tree. The numbers of alternating permutations of fixed length appear as coefficients in the Maclaurin series of the secant and the tangent function and are closely related to the Euler and Bernoulli numbers .
Separable permutations
Separable permutations are permutations that can be represented as a direct or skewed sum of trivial permutations. Such a sum of two permutations results in a new permutation whose length is the sum of the lengths of the two initial permutations. In the case of a direct sum, the second permutation is attached to the first in a shifted manner; in the case of an inclined sum, the first permutation is shifted in front of the second. The number of separable permutations of fixed length is given by the Schröder numbers . Separable permutations are characterized by a special recursive block structure of the associated permutation matrices. They are examined , among other things, in sorting theory.
Random permutations
A random permutation is a permutation selected at random from the set of permutations. In stochastics , random permutations are viewed as random variables from a discrete probability space . In this way, key figures of random permutations, such as the number of fixed points, deficiencies or cycles, can be viewed as discrete random variables, the probability distributions of which are then examined. In the computer, random permutations can be efficiently generated using the Fisher-Yates method . Random permutations are examined , among other things, in the analysis of sorting processes , in cryptography and coding theory, and in the context of randomized algorithms . The 100 Prisoners Problem is a mathematical puzzle based on random permutations.
Permutation in music
About permutation in the fugue composition see under Fugue .
In twelve-tone technique , permutation is the derivation of further rows from a twelve-tone row by taking individual tones out one after the other according to a specific numerical selection mode until a new, complete twelve-tone row is created. This is how Alban Berg proceeds in his opera Lulu .
Remarks
-
↑ Occasionally also as a bijective representation
- ↑ Horst Weber: Article Permutation , in: The great Lexicon of Music , edited by Marc Honnegger and Günter Massenkeil , Herder Verlag Freiburg / Brsg. 1978/1987, Volume 6, ISBN 3-451-20948-9 , pp. 243f
literature
- Martin Aigner : Discrete Mathematics . Vieweg, 2006, ISBN 3-8348-9039-1 .
- Michael Artin : Algebra . Birkhäuser, 1998, ISBN 3-7643-5938-2 .
- Albrecht Beutelspacher : Linear Algebra . 6th revised and supplemented edition. Vieweg, 2003, ISBN 3-528-56508-X .
- Konrad Jacobs , Dieter Jungnickel : Introduction to combinatorics . de Gruyter, 2003, ISBN 3-11-016727-1 .
- Hans Kurzweil, Bernd Stellmacher : Theory of finite groups: an introduction . Springer, 1998, ISBN 3-540-60331-X .
- Kristina Reiss , Gernot Stroth : Finite Structures . Springer, 2011, ISBN 3-642-17181-8 .
Web links
- DA Suprunenko: Permutation of a set . In: Michiel Hazewinkel (Ed.): Encyclopaedia of Mathematics . Springer-Verlag , Berlin 2002, ISBN 978-1-55608-010-4 (English, online ).
- alozano, Pedro Sanchez, Raymond Puzio, J. Pahikkala: Permutation . In: PlanetMath . (English)
- Eric W. Weisstein : Permutation . In: MathWorld (English).










































































































![\ left [\ pi \ right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f958743da6e81556905888759ac1580dd66f0af)

![[\ operatorname {id}] = \ {\ operatorname {id} \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a972170ffb2c187571e4c5af3e5d759433e3a7a1)
![[(1 ~ 2)] = \ {(1 ~ 2), (1 ~ 3), (2 ~ 3) \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/253f503be0a4228785182e4af4022425984510b6)
![[(1 ~ 2 ~ 3)] = \ {(1 ~ 2 ~ 3), (1 ~ 3 ~ 2) \}](https://wikimedia.org/api/rest_v1/media/math/render/svg/958a3b1fb22d420834b91c32f2de0678ba29486d)