Hasse diagram

In mathematics , a Hasse diagram (also called order or simply line diagram ) is a specific graphic representation of finite, semi-ordered sets . Such diagrams are named after the mathematician Helmut Hasse .

The Hasse diagram for a partial order is the representation of a directed graph , with the elements of forming the nodes . Two nodes and are connected by an edge if applies and there is no node with (here is to be understood as and .) The restriction to such is called transitive reduction of the partial order. The direction of the edge is expressed by the fact that the node is above . Such an arrangement can be achieved because the Hasse diagram is cycle-free. Loops at reflexivity are omitted. ${\ displaystyle (M, \ leq)}$ ${\ displaystyle M}$ ${\ displaystyle a}$ ${\ displaystyle b}$ ${\ displaystyle a <b}$ ${\ displaystyle c}$ ${\ displaystyle a <c <b.}$ ${\ displaystyle a <b}$ ${\ displaystyle a \ leq b}$ ${\ displaystyle a \ not = b}$ ${\ displaystyle a, b}$ ${\ displaystyle b}$ ${\ displaystyle a}$

Sometimes Hasse diagrams are also used to represent strict orders (order relations of the second kind).

Examples

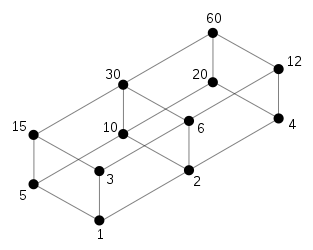
Divider association

The divisors of a natural number can be represented by means of a Hasse diagram, since they form a semi-ordered set, the divisor lattice , with regard to the divisibility relation . In this case, the diagram is also called the divider image . The following picture shows the Hasse diagram of the divisors of 60.

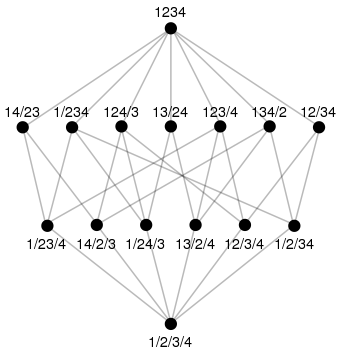
Partitions

The set of partitions of the set {1, 2, 3, 4} with the fineness as a partial order.

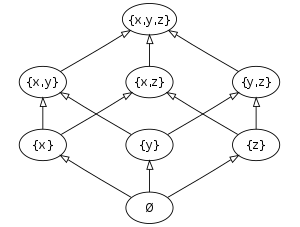
Power set

The -element power set of a -element set with the set inclusion can be represented as a Hasse diagram. The elements of the power set form the nodes and two elements are connected by an edge if they are in a subset relation. The empty set represented by the lowest node is a subset of all elements; the universe represented by the top node is a superset of all elements. ${\ displaystyle 2 ^ {n}}$ ${\ displaystyle n}$

The arrangement of the sets, which contain the same number of elements, on the same level of the Hasse diagram is particularly clear and widespread. It is also common and advisable to lexicographically order the sets in the levels from left to right .

A small example of a Hasse diagram of a power set is given by the set : ${\ displaystyle \ {x, y, z \}}$

A somewhat more complex diagram is obtained with the sixteen-element power set of a four-element set. It is of particular importance for propositional logic and set theory . Your closest representation in the manner described is the left of the three graphics, which shows the rhombic dodecahedral three-dimensional shadow of the four-dimensional cube . The other two graphs to the right of the rhombic dodecahedral also show possible Hasse diagrams of the power set of a four-element set, which can be more suitable for some purposes than stratification according to the number of elements. There are no graphic representations that are equally ideal for all purposes. When dealing with a particular topic, suitable Hasse diagrams often have to be found first.

Web links

Commons : Hasse diagrams - collection of pictures, videos and audio files

Weisstein, Eric W .: Hasse Diagram . In: MathWorld (English).
Video: Hate Diagrams (Part 1) . University of Education Heidelberg (PHHD) 2012, made available by the Technical Information Library (TIB), doi : 10.5446 / 19863 .

Individual evidence

↑ Helmut Hasse: About the class number of Abelian number fields. Akademie-Verlag, Berlin 1952, p. 137, footnote 2.

[1] Helmut Hasse: About the class number of Abelian number fields. Akademie-Verlag, Berlin 1952, p. 137, footnote 2.