Tesseract
| Tesseract (8-cell) 4-cube |
|
|---|---|
 Flail diagram |
|
| group | Regular polytopes |
| family | Hypercube |
| Cells | 8 ( 4.4.4 ) |
| Surfaces | 24 {4} |
| edge | 32 |
| Corners | 16 |
| Schläfli symbols | {4,3,3} {4,3} x {} {4} x {4} {4} x {} x {} {} x {} x {} x {} |
| Coxeter-Dynkin diagrams |
|
| Symmetry group | B 4 , [3,3,4] |
| properties | convex |
The tesseract [ ˈtɛsərakt ] (from ancient Greek τέσσερες ἀκτίνες tésseres aktínes , German 'four rays' ) is a transfer of the classic cube concept to four dimensions . One also speaks of a four- dimensional hypercube . The tesseract is to the cube like the cube is to the square . It has 16 corners, 32 edges of equal length , 24 square faces, and is delimited by 8 cube-shaped cells. These cells are also known as the boundary cube of the tesseract. In each corner, 4 edges, 6 surfaces and 4 cells meet at right angles .
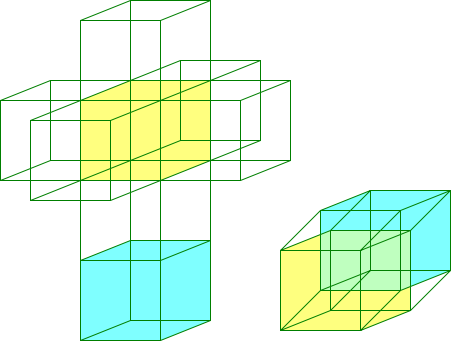
The images in this article are to be understood as images of tesseracts under parallel projections. At the bottom of the right picture you can see a blue and a yellow cube, which are connected by six further rhombohedral, distorted boundary cubes . In the three-dimensional network of the tesseract (left in the first picture) all eight delimitation cubes are folded into the three-dimensional space, just as the side surfaces of a three-dimensional cube can be unfolded into a network of six squares. There are 261 different ways to develop a tesseract.
In the following picture, a network of the tesseract can be seen on the left, and a two-dimensional parallel projection of the tesseract on the lower right.
The longest diagonal of a hypercube corresponds to the square root of its number of dimensions multiplied by its edge length. In the case of the tesseract, the longest diagonal is two edge lengths long. In a tesseract, if you stitch your eight opposing boundary cubes together in pairs, you get a 4- torus .
Projections in 2 dimensions
The construction of a hypercube can be imagined as follows:
- one-dimensional: two points A and B can be connected to form a line , a new line AB is created.
- two-dimensional: Two parallel lines AB and CD of the same length can be connected to form a square with the corners ABCD.
- three-dimensional: Two parallel squares ABCD and EFGH of the same area can be connected to a cube with the corners ABCDEFGH.
- four-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP with the same volume can be connected to form a hypercube, with the corners ABCDEFGHIJKLMNOP.
It is difficult to imagine, but it is possible to project tesseracts into three- or two-dimensional spaces. In addition, projections into the second dimension become more informative if the projected corner points are rearranged. With this method, images can be obtained that no longer reflect the spatial relationships within the tesseract, but the connection structure of the corner points, as the following examples show:
A tesseract is basically formed by two connected cubes. The scheme is similar to the construction of a cube of two squares: you place two copies of the lower-dimensional cube next to each other and connect the corresponding vertices. Each edge of a tesseract is of the same length. Eight cubes that are connected to each other.
Tesseracts are also two-part graphs, just like lines, squares, and cubes.
Projections in 3 dimensions

The cell-first parallel projection of the tesseract into three-dimensional space has a cube-shaped envelope. The closest and most distant areas are projected onto the cube and the remaining 6 cells are projected onto the square areas of the cube.
The plane -first- parallel projection of the tesseract into the 3-dimensional space has a cuboid shell. Two pairs of cells project the top and bottom halves of the envelope and the 4 remaining cells are projected onto the side surfaces.
The edge-first parallel projection of the tesseract into three-dimensional space has a shell in the shape of a hexagonal prism. Six cells are projected onto rhombic prisms, which are laid out in a hexagonal prism, analogous to how the surfaces of a 3D cube are laid out on a hexagonal shell in the corner-first projection. The two remaining cells are projected onto the bases of the prism.
The corner-first parallel projection of the tesseract into three-dimensional space has a rhombic dodecahedral shell.
Picture gallery
 Stereographic projection (the edges are projected onto a hypersphere ) |
 Simple corner graphics |
 A 3D projection of an 8 cell that performs a simple rotation around a plane dividing the figure from front left to back right and top to bottom. |
 A 3D projection of an 8-cell that performs a double rotation around two orthogonal planes. |
|
| Orthogonal projection | ||||

|

|

|
||
 A web of a tesseract. ( Watch animation .) |
 A 3D stereographic projection of a tesseract. |
|||
In media
- The science fiction short story by Robert Heinlein —And He Built a Crooked House— from 1941 is based on a building in the shape of a tesseract .
- The tesseract plays a big role in the movie Cube 2: Hypercube , in the television series Gene Roddenberry's Andromeda and in the movie Interstellar .
- In the Marvel Comics universe , a powerful, cosmic cube is named after the tesseract. Apart from the shape and the name, this item has nothing in common with the tesseract explained above. In the cinematic adaptation of the universe , the tesseract appears in the films Thor , Captain America: The First Avenger , Marvel's The Avengers , Thor: Decision Day , Avengers: Infinity War , Captain Marvel and Avengers: Endgame .
- The British rock group TesseracT named themselves after the Tesseract.
See also
literature
- Gudrun Wolfschmidt : Popularization of the natural sciences . Institute for the History of Natural Sciences, Mathematics and Technology (IGN) at the University of Hamburg. Diepholz, Verlag for the history of natural science and technology, Berlin 2002, ISBN 3-928186-59-0 , 17th chapter.
Web links
- Representation of oblique images, central projections, nets and sections of a tesseract
- Platonic polychora
- Crucifixion (Corpus Hypercubus) Painting by Salvador Dalí , which contains the web of the tesseract.
- Tesseract animated by JavaScript