4D


4D or 4-D is a common abbreviation for four-dimensional, indicating a geometric dimension .
4D is an extension of the representation of bodies in the 3D space of our experience of reality ( length-latitude-height , coordinates x, y, z) by an independent auxiliary dimension for the clear detection of the position and extent of a body. Using Cartesian coordinates x, y, z, an axis with the designation w is usually added.
The fourth dimension
The introduction of multi-dimensional " hyperspaces ", which are not accessible to our direct experience, results from the areas of higher mathematics and physics. To illustrate rooms of higher dimensions, z. B. the 3D space is expanded by an additional dimension and the representation of the body is projected into the 3D space.
In generalization of Albert Einstein's physical theories , the “fourth dimension” is assumed to be occupied by time and 4D space is equated with the term spacetime . Binding assumptions of the physical theories regarding the homogeneity of the space (according to which all dimensions are indistinguishable in terms of quality and quantity) and the observer invariance (according to which the origin of the coordinate system and the choice of the axes have no influence on the representation of the laws of nature) suggest that the Time cannot be accepted as the fourth dimension. Characteristics of space can be distinguished from those of time by using e.g. B. tries to move an observer along an axis. If the shift succeeds, the axis cannot represent the time.
Mathematically and geometrically descriptive derivation
An (additional) dimension denotes an extension in one direction that cannot be represented by other dimensions that have already been defined. On the one hand, characters in our world can have more or fewer dimensions, on the other hand, one can imagine a world that has more or fewer dimensions. The step-by-step transition from point (0D) to 1D, 2D, 3D, 4D and 5D serve as an example:
- Dimension 0
A point with no extent (a circle with radius 0). A zero-dimensional world consists of only one point.
- Dimension 1
In dimension 1 , movement away from the point is possible in any direction; one gets a route . An example is the X-axis of a coordinate system, extending to the left and right. In the one-dimensional world only this line exists, so there are only 2 possible directions.
- Dimension 2
For dimension 2 we are looking for a further direction that does not match the first segment, in the simplest case: perpendicular to the segment. For example the Y-axis of a coordinate system, stretching forwards and backwards. This gives us a coordinate system with which we can reach every point on a plane .
- Dimension 3
For dimension 3 a further direction is necessary that is not in the plane (from dimension 2). To do this, we point once (comparable to the second hand of a clock) in all directions of the plane and exclude all these directions. What remains are directions that point upwards or downwards. In the simplest case perpendicular to the plane z. B. "up". This is the Z axis of a coordinate system, extending upwards and downwards. This gives us a coordinate system with which we can reach any point in space .
- Dimension 4
Again a direction is required that is not in space (from dimension 3). To do this, we point spherically in all directions that we can imagine and exclude all these directions. What remains are directions that we cannot (no longer) imagine with our understanding of three dimensions. In the simplest case, this is perpendicular to all directions that we can imagine. If we expand the space in this direction, we have described a 4-dimensional hyperspace . For this purpose, the W-axis of a coordinate system is introduced with the extension to ana and kata , terms coined by Charles Howard Hinton .
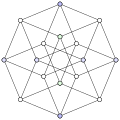
With such logical considerations one can calculate that a four-dimensional (hyper) cube ( tesseract ) has 16 corners, 32 edges, 24 surfaces and 8 volumes.
- Hypercube
Each dimension can be thought of as the composition of an infinite number of the previous dimension along the new dimension direction. The straight line, with dimension 1, is the joining of an infinite number of points of dimension 0. If you transfer these thoughts to the “fourth dimension”, this is the composition of an infinite number of (three-dimensional) spaces. The projection of a four-dimensional object is always created in three-dimensional space as a "shadow" in 3D. This must not be confused with the representation of a section of the higher-dimensional object in the lower dimension.
The shadow model (mostly as a grid model) corresponds to a model representation of the complete object while the section corresponds to an actual appearance in the lower dimension. In the event of a movement of the object, the section can therefore change over time. The development over time is therefore suitable for imagining a fourth spatial dimension. It is not the object that changes over time, only its cross-sectional image.
If one imagines a tesseract that is colored differently in the direction of the additional dimension, is aligned in this and only moves in this direction, it first becomes visible in the low-dimensional world as a cube, then changes its color until it finally returns disappears without seeming to move. The movement along the higher dimension is only visible as a change in the sectional image and not as a change in coordinates.
Physically widespread understanding
According to the mathematical definition above, a four-dimensional coordinate system is a coordinate system with four linearly independent directions. This is suitable for depicting our known three spatial dimensions and the time dimension.
In Einstein's theory of relativity , space and time are combined into a four-dimensional space - time . The space at a certain point in time is simply a hypersurface (in special relativity a hyperplane) in spacetime. Mathematically, the projection of space-time onto an ordinary three-dimensional space is comparable to the cutting planes of a cube (projection from 3D to 2D ). The “direction” of space (and time) in spacetime is not clearly determined. Indeed, the choice of space hyperplane depends on the frame of reference. This can be clearly illustrated in Minkowski diagrams , more information can also be found under Minkowski room .
However, spacetime - even the uncurved one - is not Euclidean , since a distance between two points of the flat spacetime is not defined by the usual vector norm, but by:
From the negative square it follows that the distances in time must have imaginary values.
For topological reasons, no fourth spatial dimension is required for embedding a curved 3D space.
The 3-D space can also be understood as 4- D space or space of even higher dimensions through any other dimension than time. This can be achieved through an additional scalar property, such as 1D, or a scale such as a color scale . This can e.g. B. with objects also the material property of temperature, mass or charge, or the spatial property of gravitational potential etc.
Cosmological meaning
Our learned imagination allows three-dimensional space. What is the real expansion of the space surrounding us in further directions is the object of investigation in cosmology .
4-dimensional bodies
- Tesseract , a four-dimensional hypercube , related to the three-dimensional cube
- Pentachoron , a four-dimensional hyperpyramid , related to the three-dimensional tetrahedron
- the four-dimensional hypersphere (see also unit sphere ), related to the three-dimensional sphere
- the four-dimensional cross polytope , related to the three-dimensional octahedron
4D flight guidance
Technology that not only organizes air traffic - in the air - predominantly in space, but also coordinates it over time, including airspeed and descent. Pilots and computers then no longer just act as separation managers, but as traffic flow managers in order to process dense air traffic more punctually and - thanks, for example, to fewer holding patterns - more energy-efficiently. On the occasion of a test in February 2012, a broad introduction is not promised before 2018.
Web links
- http://www.4d-screen.de/related-space - rotating bodies in hyperspace - z. B. 4d-plane, kleins bottle and hypercube
- http://www.dimensions-math.org/ Multilingual explanations and videos on the subject.
Individual evidence
- ↑ http://orf.at/stories/2113583/2108622/ Departure in the fourth dimension, ORF.at from April 4, 2012