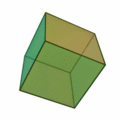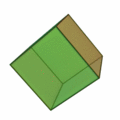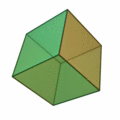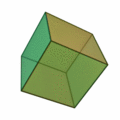
Cube (geometry)
| cube | |
|---|---|
|
|
| Type of side surfaces | Squares |
| Number of faces | 6th |
| Number of corners | 8th |
| Number of edges | 12 |
| Schläfli icon | {4.3} |
| dual to | octahedron |
| Body net |

|
| Number of different networks | 11 |
| Number of edges in a corner | 3 |
| Number of corners of a surface | 4th |
The cube (of German throw because he is thrown into dice games; also regular hexahedron [ hɛksaeːdər ], from the Greek. Hexáedron , hexahedron ', or cube , of ancient Greek κύβος kybos or lat. Cubus , cube') is one of the five Platonic Body , more precisely a three-dimensional polyhedron ( polyhedron ) with
- 6 congruent squares as side faces
- 12 edges of equal length and
- 8 corners , in each of which three sides meet.
The cube is a special three-dimensional parallelepiped , a special, namely equilateral cuboid and a special straight square prism . The sizes of a cube are already determined by specifying a value, edge length, surface diagonal, spatial diagonal, surface area or volume .
symmetry

with examples of the axes of rotation and the mirror planes (red and green)
Because of its high symmetry - all corners , edges and sides are similar to each other - the cube is a regular polyhedron . He has
- 3 fourfold axes of rotation (through the centers of two opposing surfaces ),
- 4 threefold axes of rotation (through two diagonally opposite corners),
- 6 twofold axes of rotation (through the centers of two diagonally opposite edges),
- 9 mirror levels (6 levels through four corners each (e.g. green), 3 levels through four edge centers each (e.g. red)),
- 14 rotations (6 by 90 ° with the planes through four edge centers each and 8 by 60 ° with planes through each six edge centers)
and is
- point symmetrical to the center M.
For a fourfold axis of rotation there are 3 symmetry operations ( rotation by 90 °, 180 ° and 270 °), for a threefold axis of rotation there are accordingly 2 symmetry operations. In total, the symmetry group of the cube has 48 elements. They are called in Schoenflies' notation as , in Hermann / Mauguin notation as, or in general, but somewhat imprecisely, as octahedron groups or cube groups.
Relations with other polyhedra
The cube is the dual polyhedron to the octahedron and vice versa. In addition, the corner points of the cube describe two point-symmetrical regular tetrahedra , which together form the star tetrahedron as another regular polyhedron .
With the help of cube and octahedron, numerous bodies can be constructed that also have the cube group as a symmetry group . So you get for example
- the truncated hexahedron or the truncated cube with 6 octagons and 8 triangles
- the cuboctahedron with 6 squares and 8 triangles, i.e. 14 sides, and 12 corners
- the truncated octahedron or the truncated octahedron with 6 squares and 8 hexagons
as the intersection of a cube with an octahedron (see Archimedean solids ) and
- the rhombic dodecahedron with 6 + 8 = 14 corners and 12 lozenges as sides
as a convex hull of a union of a cube with an octahedron.
The cube is a component of the regular cube tiling .
Formulas
| Sizes of a cube with edge length a | ||
|---|---|---|
| volume |
|
|
| Outer surface | ||
| Surface area | ||
| Umkugelradius | ||
| Edge ball radius | ||
| Inc sphere radius | ||
| Room diagonal | ||
| Surface diagonal | ||
|
Ratio of volume to spherical volume |
||
|
Angle between adjacent faces / edges |
||
| Solid angles in the corners | ||
Solid angles in the corners
This solid angle results very easily from considering the following situation.
For the three-dimensional space a is Cartesian coordinate system is used, the space in 8 octant divides. The 0-point of the three coordinate planes (x, y, z) is the meeting point of 8 virtual cubes. With the 0-point as the center of the unit sphere , the solid angle (full angle) has the value Considering, its solid angle is thus from 0 point, starting only 1 dice formed and to a unit referred to applies
generalization
The analogues of the cube in any dimension are also known as -dimensional cubes or hypercubes and are also regular polytopes . The -dimensional cube has limiting sides of dimension k. Special cases:
- The zero-dimensional cube ( point ) has 1 corner .
- The one-dimensional cube ( segment ) has 2 corners.
- The two-dimensional cube ( square ) has 4 corners and 4 edges
- The four-dimensional hypercube ( tesseract ) has 16 corners, 32 edges, 24 side squares and 8 side cubes.
- The n -dimensional cube has corners (k = 0), edges (k = 1), surfaces (k = 2), volumes (k = 3) and (n-1) -dimensional cubes as (k = n - 1) -dimensional pages ( facets ).
A model for the -dimensional cube is the unit cube in vector space . And that is the completed unit cube
- , the -fold Cartesian product of the unit interval
- the convex hull of the corner points with the coordinates and
- the intersection of the half-spaces and
The unit cube is an axis-parallel cube with the edge length and a corner in the origin of the coordinates . A generalization of this concept are cuboids im , which play a role in multidimensional analysis .
Networks of the cube
The cube has eleven nets (see illustration). These are certain hexominos . That means, there are eleven ways to unfold a hollow cube by cutting open 7 edges and spreading it out in the plane . The other 5 edges each connect the 6 squares of the network. To color a cube so that no neighboring faces are the same color, you need at least 3 colors.

Graphs, dual graphs, cycles, colors
The cube has an undirected planar graph with 8 nodes , 12 edges and 6 regions assigned to it, which is 3- regular , that is, 3 edges start from each node, so that the degree is 3 for all nodes. In the case of planar graphs, the exact geometric arrangement of the nodes is not important. However, it is important that the edges do not have to intersect. The nodes of this cube graph correspond to the corners of the cube.
The nodes of the cube graph can be colored with 2 colors so that neighboring nodes are always colored differently. In this alternate node coloring the color changes back and forth, if from one node to an adjacent is gone. This means that the chromatic number of this graph is 2. In addition, the edges can be colored with 3 colors so that neighboring edges are always colored differently (see illustration). This is not possible with 2 colors, so that the chromatic index for the edge coloring is 3 (the picture on the right illustrates this coloring).
The dual graph (octad graph ) with 6 nodes , 12 edges and 8 areas is helpful to determine the required number of colors for the areas or areas . The nodes of this graph are assigned one-to-one (bijective) to the areas of the cube graph and vice versa (see bijective function and figure above). The nodes of the octader graph can be colored with 3 colors so that neighboring nodes are always colored differently, but not with 2 colors, so that the chromatic number of the octad graph is 3. From this one can indirectly conclude: Because the chromatic number is equal to 3, 3 colors are necessary for such a surface coloring of the cube or a coloring of the areas of the cube graph.


The 7 cut edges of each network (see above) together with the corners ( nodes ) form a spanning tree of the cube graph . Each net corresponds exactly to a spanning tree and vice versa, so that there is a one-to-one ( bijective ) assignment between nets and spanning trees. If you consider a cube network without the outer area as a graph, you get a dual graph with a tree with 6 nodes and 5 edges and the maximum node degree 4. Each area of the cube is assigned to a node of the tree. Every graph-theoretic constellation (see isomorphism of graphs ) of such trees occurs, some also several times.
The cube graph has 12 Hamilton circles , but no Euler circles .
Cut surfaces of the cube
If a cube is cut from a plane, the cut surface can be a triangle , square , (irregular) pentagon or hexagon . An equilateral triangle , a square or a regular hexagon is also possible as a cut surface .
A cut surface in the form of a regular pentagon - no parallel sides - is not feasible, since two surfaces are parallel to each other in the cube.
Room fills with cubes
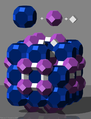
The three-dimensional Euclidean space can be completely filled with Platonic solids or in combination with Archimedean solids (and prisms ) of the same edge length. Such three-dimensional tiling is called room filling . The following room fills contain cubes:
Room filling with rhombic cuboctahedron , cuboctahedron and cube
Room filling with rhombic cuboctahedron, cube and tetrahedron
Room filling with truncated hexahedron , rhombic cuboctahedron, octagonal prism and cube
Room filling with large rhombic cuboctahedron , truncated octahedron and cube
Craftsmanship
Inserted cube
Over a hundred matches can be used to make cubes that hold together simply by clamping and friction.
origami
With the help of the origami technique, a cube can be made from individual sheets of paper without using glue.
Lathe
A cube can also be produced in a 3-jaw chuck on a lathe for metal cutting using a 4-jaw chuck or a gentle tubular holder. Turning a combination of up to four loose, but captive dice, one inside the other is a task of skill . This workpiece is called the turner's cube in English . The three outer cubes have a large hole in each side, which, as a window, allows a view of the next one or the next on the inside. The sizes of the three inner cubes are graded in such a way that the diagonal of the surface does not fit through this hole in the next larger one. It is necessary to undercut each side of the inner cubes and temporarily fix them with glue or wax if the sixth sides are to be worked on last.
See also
Web links
- Euclid: Stoicheia. Book XIII.15. Cube of a sphere
- Representation of oblique images, central projections, networks and sections of cubes
- Puzzle for the spatial conception of cubes
- interactive representation of multidimensional cubes
Individual evidence
- ^ Wolfram Demonstrations Project: All 11 Folding Nets of the Cube
- ↑ C. Dalfó, MA Fiol: Graphs, Friends and Acquaintances. (PDF) 2 Shaking hands: Colorings and Boolean algebra. Universitat Politècnica de Catalunya, Departament de Matemàtica Aplicada IV, 2010, p. 5 , accessed on May 31, 2020 .
- ↑ Richard Goldstone, Robert Suzzi Valli: Unfoldings of the cube . In: The College Mathematics Journal . tape 50 , no. 3 , May 28, 2019, ISSN 0746-8342 , p. 173-184 , doi : 10.1080 / 07468342.2019.1580108 ( researchgate.net [PDF]).
- ^ Wolfram Math World: Cubical Graph
- ↑ themetalcutter: Cube in a cube / Turners cube youtube.com, video (43:07) from August 19, 2015, accessed on March 17, 2017.




































![I ^ {n} = [0.1] \ times \ cdots \ times [0.1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/62fa17f870540204d44b501791c78c5cadd0f77f)