Platonic solid

The five platonic solids as art objects in the Bagno Steinfurt

The five platonic solids with motifs by MC Escher

The Platonic solids (after the Greek philosopher Plato ) are the polyhedra with the greatest possible symmetry . Each of them is bounded by several congruent ( congruent ) plane regular polygons . Another name is regular bodies (from Latin corpora regularia ).

There are five platonic solids. Their names contain the Greek expressed number of their bounding surfaces and eder as a modification of the Greek word ἕδρα ( hedra ) (see also polyhedron ), German (seat) surface.

• Tetrahedron (quadruple, surface made up of four triangles)
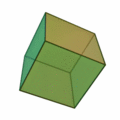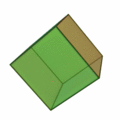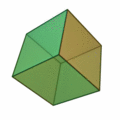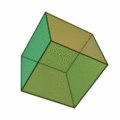
• Hexahedron (hexahedron, surface of six squares) - of the dice
• Octahedron (octahedron, surface of eight triangles)
• Dodecahedron (dodecahedron, surface from twelve pentagons) - also pentagonal dodecahedron called to indicate to the surface of pentagons as his special
• Icosahedron (twenty surfaces, surface of twenty triangles)

The Platonic solids are convex . In each corner of the body the same number of edges of the same length meet, at each edge two congruent surfaces meet, and each surface has the same number of corners. So it is not possible to distinguish any two body corners, edges and surfaces from one another based on relationships to other points of the polyhedron.

Alternatively, the Platonic solids can be defined as those polyhedrons , for which there is any pair of side surfaces , edges or corners is always a symmetry figure interchanged these surfaces, edges or corners. This is meant with the greatest possible symmetry .

If one renounces the indistinguishability of the surfaces and edges, one speaks of Archimedean solids . If, on the other hand, the indistinguishability of the corners and edges is omitted, one speaks of Catalan bodies . If one does not use convexity, one speaks of regular polyhedra and includes the Kepler-Poinsot solids .

Overview

The five platonic solids	Tetrahedron	Hexahedron	octahedron	Dodecahedron	Icosahedron
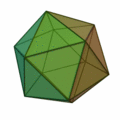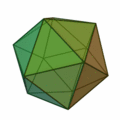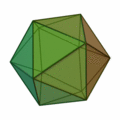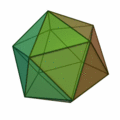
Type of side surfaces	equilateral triangles	Squares	equilateral triangles	regular pentagons	equilateral triangles
Number of corners / edges of a surface	3	4th	3	5	3
Number of faces / edges in a corner	3	3	4th	3	5
Number of corners	4th	8th	6th	20th	12
Number of edges	6th	12	12	30th	30th
Number of faces	4th	6th	8th	12	20th
Body net , the figures each show an example from several possible nets
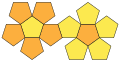
Number of different body networks	2	11	11	43380	43380
dual to	Tetrahedron	octahedron	Hexahedron	Icosahedron	Dodecahedron
Schläfli icon	{3.3}	{4.3}	{3.4}	{5.3}	{3.5}

properties

The following list contains a comprehensive description of the properties of the Platonic solids:

• The surface is made up of surfaces , they are polyhedra .
• They are convex : there are no re-entrant corners or edges.
• All edges are the same length.
• All surfaces are congruent with one another : They can be converted into one another by rotating and shifting.
• All corners have the same surface angle and edge angle , all surfaces are equilateral and equiangular .
• All corners have the same distance from the center of the body .
• There is an umkugel , an edge ball and an incugel .

Shapes of body corners

The condition that only identical polygons meet at a body corner is only fulfilled by five shapes of corners . The proof of this can already be found in Euclid . It is based on the following considerations:

• For any corner of the body, the sum of the interior angles of all adjoining surfaces is less than 360 °. If it were exactly 360 °, the surfaces would lie in one plane . Even with more than 360 °, no corner would be possible.
• On the other hand, at least three surfaces must meet at each corner of the body .

If all side surfaces of a body are equilateral triangles ( interior angle 60 °), three, four or five equilateral triangles ( angle sum 180 °, 240 °, 300 °) can meet at one corner .

If the side surfaces are squares ( interior angle 90 °) or regular pentagons (interior angle 108 °), three of them can meet ( sum of angles 270 ° for squares or 324 ° for pentagons).

The sum of the interior angles of 6 equilateral triangles , 4 squares , 4 regular pentagons or 3 regular hexagons is already 360 ° or larger. The 360 ° sum of the internal angles of six equilateral triangles, four squares and three regular hexagons means that no area in the space is created, but a regular tiling of the plane will take place (see section Platonic solids than regular tilings of the sphere ). If the sum of interior angles is greater than 360 °, corresponding polygons cannot meet in just one common corner at all.

Polygon	Interior angle	Polygons per corner and corner sum angle / polyhedron with such corners
		3	4th	5	6th	≥ 7
Equilateral triangle	60 °	180 ° / tetrahedron	240 ° / octahedron	300 ° / icosahedron	360 °	> 360 °
square	90 °	270 ° / hexahedron	360 °	> 360 °	> 360 °	> 360 °
Regular pentagon	108 °	324 ° / dodecahedron	> 360 °	> 360 °	> 360 °	> 360 °
Regular hexagon	120 °	360 °	> 360 °	> 360 °	> 360 °	> 360 °
Seven or more corners	128.57 degrees or greater	> 360 °	> 360 °	> 360 °	> 360 °	> 360 °

duality

For each convex polyhedron , a can dual body design. In the case of Platonic solids, this is obtained by connecting the midpoints of adjacent side faces with one another. Dual bodies in the narrower sense have the same edge sphere . Corresponding edges of the dual bodies intersect at a right angle at the point where they touch the edge sphere.

Thus, the dual polyhedron has as many corners as the starting polyhedron has faces . The dual body also has as many surfaces as the original body has corners. The latter can be imagined spatially in such a way that each enlarged area of ​​the dual body cuts off a corner of the original body. Third, the dual polyhedron and its starting polyhedron have the same number of edges. This can also be seen from the above construction: Two adjacent side surfaces together form an edge of the starting polyhedron, and the “connection of the two centers” of these adjacent side surfaces represents an edge of the dual body. This is why one speaks of dimension-reversing duality . And the inversion of the Schläfli symbol provides the dual polyhedron.

In the case of the Platonic solids, as a subgroup of the convex polyhedra , there are also the following special features with regard to their dual solids : First, the starting and dual solids have the same geometric center of gravity . Second, the dual field of a platonic field is also a platonic field itself. The hexahedron ( cube ) and octahedron as well as the dodecahedron and icosahedron each form a dual pair. The tetrahedron is dual to itself, but the dual tetrahedron is in a reduced, centrally symmetric position, i.e. that is, it is "upside down". Thirdly: If you repeat the above construction and construct the dual body to form a dual body, you get a scaled-down initial body - i.e. a Platonic body that can be converted into the initial body by centric stretching . Both have the same focus .

• 

  Two interlocking dual tetrahedra that form a star tetrahedron

• 

  Nested hexahedron ( cube ) and octahedron , which are dual to each other

• 

  Nested dodecahedron and icosahedron that are dual to each other

symmetry

The platonic solids show the greatest possible symmetry :

• Corners, edges and surfaces are similar to one another, i. That is, every corner (edge, surface) can be mapped to every other corner (edge, surface) by means of a congruence mapping of the body.

They say:

• The symmetry group acts transitively on the corners (as well as on the edges and surfaces).

It even applies:

• The symmetry group acts transitively on the flags . (A flag is a corner on an edge on a surface.)

The five platonic solids are therefore regular polyhedra . The symmetry groups occurring in them and their subgroups belong to the discrete point groups . Dual platonic solids have the same symmetry group . This is the basis for the construction of numerous other bodies, e.g. B. the Archimedean body . So there are not five, but only three of these groups: the tetrahedral group , the cube group and the icosahedral group . They play a role in mathematics in different contexts.

Due to their symmetry , homogeneously manufactured models of Platonic solids have the property that they can fall on each of their surfaces with exactly the same probability when thrown . By the way, most dice are not perfectly symmetrical due to the depressions for the numbers.

Deltaeder

Since the tetrahedron , octahedron and icosahedron also belong to the convex deltahedra , a body from every symmetry group belongs to the deltahedra.

Touching balls

From the high symmetry it follows immediately: Every platonic solid has

• an inc sphere that touches all of its surfaces , and
• a sphere on which all its corners lie, as well as
• an edge sphere on which the midpoints of the edges lie.

The common center of these three spheres is the center of the Platonic solid.

Mathematical properties

Platonic solids as regular tiling of the sphere

See also : Platonic tiling

If you project the edges of a Platonic solid from the center onto a sphere with the same center, e.g. B. on the sphere, the surface of the sphere is tiled by regular spherical polygons congruent to one another, with the same number of edges meeting at the same angles in each corner. These tiling have the same symmetries as the original body. In particular, they are also flag transitory . It is the five regular tiling of the sphere, between which the same duality relationships exist as between the bodies. In another context, one also speaks of maps and dual maps .

Every regular tiling can be described by a pair , the so-called Schläfli symbol, where stands for the number of edges of a field and the number of edges ending in a corner . The Platonic solids are the dual pairs ( hexahedron ) and ( octahedron ), ( dodecahedron ) and ( icosahedron ) as well as the self- dual ( tetrahedron ). ${\displaystyle \{p,q\}}$ ${\displaystyle p}$ ${\displaystyle q}$ ${\displaystyle \{4,3\}}$ ${\displaystyle \{3,4\}}$ ${\displaystyle \{5,3\}}$ ${\displaystyle \{3,5\}}$ ${\displaystyle \{3,3\}}$

Geometrically, this means for the platonic solids that

• ${\displaystyle p}$is the number of corners of the side faces . The sides of the platonic solid are therefore regular corners. ${\displaystyle p}$
• ${\displaystyle q}$are the number of faces / edges of the platonic solid that meet at a corner.

The sum of the interior angles at a corner of the Platonic solid is therefore (see Regular Polygon - Angle ). This results in the inequality ${\displaystyle q\cdot {\tfrac {p-2}{p}}\cdot 180^{\circ }}$

${\displaystyle {\begin{aligned}q\cdot {\tfrac {p-2}{p}}\cdot 180^{\circ }&<360^{\circ }\Rightarrow \\{\frac {1}{p}}+{\frac {1}{q}}&>{\frac {1}{2}}\left(p,q\in \mathbb {N} \right)\end{aligned}}}$

with the above solutions . This relationship also follows from Euler's theorem of polyhedra , which relates the number of corners, edges and surfaces to one another: ${\displaystyle E}$ ${\displaystyle K}$ ${\displaystyle F}$

${\displaystyle E-K+F=2}$,

where the constant 2 is characteristic of the sphere .

In Euclidean geometry applies to infinitely large planar graphs with a suitable, namely asymptotic interpretation of the equation

${\displaystyle E-K+F=0}$

or

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}\left(p,q\in \mathbb {N} \right)}$

with the solutions

${\displaystyle \{4,4\}}$(self- dual ) as well as and dual to it , which stand for the three Platonic tiling of the plane (by squares , equilateral triangles and regular hexagons ), which represent generalizations of the Platonic solids. ${\displaystyle \{3,6\}}$ ${\displaystyle \{6,3\}}$

The solutions from

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}\ (p,q\in \mathbb {N} )}$

provide the regular tiling of the hyperbolic geometry .

For the platonic solids it is not only true , but also . This exclusively integer system of equations made up of three equations can be solved and results in the number of corners, edges and surfaces: ${\displaystyle E-K+F=2}$ ${\displaystyle p\cdot E=2\cdot K=q\cdot F}$ ${\displaystyle E}$ ${\displaystyle K}$ ${\displaystyle F}$

${\displaystyle E={\frac {4\cdot p}{4-(p-2)\cdot (q-2)}}}$

${\displaystyle K={\frac {2\cdot p\cdot q}{4-(p-2)\cdot (q-2)}}}$

${\displaystyle F={\frac {4\cdot q}{4-(p-2)\cdot (q-2)}}}$

For every Platonic solid, the number of corners, edges and surfaces can only be calculated by specifying and (see above), without knowing the exact geometric properties. ${\displaystyle p}$ ${\displaystyle q}$

Overview

General considerations the platonic solids	General case	Tetrahedron	Hexahedron	octahedron	Dodecahedron	Icosahedron
Schläfli icon	${\displaystyle \{p,q\}}$	{3.3}	{4.3}	{3.4}	{5.3}	{3.5}
Number of corners	${\displaystyle E={\frac {4\cdot p}{4-(p-2)\cdot (q-2)}}}$	4th	8th	6th	20th	12
Number of edges	${\displaystyle K={\frac {2\cdot p\cdot q}{4-(p-2)\cdot (q-2)}}}$	6th	12	12	30th	30th
Number of faces	${\displaystyle F={\frac {4\cdot q}{4-(p-2)\cdot (q-2)}}}$	4th	6th	8th	12	20th
Inner angles of the side surfaces	${\displaystyle \alpha ={\tfrac {p-2}{p}}\cdot 180^{\circ }}$	60 °	90 °	60 °	108 °	60 °
Sum of the interior angles	${\displaystyle q\cdot {\tfrac {p-2}{p}}\cdot 180^{\circ }}$	180 °	270 °	240 °	324 °	300 °
Angular defect (360 ° - sum of the interior angles )	${\displaystyle (2-q\cdot {\tfrac {p-2}{p}})\cdot 180^{\circ }}$	180 °	90 °	120 °	36 °	60 °

Surface area

For the area of the surface of the Platonic solid, the side length and the Schläfli symbol apply ${\displaystyle a}$ ${\displaystyle \{p,q\}}$

${\displaystyle A_{O}={\frac {p\cdot q\cdot a^{2}}{4-(p-2)\cdot (q-2)}}\cdot \cot \left({\frac {\pi }{p}}\right)}$

because the surface is composed of congruent regular - corners (see Regular Polygon - the size and surface area ) ${\displaystyle F={\tfrac {4\cdot q}{4-(p-2)\cdot (q-2)}}}$ ${\displaystyle p}$

Angle between adjacent faces

The following applies to the angle between adjacent surfaces ( dihedral angle ) ${\displaystyle \beta }$

${\displaystyle \beta =2\cdot \arcsin \left({\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}\right)\Leftrightarrow \sin \left({\frac {\beta }{2}}\right)={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}}$

because of , because the platonic solids are convex. ${\displaystyle 0<\beta <\pi }$

For this it is sufficient to consider a diagonal (see Regular polygon - diagonals ) of the regular - corner , which is stretched out like an umbrella by the corners of the edges that meet at a certain corner , and the two equally long heights of the end points (corners ) of this diagonal onto the edge that connects the corner under consideration with the corner jumped over by the diagonal . On this isosceles triangle can Sinus be applied. ${\displaystyle d_{2}}$ ${\displaystyle q}$ ${\displaystyle d_{2}}$

The sides of this regular - gon ( "Umbrella"), the diagonals of the lateral surfaces of the Platonic solid, ie the regular -Ecke the side length a, which meet at the relevant corner. You have the length ${\displaystyle q}$ ${\displaystyle d_{2}}$ ${\displaystyle p}$

${\displaystyle {\frac {a\cdot \sin \left({\frac {2\cdot \pi }{q}}\right)}{\sin \left({\frac {\pi }{q}}\right)}}=2\cdot a\cdot \cos \left({\frac {\pi }{q}}\right)}$

Umkugelradius, edge ball radius, incugelradius

From this angle between adjacent surfaces of the blank Umkugelradius , edge radius of the sphere and the Inkugelradius of Platonic solid determine by the addition circumradius and Inkreisradius the affected side surface , a regular - Eck is considered (see Regular Polygon - circle as a boundary form ): ${\displaystyle \beta }$ ${\displaystyle r_{u}}$ ${\displaystyle r_{k}}$ ${\displaystyle r_{i}}$ ${\displaystyle p}$

${\displaystyle r_{u}={\frac {a}{2}}\cdot \tan \left({\frac {\pi }{q}}\right)\cdot \tan \left({\frac {\beta }{2}}\right)}$

${\displaystyle r_{k}={\frac {a}{2}}\cdot {\frac {\cos \left({\frac {\pi }{p}}\right)}{\cos \left({\frac {\pi }{q}}\right)}}\cdot \tan \left({\frac {\beta }{2}}\right)}$

${\displaystyle r_{i}={\frac {a}{2}}\cdot \cot \left({\frac {\pi }{p}}\right)\cdot \tan \left({\frac {\beta }{2}}\right)}$

Solid angles in the corners

In 2015 HC Rajpoot published a simple formula for the corner solid angle

${\displaystyle \Omega =2\pi -2n\cdot \arcsin \left(\cos \left({\frac {\pi }{n}}\right)\cdot {\sqrt {\tan ^{2}\left({\frac {\pi }{n}}\right)-\tan ^{2}\left({\frac {\alpha }{2}}\right)}}\right),}$

which is used in all five platonic solids. Herein the two mean variables

• ${\displaystyle n}$ the number of edges / surfaces that meet at a corner of the platonic solid, i.e. for

	Tetrahedron, cube and dodecahedron	${\displaystyle n=3}$ ,
	octahedron	${\displaystyle n=4}$ and for
	Icosahedron	${\displaystyle n=5}$ ;

• and the interior angle of a surface of the Platonic field, i.e. for ${\displaystyle \alpha }$

	Tetrahedron, octahedron and icosahedron	${\displaystyle \alpha =60^{\circ }=\pi /3}$ ,
	cube	${\displaystyle \alpha =90^{\circ }=\pi /2}$ and for
	Dodecahedron	${\displaystyle \alpha =108^{\circ }=3\pi /5}$ .

volume

From the surface and the Inkugelradius eventually resulting volume , because every platonic solids can be divided into regular pyramids decompose the one side surface , so regular - Eck , as base and Inkugelradius as height have: ${\displaystyle F={\tfrac {4\cdot q}{4-(p-2)\cdot (q-2)}}}$ ${\displaystyle p}$

${\displaystyle {\begin{aligned}V&={\frac {1}{3}}\cdot A\cdot r_{i}={\frac {1}{3}}\cdot {\frac {p\cdot q\cdot a^{2}}{4-(p-2)\cdot (q-2)}}\cdot \cot \left({\frac {\pi }{p}}\right)\cdot {\frac {a}{2}}\cdot \cot \left({\frac {\pi }{p}}\right)\cdot \tan \left({\frac {\beta }{2}}\right)\\&={\frac {p\cdot q\cdot a^{3}}{24-6\cdot (p-2)\cdot (q-2)}}\cdot \cot ^{2}\left({\frac {\pi }{p}}\right)\cdot \tan \left({\frac {\beta }{2}}\right)\end{aligned}}}$

Formulas

Sizes of a Platonic field with p corners / edges per surface, q surfaces / edges in a corner and edge length a
	General case	Example dodecahedron
Schläfli icon	${\displaystyle \{p,q\}}$	${\displaystyle \{5,3\}}$
volume	${\displaystyle V={\frac {p\cdot q\cdot a^{3}}{24-6\cdot (p-2)\cdot (q-2)}}\cdot \cot ^{2}\left({\frac {\pi }{p}}\right)\cdot \tan \left({\frac {\beta }{2}}\right)}$	${\displaystyle V\approx 7{,}663\cdot a^{3}}$
Surface area	${\displaystyle A_{O}={\frac {p\cdot q\cdot a^{2}}{4-(p-2)\cdot (q-2)}}\cdot \cot \left({\frac {\pi }{p}}\right)}$	${\displaystyle A_{O}\approx 20{,}646\cdot a^{2}}$
Umkugelradius	${\displaystyle r_{u}={\frac {a}{2}}\cdot \tan \left({\frac {\pi }{q}}\right)\cdot \tan \left({\frac {\beta }{2}}\right)}$	${\displaystyle r_{u}\approx 1{,}401\cdot a}$
Edge ball radius	${\displaystyle r_{k}={\frac {a}{2}}\cdot {\frac {\cos \left({\frac {\pi }{p}}\right)}{\cos \left({\frac {\pi }{q}}\right)}}\cdot \tan \left({\frac {\beta }{2}}\right)}$	${\displaystyle r_{k}\approx 1{,}309\cdot a}$
Inc sphere radius	${\displaystyle r_{i}={\frac {a}{2}}\cdot \cot \left({\frac {\pi }{p}}\right)\cdot \tan \left({\frac {\beta }{2}}\right)}$	${\displaystyle r_{i}\approx 1{,}114\cdot a}$
Ratio of the radius of the sphere to Umkugelradius	${\displaystyle {\frac {r_{i}}{r_{u}}}=\cot \left({\frac {\pi }{p}}\right)\cdot \cot \left({\frac {\pi }{q}}\right)}$	${\displaystyle {\frac {r_{i}}{r_{u}}}\approx 0{,}795}$
Ratio of volume to umkugelvol	${\displaystyle {\frac {V}{V_{UK}}}={\frac {1}{\pi }}\cdot {\frac {p\cdot q\cdot a^{3}}{4-(p-2)\cdot (q-2)}}\cdot \cot ^{2}\left({\frac {\pi }{p}}\right)\cdot \cot ^{3}\left({\frac {\pi }{q}}\right)\cdot \cot ^{2}\left({\frac {\beta }{2}}\right)}$	${\displaystyle {\frac {V}{V_{UK}}}\approx 0{,}665}$
Ratio of spherical volume to volume	${\displaystyle {\frac {V_{IK}}{V}}=\pi \cdot {\frac {4-(p-2)\cdot (q-2)}{p\cdot q\cdot a^{3}}}\cdot \cot \left({\frac {\pi }{p}}\right)\cdot \tan ^{2}\left({\frac {\beta }{2}}\right)}$	${\displaystyle {\frac {V_{IK}}{V}}\approx 0{,}755}$
Inner angle of the side surface ( regular - corner ) ${\displaystyle p}$	${\displaystyle \left(1-{\frac {2}{q}}\right)\cdot 180^{\circ }}$	${\displaystyle \alpha =108^{\circ }}$
Angle between adjacent faces	${\displaystyle \beta =2\cdot \arcsin \left({\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}\right)}$	${\displaystyle \beta \approx 116^{\circ }\;33^{\prime }\;54^{\prime \prime }}$
Solid angles in the corners	${\displaystyle \Omega =2\cdot \pi -2\cdot p\cdot \arcsin \left(\cos \left({\frac {\pi }{p}}\right)\cdot {\sqrt {\tan ^{2}\left({\frac {\pi }{p}}\right)-\tan ^{2}\left(\left({\frac {1}{2}}-{\frac {1}{q}}\right)\cdot \pi \right)}}\right)}$	${\displaystyle \Omega \approx 2{,}962\;\mathrm {sr} }$

Note: The following applies to the angle between adjacent surfaces ( dihedral angle ) (see arctangent and arctangent ): ${\displaystyle \beta }$

${\displaystyle \tan \left({\frac {\beta }{2}}\right)=\tan \left(\arcsin \left({\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}\right)\right)=\left({\frac {\sin ^{2}\left({\frac {\pi }{p}}\right)}{\cos ^{2}\left({\frac {\pi }{q}}\right)}}-1\right)^{-{\frac {1}{2}}}}$because of and ${\displaystyle \tan(\arcsin(x))={\frac {x}{\sqrt {1-x^{2}}}}}$

${\displaystyle \cot \left({\frac {\beta }{2}}\right)=\cot \left(\arcsin \left({\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}\right)\right)=\left({\frac {\sin ^{2}\left({\frac {\pi }{p}}\right)}{\cos ^{2}\left({\frac {\pi }{q}}\right)}}-1\right)^{\frac {1}{2}}}$because of . ${\displaystyle \cot(\arcsin(x))={\frac {\sqrt {1-x^{2}}}{x}}}$

Platonic solids in platonic solids

Platonic solids can be inscribed in other Platonic solids, so that as many corners of the inner polyhedron as possible lie on the surface of the outer polyhedron. In some cases all corners, all edges, some edges or some faces of the inner polyhedron touch the surface of the outer polyhedron.

	Tetrahedron	Hexahedron	octahedron	Dodecahedron	Icosahedron
Tetrahedron
Hexahedron
octahedron
Dodecahedron
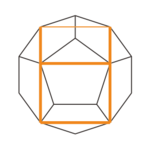
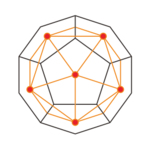
Icosahedron

Graph theoretical properties

All graphs of the Platonic solids are regular graphs because the same number of edges meet at each corner of these polyhedra . The shortest cycle , the so-called waist size , is equal to the number of corners of the side faces of the Platonic solid in question.

The graph-theoretical diameter and the graph-theoretical radius agree because all nodes are graph-theoretical equivalent to one another and can be mapped together with the graph on an isomorphic graph with the help of permutations . It follows that all nodes have the same eccentricity and belong to both the edge and the center of the graph.

Networks

Like all polyhedra, Platonic solids have different networks (see overview above). There are different ways to unfold a hollow polyhedron by cutting open some edges and spreading it out in the plane . If the number of edges and the number of faces of the polyhedron are, then a body mesh is created by cutting the edges. The corners are obviously on the edge of the net. The other edges connect the regular polygons of the network. ${\displaystyle K}$ ${\displaystyle F}$ ${\displaystyle K-F+1}$ ${\displaystyle F-1}$

Every Platonic solid, like every convex polyhedron, has an undirected planar graph assigned to it . This graph is regular is because of each node going edges, so that the degree for all nodes equal , where the number of nodes. The node degree is equal to the number of faces (and edges ) that meet in each corner of the Platonic solid. In the case of planar graphs, the exact geometric arrangement of the nodes is not important. However, it is important that the edges do not have to intersect. The nodes of this graph correspond to the corners of the polyhedron. ${\displaystyle {\tfrac {2\cdot K}{E}}}$ ${\displaystyle {\tfrac {2\cdot K}{E}}}$ ${\displaystyle E}$

The cut edges of each network together with the corners ( nodes ) form a spanning tree of the graph. Each net corresponds exactly to a spanning tree and vice versa, so that there is a one-to-one ( bijective ) assignment between nets and spanning trees. If you consider a body network without the outer area as a graph, you get a dual graph with a tree with nodes and edges and the maximum node degree . Each area of the platonic solid is assigned to a node of the tree. ${\displaystyle K-F+1}$ ${\displaystyle F}$ ${\displaystyle F-1}$ ${\displaystyle {\tfrac {2\cdot K}{F}}}$

These considerations are related to Euler's polyhedron substitution .

Dual graphs and colors

Edge coloring of the dodecahedron graph

Area coloring of the dodecahedron graph with dual node coloring of the icosahedron graph

The minimum number of colors that is required to color the nodes of a graph so that neighboring nodes are always colored differently is called the chromatic number (see node coloring ). The corresponding number for the edges is called the chromatic index (see edge coloring ). In the graphs of the Platonic solids it is equal to the (maximum) node degree. In connection with Vizing's theorem , they are called class 1 graphs .

The nodes of the icosahedral graph can be colored with 4 colors so that neighboring nodes are always colored differently. This means that the chromatic number of this graph is 4 (see node coloring ). In addition, the edges can be colored with 3 colors so that adjacent edges are always colored differently. This is not possible with 2 colors, so the chromatic index for the edge coloring is 3.

The dual graph is helpful in determining the corresponding number of colors required for the areas or areas . This graph-theoretical concept of duality is to a certain extent an analogy or generalization of the geometric duality of polyhedra (see section above ).

The nodes of this dual graph are uniquely (bijectively) assigned to the areas of the original graph and vice versa (see bijective function ). For the dodecahedron graph (see figures), for example, the following applies: The nodes of the dual icosahedron graph can be colored with 4 colors so that neighboring nodes are always colored differently, but not with 3 colors, so that the chromatic number of the icosahedron graph is 4. From this one can indirectly conclude: Because the chromatic number is equal to 4, 4 colors are necessary for such a surface coloring of the dodecahedron or a coloring of the areas of the dodecahedron graph.

Hamilton circles

Cube graph with Hamilton circle

All graphs of the Platonic solids have several Hamilton circles . This is a closed path in a graph that contains every node exactly once. With the cube and the dodecahedron this is anything but obvious. It is clear for the tetrahedron associated with the complete graph . For the octahedron the existence of Hamilton circles follows from a theorem by Gabriel Andrew Dirac , for the icosahedron from a theorem by William Thomas Tutte (see theorems about Hamilton circles ). ${\displaystyle K_{4}}$

However , there is no mathematical formula and no really simple algorithm for the number of Hamilton circles . Investigations with the computer show, for example, that the icosahedron has 2560 Hamilton circles.

Euler circles

The graphs of tetrahedron , cube , dodecahedron and icosahedron do not have Euler circles because the degrees of all nodes are odd. This is because an odd number of edges meet in each corner of these polyhedra . The octahedron has 1844 Euler circles, as studies with the computer show.

Overview

The five platonic solids	Tetrahedron	Hexahedron	octahedron	Dodecahedron	Icosahedron
polyhedron
associated regular graph
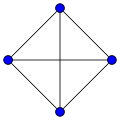
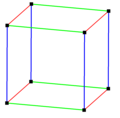
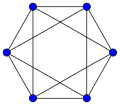
chromatic number (see node color )	4th	2	3	3	4th
chromatic index (see edge coloring )	3	3	4th	3	5
Number for area coloring (see dual graph )	4th	3	2	4th	3
Node degree (see regular graph )	3	3	4th	3	5
Node connection number	3	3	4th	3	5
Edge connection number	3	3	4th	3	5
shortest cycle ( waist size )	3	4th	3	5	3
graph theoretical diameter	1	3	2	5	3
graph-theoretical radius	1	3	2	5	3
Clique count	4th	2	3	2	3
Stability number	1	4th	2	8th	3
Number of Hamilton circles	6th	12	32	60	2560
Number of Euler circles	0	0	1488	0	0

Polyhedra derived from the platonic solids

See also : Derivations from the Platonic Solids

Because of the strong regularity of the platonic solids, it is easy to derive other solids from them that are again very regular. You just have to apply the same constructions symmetrically to surfaces , edges or corners . An example of this are the dual bodies that result from connecting the center of each surface with the center of the adjacent surfaces.

Truncated platonic solids

If you create a truncated polyhedron starting from a Platonic solid by cutting off its corners so that all edges are then the same length, you get an Archimedean solid . This body also arises as a section of the Platonic body with its suitably enlarged dual body.

• 

  Truncated tetrahedron

• 

  Truncated hexahedron

• 

  Truncated octahedron

• 

  Truncated dodecahedron

• 

  Truncated icosahedron (football body)

Archimedean solids are examples of fairly regular solids that use polygons that are regular but of different numbers of faces.

Star body

If you build pyramids on the side surfaces instead of cutting them off, you get star bodies like the star tetrahedron .

If one uses equilateral triangles for the pyramids , one has examples of polyhedra that consist entirely of the same polygons , but in which different numbers collide in the corners .

generalization

3D projection of the 24 cell

Flail diagram of the 24-cell cell

The Swiss mathematician Ludwig Schläfli determined the -dimensional relatives of the Platonic solids in 1852 - but his work went unnoticed for a long time. It turned out that in four-dimensional space there is a four-dimensional equivalent, a regular 4-polytope , to each of the five regular three-dimensional bodies (3-polytopes) : to the tetrahedron the 5-cell ( pentachoron ), to the cube the 8-cell ( Tesseract ), for the octahedron the 24-cell (Ikositetrachor) , for the dodecahedron the 120-cell ( Hekatonikosachor ) and for the icosahedron the 600-cell ( Hexakosichor ). Then there is a sixth regular 4-polytope: the 16-cell (Hexadekachor) . ${\displaystyle n}$

In the five-dimensional space - and also in all the rooms of higher dimension - there instead of five or six only three regular polytopes: as Simplex , the hyper tetrahedron , as Maßpolytop the hypercube and the cross-polytope its dual, the Hyperoktaeder .

history

Model of the solar system in Kepler's Mysterium Cosmographicum (1596)

earth

water

air

Fire

Ether / cosmos

Assignment of the Platonic solids to the elements in Kepler's Harmonice mundi

The Platonic Solids have been studied since ancient times . The Pythagoreans (6th century BC) distinguished at least between tetrahedron, hexahedron and dodecahedron. The octahedron may have been ignored because it was viewed as a double pyramid. The Athenians Theaetetus (415-369 v. Chr.) Also knew octahedron and icosahedron. He proved that there can only be five convex regular polyhedra.

The Greek philosopher Plato (approx. 427–347 BC), a contemporary of Theaetetus, was the namesake for the five bodies. In his work Timaeus (chap. 20, 53c4–55c6) he described them in detail. He incorporated the Platonic solids into his philosophical system by assigning them (with the exception of the dodecahedron) to the four elements (chap. 21, 55c7–56c7): fire stood for the tetrahedron, air for the octahedron. The icosahedron was associated with water , the hexahedron with earth . According to this theory, the dodecahedron could be equated with the fifth element, ether, postulated by Aristotle .

Euclid (360–280 BC) described the Platonic solids in the XIII. Book of its elements (§§ 13-17). In it he proved, among other things, that there are exactly five (§ 18a). Hypsikles took in the later added “XIV. Book ”(from the 2nd century BC) made some volume calculations. The “XV. Book “(6th century AD) contained further discoveries by Greek mathematicians regarding the five regular solids.

With the advent of perspective , several artists processed the platonic solids in their works: Piero della Francesca , Leonardo da Vinci (illustrations for Divina Proportione by Luca Pacioli ), Albrecht Dürer , Wenzel Jamnitzer ( Perspectiva Corporum Regularium , 1568).

Johannes Kepler succeeded ( Mysterium Cosmographicum , 1596) in depicting the orbital radii of the six planets known at the time using a certain sequence of the five bodies and their inner and outer spheres. This interpretation largely agreed with the astronomical values ​​known at the time, but actually did not correspond to any regularity.

Applications

The five platonic solids as dice

The striking regularity makes the platonic solids interesting for humans in many ways.

• Some Platonic solids are solutions to Thomson's problem (after Joseph John Thomson ): In graphic terms, this problem describes how n electrons are distributed on a spherical surface, so that the potential energy through their electric field is minimal.
• In addition to the classic, geometric cube, which is easy to manufacture and has been used for games of chance for thousands of years , the other platonic solids (also known as dice) are used in the game today, e.g. B. in pen & paper role-playing games (see dice ). The prerequisites for this are a physically even density distribution - i.e. homogeneous material - as well as the similar properties of all corners and edges.
• Platonic solids have long been objects of visual artists . In modern art , MC Escher in particular has dealt with them and regular bodies similar to them; Works by Salvador Dalí also address platonic solids or their development.
• Platonic polyhedra also play an important role in the adventure game The Dig .

The triangles of an icosahedron on which the protective shell of the Rasad-e Khan Observatory is based are shown in red.

• The purpose of the Roman pentagon dodecahedron is still speculated today.
• Rudolf von Laban concretized his spatial-rhythmic movement theory (choreography) mainly in the model of the icosahedron.
• In the management of teams, according to a suggestion by Stafford Beer , the platonic solids can be used as a model for networking when employees concentrate on their topics. Every employee corresponds to an edge, every topic to a corner of a platonic solid. For each topic, you meet regularly with precisely those employees whose edges converge in this topic corner. An employee works on a maximum of two topics at the same time and can concentrate well. Even with large teams (e.g. icosahedron = 30 employees, 5 employees per topic, 12 topics) this ensures that order is in place. Beer's idea was taken up at the Management Center in Sankt Gallen and a method based on it called Syntegrity was proposed.

Even in nature, existing regularities can be expressed as platonic solids.

Polyhedral forms, including the platonic solids of the radiolaria. Illustration by Ernst Haeckel (1834–1919).

• The arrangement of the hydrogen atoms, for example in the sp³-hybridized methane hybrid orbital, corresponds to a tetrahedron.
• Tetrahedra, cubes and octahedra occur naturally as (idealized) crystals ; dodecahedral and icosahedral symmetry elements can be found in quasicrystals .
• Exact dodecahedra do not appear as crystals. Crystals of certain minerals, such as B. Pyrite , which looks like a dodecahedron on the outside, are not exact pentagonal dodecahedra , but rather distorted. However, the distortion is often invisible to the naked eye from a distance. However, if you look up close, you can see that these bodies are not formed from regular (but irregular) pentagons. For example, sodium chloride and alum , which is doped with certain other substances when precipitated, form cube crystals. Pure alum crystallizes as an octahedron. The demarcation between the individual forms is not absolute, but the internal symmetry can express itself in different forms. In mineralogy, all the platonic solids tetrahedron, cube and octahedron as well as rhombic dodecahedron , cuboctahedron and their mixed forms fall under the term cubic . Quite a few minerals can accordingly assume several of these cubic forms. This includes, for example, pyrite, which occurs both as a cube and as an octahedron or, as described above, as a distorted dodecahedron.
• Platonic solids, especially the icosahedron , are very often structural forms as they are observed in clusters (i.e. small nanoparticles).
• Some of the platonic solids are made up of organic hydrocarbon molecules (see platonic hydrocarbons ).
• The dodecahedron is the smallest possible shape of the hollow carbon molecules known as fullerenes .
• The protein capsid of viruses can have different shapes, for example icosahedral.
• The calcareous skeletons of the radiolarians have very different shapes, including platonic solids.

literature

• Paul Adam, Arnold Wyss: Platonic and Archimedean solids, their star shapes and polar structures. Free Spiritual Life Publishing House, Stuttgart 1984, ISBN 3-7725-0965-7 .
• Renatus Ziegler: Platonic Solids. Relationships, metamorphoses, inversions. Verlag am Goetheanum, Dornach / Switzerland 2012, ISBN 978-3-7235-1326-2 .
• Ilka Agricola, Thomas Friedrich: Elementary Geometry. Expertise for studies and math lessons. Springer Spectrum, 4th edition 2015. ISBN 978-3-658-06730-4 , doi: 10.1007 / 978-3-658-06731-1 .

Web links

Commons : Platonic Solids  - Album with pictures, videos and audio files

Wikiversity: The Symmetry Groups of Platonic Solids  - Course Materials

Wiktionary: platonic solids  - explanations of meanings, word origins, synonyms, translations

• Euclid: Stoicheia. Book XIII.18. Edges of the five different polyhedra inscribed with spheres of the same diameter
• Craft sheets for platonic solids
• Learning environment Platonic Solids from the University of Bayreuth

Individual evidence

1. ^ Noua corpora regularia: seu, Quinque corporum regularium simplicium, in quinque alia regularia composita, metamorphosis. Inventa ante annos 60 à Thoma Diggseio Armigero, jam, prolematibus additis nonnullis, demonstrata à nepote
2. ↑ Christophorus Leibfried: Tabula III. Orbium Planetarum Dimensiones et Distantias Per Quinque Regularia Corpora Geometrica Exhibens
3. ^ ^{A b} Wolfram MathWorld: Regular Tetrahedron
4. ^ ^{A b} Wolfram MathWorld: Cube
5. ^ ^{A b} Wolfram MathWorld: Regular Octahedron
6. ↑ ^{a b} Wolfram MathWorld: Regular Dodecahedron
7. ^ ^{A b} Wolfram MathWorld: Regular Icosahedron
8. ^ Renatus Ziegler: Platonic bodies - relationships, metamorphoses, inversions. Dornach 2008, p. 10.
9. ↑ Euclid: The Elements. Book XIII, § 18a.
10. ↑ The number of surfaces is 2 times the number. of the edges divided by p , those of the corners 2 times the number. of the edges divided by q
11. ↑ Harish Chandra Rajpoot: Solid angles subtended by the platonic solids (regular polyhedra) at their vertices. SlideShare, March 2015, accessed June 16, 2020 . 
12. ↑ Eric Weisstein: Dodecahedron. Umkugelradius, formula (17) further simplified. In: MathWorld Wolfram. A Wolfram Web Resource, accessed July 1, 2020 . 
13. ↑ Eric Weisstein: Dodecahedron. Edge ball radius, formula (19). In: MathWorld Wolfram. A Wolfram Web Resource, accessed July 1, 2020 . 
14. ↑ Eric Weisstein: Dodecahedron. In spherical radius, formula (15). In: MathWorld Wolfram. A Wolfram Web Resource, accessed July 1, 2020 . 
15. ↑ Mike Zabrocki: HOMEWORK # 3 SOLUTIONS - MATH 3260. (PDF) York University, Mathematics and Statistics, Toronto, 2003, p. 4 , accessed May 31, 2020 . 
16. ^ Wolfram MathWorld: Tetrahedral Graph
17. ^ Wolfram MathWorld: Cubical Graph
18. ^ Wolfram MathWorld: Octahedral Graph
19. ^ Wolfram MathWorld: Dodecahedral Graph
20. ^ Wolfram MathWorld: Icosahedral Graph
21. ↑ Eric W. Weisstein : Platonic Solid . In: MathWorld (English).
22. ↑ Eric W. Weisstein : Pentachor . In: MathWorld (English).
23. ↑ Eric W. Weisstein : Tesseract . In: MathWorld (English).
24. ↑ Eric W. Weisstein : 24-cell . In: MathWorld (English)., Bounded by 24 (three-dimensional) octahedra, 96 triangular surfaces, 96 edges and 24 corners.
25. ↑ Eric W. Weisstein : 120-cell . In: MathWorld (English).
26. ↑ Eric W. Weisstein : 600-cell . In: MathWorld (English).
27. ↑ Eric W. Weisstein : 16-cell . In: MathWorld (English).
28. ↑ Oliver Knill, Math circle Northeastern, Harvard Mathematics Department Home page: Polyhedra and Polytopes
29. ↑ Martin Pfiffner: Team Syntegrity - The cybernetic path to decision-making in organizations . Malik on Management, 5/2001, pp. 82-95. Online under Archived Copy ( Memento from January 31, 2012 in the Internet Archive )