Cross polytop

An octahedron is a three-dimensional cross polytope

A cross polytope or hyperoctahedron is a polytope in geometry that represents a generalization of an octahedron from three-dimensional space to spaces of any dimension . A cross polytope in -dimensional space is the convex hull of lines which all intersect at a common intersection point. In the case of a regular cross polytop , these stretches are all the same length and each intersect centrally and at right angles . The symmetry group of a regular cross polytop is the hyperoctahedral group . Besides hypercubes and regular simplices , regular cross polytopes are the only regular polytopes that exist in any dimensions. Cross polytopes are used, among other things, in linear optimization . ${\displaystyle n}$ ${\displaystyle n}$

Unity cross polytop

Two-dimensional unit cross polytope with coordinate axes

definition

The -dimensional unit cross-polytope is the convex hull of the corners : ${\displaystyle n}$ ${\displaystyle 2n}$ ${\displaystyle \pm e_{1},\ldots ,\pm e_{n}}$

${\displaystyle P=\operatorname {conv} ({e_{1},\ldots ,e_{n},-e_{1},\ldots ,-e_{n}})\subseteq \mathbb {R} ^{n}}$.

Here denotes the -th unit vector of the vector space . ${\displaystyle e_{i}=(0,0,\ldots ,1,0,\dots 0)}$ ${\displaystyle i}$ ${\displaystyle \mathbb {R} ^{n}}$

Examples

• The one-dimensional unit cross polytope is the closed unit interval . ${\displaystyle [-1,1]}$
• The two-dimensional unit cross polytope is a square (turned upside down) .
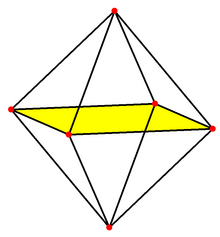
• The three-dimensional unit cross polytope is an octahedron and thus one of the Platonic solids .

presentation

The unit cross polytope can also be represented as a point set in -dimensional space as follows: ${\displaystyle n}$

${\displaystyle P=\{(v_{1},v_{2},\dotsc ,v_{n})\in \mathbb {R} ^{n}\mid |v_{1}|+|v_{2}|+\dotsb +|v_{n}|\leq 1\}}$.

The unit cross polytope is thus the unit sphere with regard to the sum norm . This absolute inequality can also be described as a system of linear inequalities. Therefore, the unit cross polytope is delimited by precisely hyperplanes . ${\displaystyle \|\cdot \|_{1}}$ ${\displaystyle 2^{n}}$ ${\displaystyle 2^{n}}$

Components

The unit cross polytope is convex , closed and connected (with respect to the Euclidean metric ). It consists of the following components:

• It has corners, just the (positive and negative) unit vectors. ${\displaystyle 2n}$
• It has edges because every corner , except the opposite corner, is connected to every other by an edge. ${\displaystyle 2n(n-1)}$ ${\displaystyle e_{i}}$ ${\displaystyle -e_{i}}$
• It has facets that simplices of are. ${\displaystyle 2^{n}}$ ${\displaystyle \mathbb {R} ^{n-1}}$

Generally, the unit cross polytope consists of

${\displaystyle 2^{k+1}\cdot {n \choose {k+1}}}$

Components of the dimension . ${\displaystyle k}$

Symmetries

Plane of symmetry for a three-dimensional cross polytope

The unit cross-polytope is point-symmetric with respect to the coordinate origin , that is, for all true ${\displaystyle v\in \mathbb {R} ^{n}}$

${\displaystyle (v_{1},\ldots ,v_{n})\in P\Rightarrow (-v_{1},\ldots ,-v_{n})\in P}$.

Furthermore, it is symmetrical with respect to reflections on the coordinate planes , that is,

${\displaystyle (v_{1},\ldots ,v_{i},\ldots ,v_{n})\in P\Rightarrow (v_{1},\ldots ,-v_{i},\ldots ,v_{n})\in P}$

for . The coordinate planes divide the unit cross polytope into unit implices of the . ${\displaystyle i=1,\ldots ,n}$ ${\displaystyle n}$ ${\displaystyle 2^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

The resulting "cut surfaces" (cutting hyperplanes of dimension n-1) with the "coordinate planes" (coordinate hyperplanes, for n = 3 coordinate planes, for n = 2 coordinate axes) are each cross polytopes of dimension n-1.

volume

The -dimensional volume of the unit cross-polytope is ${\displaystyle n}$

${\displaystyle \operatorname {vol} (P)={\tfrac {2^{n}}{n!}}}$.

The volume is therefore arbitrarily small for the growing dimension.

Regular cross polytopes

definition

A regular cross polytope is a polytope that arises from the unit cross polytope by scaling , rotating, and translating . A polytope is therefore a regular cross polytope if there is a real number , an orthogonal matrix and a vector such that ${\displaystyle Q\subseteq \mathbb {R} ^{n}}$ ${\displaystyle \lambda >0}$ ${\displaystyle A\in \mathbb {R} ^{n\times n}}$ ${\displaystyle b\in \mathbb {R} ^{n}}$

${\displaystyle Q=\lambda AP+b}$

applies.

properties

Regular cross polytopes have the same number of vertices, edges and facets as the unit cross polytope. They also have the same symmetry properties, only the center of symmetry and the mirror planes are transformed accordingly. The volume formula is also retained and only contains an additional factor : ${\displaystyle \lambda ^{n}}$

${\displaystyle \operatorname {vol} (Q)=\lambda ^{n}\cdot {\tfrac {2^{n}}{n!}}}$.

Cross polytope (or hyperoctahedron) and dimensional polytope (or hypercube) are dual to one another . Therefore, their symmetry groups also match.

General cross polytopes

The edge graph of a four-dimensional cross polytope

definition

In general, all polytopes which are combinatorially equivalent to the unit cross polytope are called cross polytopes. To put it precisely this means:

A polytope is called a cross polytope if there is a bijection from the set of corners of onto the set of corners of a unit cross polytope such that two corners and of are connected by an edge if and only if and this is in . ${\displaystyle Q\subseteq \mathbb {R} ^{n}}$ ${\displaystyle f}$ ${\displaystyle Q}$ ${\displaystyle \{e_{1},\ldots ,e_{n},-e_{1},\ldots ,-e_{n}\}}$ ${\displaystyle P}$ ${\displaystyle v}$ ${\displaystyle w}$ ${\displaystyle Q}$ ${\displaystyle f(v)}$ ${\displaystyle f(w)}$ ${\displaystyle P}$

properties

A general cross polytope has the same number of vertices, edges, and facets as the unit cross polytope, but the symmetries are lost.

use

The cross polytope is considered to be a prototype of a polytope which (in relation to the dimension) has very few corners, but very many facets. This property is particularly important in linear optimization, since the simplex algorithm , the standard method for solving linear optimization problems, specifically checks corners for their optimality. The counterpart to this is the hypercube , the number of corners of which increases exponentially, but the number of facets only increases linearly . ${\displaystyle n}$

Web links

Commons : Polytope  - collection of images, videos and audio files

• Two representations (graphics) (PDF file, 32 kB) from the University of Stuttgart
• Brief definition by Prof. Dr. Rolfdieter Frank of the University of Koblenz-Landau on the homepage of the University of Hamburg
• Convex polytopes - WS 2003/2004 (PDF file, 416 kB) by Achill Schürmann from the Institute for Algebra and Geometry at Otto von Guericke University Magdeburg
• Polynomial representations of polyhedra (PDF file, 320 kB) by Martin Henk of the University of Magdeburg