Edge graph

Graph G.

Construction of L (G)

Edge graph L (G)

The edge graph or line graph is a term from graph theory . He defines a new graph for a given graph, which is created by swapping nodes and edges.

definition

The edge graph or line graph of a simple graph is in graph theory the graph with the following properties: ${\displaystyle L(G):=(V',E')}$ ${\displaystyle G=(V,E)}$

1. ${\displaystyle V'=E}$, that is, every edge of is a node in . ${\displaystyle G}$ ${\displaystyle L(G)}$
2. ${\displaystyle E'=\left\{\left\{e_{1},e_{2}\right\}\mid e_{1}\cap e_{2}\neq \emptyset \right\}}$, that is, two nodes from are in adjacent if the associated edges from have a common end node, i.e. are in adjacent. ${\displaystyle V'}$ ${\displaystyle L(G)}$ ${\displaystyle E}$ ${\displaystyle G}$

example

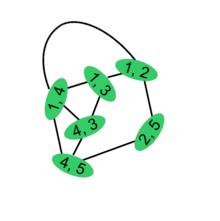
The following example illustrates the construction of the edge graph for a given graph . The graph shown has the node set and the edge set . ${\displaystyle L(G)}$ ${\displaystyle G=(V,E)}$ ${\displaystyle G}$ ${\displaystyle V=\{1,2,3,4,5\}}$ ${\displaystyle E=\{\{1,2\},\{1,3\},\{1,4\},\{2,5\},\{3,4\},\{4,5\}\}}$

A new graph is now constructed from the original , in that each edge of becomes a new node in (illustrated by the green ellipse on the original edges). The newly created nodes are connected to each other exactly when the edges collided in the original graph. ${\displaystyle G}$ ${\displaystyle e\in E}$ ${\displaystyle G}$ ${\displaystyle v'\in V'}$ ${\displaystyle L(G)}$

The result of the construction is obtained by hiding the original graph . The edge graph remains . ${\displaystyle G}$ ${\displaystyle L(G)}$

Expressed again as quantities one obtains . ${\displaystyle L(G)=(V',\{\{\{1,2\},\{1,3\}\},\{\{1,2\},\{1,4\}\},\{\{1,2\},\{2,5\}\},\dots \})}$

properties

• The edge graph of the circle graph is isomorphic to its output graph . Circle graphs (or graphs of which all components are circle graphs) are the only graphs with this property. ${\displaystyle C_{n}}$
• The edge graph of the star graph is the complete graph . ${\displaystyle S_{n}}$ ${\displaystyle K_{n}}$
• The edge graph of a bipartite graph is a perfect graph .
• Every edge graph has a Krausz partition .

literature

• Lutz Volkmann: Foundations of the graph theory . Springer, Vienna / New York 1996, ISBN 3-211-82774-9 , pp. 180 ff .

Web links

• Lutz Volkmann: Graphs on all corners and edges . Script 2006, p. 146ff (PDF; 3.51 MB)