Graph theory
The graph theory (less often also graph theory ) is a branch of discrete mathematics and theoretical computer science . The objects of consideration of graph theory are graphs ( sets of nodes and edges ), their properties and their relationships to one another.
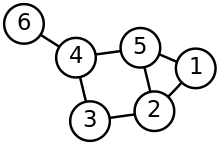
Graphs are mathematical models for network-like structures in nature and technology (such as social structures , road networks , computer networks , electrical circuits , supply networks or chemical molecules ). In graph theory one only examines the abstract network structure itself. The type, position and nature of the nodes and edges are not taken into account. However, there remain many general graph properties that can already be examined at this level of abstraction and can be found in general statements ( theorems of graph theory ). An example of this is the handshake lemma , according to which the sum of the node degrees in a graph is always even (in the adjacent figure: fourteen).
Because, on the one hand, many algorithmic problems can be traced back to graphs and, on the other hand, the solution of graph-theoretical problems is often based on algorithms , graph theory is also of great importance in computer science , especially complexity theory . The study of graphs is also part of network theory . Graphs are represented in particular by the data structures adjacency matrix , incidence matrix or adjacency list .
history
A forerunner in antiquity that was independent of graph theory was the Dihairesis method , which was used to hierarchize zoological, musicological and other terms (only partially graphically). This gave rise to early systematics within various fields of knowledge.
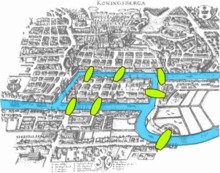
The beginnings of graph theory go back to the year 1736. At that time, Leonhard Euler published a solution to the Königsberg bridge problem . The question was whether there is a tour through the city of Königsberg (Prussia) that uses each of the seven bridges over the Pregel river exactly once. Euler was able to specify a necessary condition that could not be met for this problem and thus deny the existence of such a tour.
In 1852 the mathematician and botanist Francis Gutherie noticed that four colors are enough to color a map in such a way that two countries that border one another are always colored differently. Many mathematicians have dealt with this coloring problem . However, it was not until 1976 that the four-color theorem could be proven using a computer. It wasn't until 1997 that Neil Robertson , Daniel Sanders, Paul Seymour , Robin Thomas presented new evidence.
The term graph was first used in 1878 by the mathematician James Joseph Sylvester , based on graphic notations of chemical structures . Another founder of the early graph theory is Arthur Cayley . One of the first uses was chemical constitution formulas . (See also chemical graph theory and literature : Bonchev / Rouvray, 1990). The first textbook on graph theory appeared in 1936 by Dénes Kőnig .
In the second half of the 20th century, William Thomas Tutte worked significantly on the further development of graph theory and strongly shaped this branch of mathematics.
Subsections of graph theory
Sub-areas of graph theory are:
- Algorithmic graph theory : This sub-area deals with algorithms applicable to graphs (list of graph algorithms ) .
- Chemical graph theory : The chemical graph theory was one of the first applications of structural knowledge and applies it to chemical molecular structures.
- Extremal graph theory : The extremal graph theory studies which graphs of a given class maximize or minimize a particular graph parameter.
- Geometric graph theory and topological graph theory : These sub-areas embed graphs in planes and other geometric objects.
- Network research : In network research, complex networks are empirically examined. It finds applications in disciplines such as biology , economics and sociology .
- Probabilistic graph theory : Using a random graph , properties can be demonstrated for graphs of any size.
- Spectral graph theory (also algebraic graph theory): The spectral graph theory examines graphs on the basis of their adjacency matrices and Laplace matrices through the analysis of eigenvalues , eigenvectors and characteristic polynomials . Undirected graphs have symmetrical adjacency matrices and therefore real eigenvalues . All eigenvalues taken together are called the spectrum of the graph . While the adjacency matrix depends on the node sorting, the spectrum is independent of it.
Object viewed
In graph theory, a graph denotes a set of nodes (also called corners or points) together with a set of edges. An edge is a set of exactly two nodes. It indicates whether two nodes are related to each other or whether they are connected in the graphic representation of the graph. Two nodes that are connected by an edge are called adjacent or adjacent . If the edges are given by ordered pairs of nodes instead of sets , we speak of directed graphs . In this case a distinction is made between the edge ( a , b ) - as the edge from node a to node b - and the edge ( b , a ) - as the edge from node b to node a . Nodes and edges can also be provided with colors (formally with natural numbers ) or weights (i.e. rational or real numbers ). One then speaks of vertex or edge colored or weighted graphs.
More complex graph types are:
- Multigraphs in which the edge set of a multiset is
- Hypergraphs , in which an edge represents an arbitrarily large set of nodes (one also speaks in this case of hyper-edges )
- Petri nets with two types of knots
If the set of nodes is finite, one speaks of a finite graph , otherwise of an infinite graph .
Graph properties
Graphs can have different properties. So can a graph
- connected (generally k-connected ),
- bipartite (generally k-partit ),
- planar ,
- be Eulerian or Hamiltonian .
It can the existence of special subgraphs or minors are asked or certain parameters are examined, such as the number of nodes , number of edges , minimum degree , maximum degree , waist width , diameter , node connection speed , edge connectivity number , arc connection number , chromatic number , vertex cover number ( factor ), Independence number ( stability number ) or clique number . Two graphs can be isomorphic (structurally the same) or automorphic to one another.
The various properties can be related to one another. Investigating the relationships is a task of graph theory. For example, the node connection number is never greater than the edge connection number, which in turn is never greater than the minimum degree of the graph under consideration. In flat graphs , the number of colors is always less than five. This statement is also known as the four-color theorem .
Some of the graph properties listed can be determined algorithmically relatively quickly, for example if the effort increases at most with the square of the size of the graph. Other properties of practically applied graphs cannot be precisely determined within the lifespan of today's computers. However, in these cases the use of heuristic methods can lead to sensible approximate solutions.
Graph classes
Basically, graphs are divided into directed and undirected graphs.
Due to the context , one differentiates:
- acyclic graphs: path , path , forest , tree , DAG (directed acyclic graph)
- cyclic graphs, for example: cycle , circle , complete graph .
Due to the presence of certain properties, further graph classes can be distinguished such as
If a node is particularly distinguished, it is called a root or a rooted graph . Rooted trees are of particular importance as a tree structure .
Problems
The main problems and results of graph theory are presented below:
coloring
A well-known problem asks how many colors do you need to color the countries on a map so that no two neighboring countries are assigned the same color. The neighborhood relationship of the countries can be represented as a planar graph. The problem can now be modeled as a knot coloring problem. According to the four-color set , you need a maximum of four different colors. According to the current state of knowledge, one cannot efficiently decide whether a graph can generally be colored with fewer colors. The problem is considered to be one of the most difficult problems in the class of NP -complete problems. With the assumption that P ≠ NP , even a solution that is approximated up to a constant factor is not efficiently possible.
Search problems
An important application of algorithmic graph theory is the search for a shortest route between two locations in a road network. This problem can be modeled as a graph problem. To do this, one abstracts the road network by including all locations as nodes and adding an edge if there is a connection between these locations. The edges of this graph are weighted depending on the application , for example with the length of the associated connection. With the help of an algorithm for finding shortest paths (for example with Dijkstra's algorithm ), a shortest connection can be found efficiently. (see also: Category: Graph Search Algorithms )
Graph walkability
In terms of algorithms, it is much more difficult to determine a shortest round trip (see problem of the traveling salesman ), in which all locations on a road network have to be visited exactly once. Since the number of possible round trips increases factorially with the number of places, the naive algorithm of trying out all round trips and selecting the shortest one is only practicable for practical applications for very small networks. A number of approximation algorithms exist for this problem , which find a good but not an optimal round trip. The Christofides heuristic delivers a round trip that is a maximum of 1.5 times as long as the best possible. Assuming that P ≠ NP ( see P-NP problem ), there is no efficient algorithm for the determination of an optimal solution, since this problem is NP -hard .
The Königsberg bridge problem asks about the existence of an Euler's circle . While the Euler circle problem can be solved in linear time using the Hierholzer method , finding a Hamilton circle (a closed path in a graph that contains every node exactly once) is NP-difficult. The postman problem asks for a shortest cycle that runs through all edges at least once.
context
In the context of the connection, it is asked whether or via how many paths two nodes can be reached from one another . This plays a role, for example, when assessing the supply networks with regard to the critical (failure-threatened parts).
Clique problem
The question of the existence of (possibly maximum) cliques looks for the parts of a graph that are completely connected to one another with edges.
Node overlap
The vertex coverage problem searches for a subset of vertices in a graph that contains at least one end vertex of each edge.
Rivers and cuts in networks
With the question of the maximum flow, supply networks can be assessed in terms of their capacity.
Matching
Matching problems that can be traced back to flow problems ask about the optimal selection of edges so that no two edges are incident to a node. This can be used to solve allocation problems, for example the use of resources such as room or machine occupancy.
More graph problems
Other graph problems include
- finding a stable set ,
- the graph drawing (this exists software for visualization of graphs: yEd , Graphviz ) and
- the transformation of graphs using rule-based graph replacement systems . Graph replacement systems that are used to enumerate all graphs in a graph language are also called graph grammar
See also
literature
- Martin Aigner: Graph theory: a development from the 4-color problem. 1984 (269 pages).
- Daniel Bonchev, DH Rouvray: Chemical Graph Theory: Introduction and Fundamentals. Abacus, New York NY 1990/1991, ISBN 0-85626-454-7 .
- J. Sedlacek: Introduction to Graph Theory. BG Teubner, Leipzig 1968, 1972.
- M. Nitzsche: Graphs for Beginners (Around the House of St. Nicholas). Vieweg, Wiesbaden 2004, ISBN 3-528-03215-4 .
- R. Diestel: Graph theory. 3. Edition. Springer, Heidelberg 2005, ISBN 3-540-67656-2 ( online download ).
- Peter Gritzmann, René Brandenberg: The secret of the shortest route. A math adventure . 2nd Edition. Springer, Berlin / Heidelberg 2003, ISBN 3-540-00045-3 .
- Peter Tittmann: Graph Theory. An application-oriented introduction. 3. Edition. Hanser, Munich 2019, ISBN 978-3-446-46052-2 .
Web links
- Link catalog on graph theory at curlie.org (formerly DMOZ )
Individual evidence
- ^ Peter Tittmann: Graph theory. An application-oriented introduction . 3rd, updated edition. Munich, ISBN 978-3-446-46052-2 , pp. 1 .
- ^ Peter Tittmann: Graph theory. An application-oriented introduction . 3rd, updated edition. Munich, ISBN 978-3-446-46052-2 , pp. 76 .
- ^ Neil Robertson, Daniel Sanders, Paul Seymour, Robin Thomas: The Four-Color Theorem . In: Journal of Combinatorial Theory, Series B . tape 70 , no. 1 , 1997, ISSN 0095-8956 , pp. 2-44 .
- ↑ James Joseph Sylvester: Chemistry and Algebra. In: Nature. Volume 17, 1878, p. 284.
- ↑ Norman L. Biggs, E. Keith Lloyd, Robin J. Wilson: Graph Theory 1736-1936 . Oxford University Press, 1999, ISBN 0-19-853916-9 .
- ^ Arthur Cayley: Chemical Graphs . In: Philosophical Magazine . Volume 47, 1874, pp. 444-446.
- ↑ Dénes Kőnig: Theory of Finite and Infinite Graphs: Combinatorial Topology of Line Complexes. Academic Publishing Company, Leipzig 1936.