Petri net
As Petri networks models are discrete , mostly distributed systems referred to. The computer scientist Carl Adam Petri developed it in the 1960s on the basis of finite automata , initially not in the form commonly used today. Petri was looking for basic principles for describing concurrent switching processes, which were later condensed into axiomatic theories of concurrency .
Nowadays, variants of Petri nets are not only used in computer science for modeling , but also, for example, in theoretical biology, in the world of business processes , in mechanical engineering, logistics and many other areas. Numerous other modeling techniques such as As activity diagrams of UML 2 have adopted principles of Petri nets.
General symbolism and description
In the basic version, a network is represented as a graph , which is made up of two types of nodes , called places (or places ) or transitions . The nodes are connected by directed edges , whereby an edge connects exactly one point with a transition or vice versa. Initially, Petri considered untyped knots. A network with such nodes is called a place / transition network (short: S / T network or P / T network translated back from English as place / transition network).
Later, networks with nodes typed by markers and thus attributes to the nodes were introduced, which are evaluated as predicates at transitions and edges. A network with brands and nodes typed by them is therefore called a predicate / transition network, whereby the English-language designation Colored Petri Net (CPN) - colored Petri network - is found at least as often. The positions can be filled with any number of tokens. Such a marking represents a distributed state of the system.
The dynamics of a network result from the switching of transitions: when a transition switches, it takes labels from the places in its immediate preceding area and places labels in the places in its subsequent area, as many as are indicated on the edges. As long as the transition requires more labels than are actually there, it cannot switch yet.
Mathematical representation of a Petri net
A P / T network can be represented as a quintuple where is
- (Disjointness) and
- the (usually finite) set of places
- the (also finite) set of transitions
- the flow relation that specifies the edges. Edges always connect places with transitions or vice versa, never places with places or transitions with transitions.
- the edge weighting function, extended to by
- the start marker
The dynamics of the networks are explained in the next section.
Dynamics of Petri Nets
The following definitions and terms are helpful to describe the dynamics and other properties of Petri nets.
Before and after areas
The Vorbereich of designated with is the set of all nodes from which an edge to the node executes: .
The post set of , denoted by , is the set of nodes to which an edge from node executes: .
When switching a transition , a number of labels are taken from each position in the preceding area of the transition and a number of labels are added to each position in the subsequent area of the transition. The number of marks added or removed from each position depends on the weight of the edge between the transition and the position .
Switching rule
The switching rule in P / T networks is as follows: A transition can switch from a marking (noted ) and bring the network into the state precisely when the switching condition for is fulfilled for all positions ( is then activated or switchable ):
and the following marking is fulfilled for all positions :
- .
Switching the activated transition results in the new marking . Then you write .
Switching sequence and accessibility
A sequence of transitions with is called a switching sequence or switching sequence . If a switching sequence can be applied to a marking so that the switching condition is met for each step, then the switching sequence is called applicable to . Whether a switching sequence can be used or how a certain marking can be reached results in the accessibility problem. If there is an applicable switching sequence that converts the initial marking into , the marking can be reached . The set of all reachable markings is called the reachability set .
The switching rule results in, in the manner of operational semantics , a perhaps infinite labeled graph with a root , the reachability graph , from which all possible switching sequences and associated changes in the state of the network can be read. It should be noted, however, that this is not yet genuinely concurrent semantics, since of each concurrent set of events only the sequentializations can be viewed as switching sequences.
Due to its very simple structure, the four-seasons network from Figure 0a has a very simple reachability graph that also has four states and four transitions that exactly correspond to the transitions.
The network example from Figure 0b, on the other hand, has twice as many achievable states, since the sack of rice may or may not have fallen over regardless of the season. This net also shows the suitability of Petri nets for representing distributed states and causally independent, “concurrent” events in different parts of the system - “In China, a sack of rice falls over” and “a” can switch independently of one another because they neither have one common preconditions still have one dependent on the other.
Modeling with Petri nets
Very different variants and characteristics have been proposed for Petri nets. In the 1960s and 1970s, elementary variants were initially examined; nowadays "high-level" forms are often used. They are formally more complex, but intuitively describe the modeled system more precisely and directly.
Introductory example
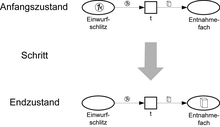
As an introductory example of a high-level network, Fig. 1 shows a model of a biscuit machine that largely abstracts the details: In the initial state, there is a coin in the machine's input slot. This enables the machine to take one step: it collects the coin and places a biscuit box in the output compartment. This is how the final state arises.
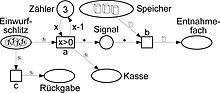
Figure 2 refines and extends the model in its initial state, in that the behavior of the inside of the machine becomes visible, together with the possible return of the inserted coin.
Components of Petri nets
The exact meaning of Figures 1 and 2 follows from the universal modeling principles of Petri nets: In a (given or planned discrete) system, one identifies a number of components that are explicitly represented in the Petri net model. This includes:
- Storage components that can contain objects or data elements (in the example: input slot, removal compartment, cash register, signal space, biscuit storage, return) and to which conditions are assigned. In the model, they are referred to as squares and graphically represented as circles or ellipses;
- Activities that can change memory contents (in Fig. 1 : t , in Fig. 2 : a , b , c ). All activities are carried out after the seats have been switched. In the model, they are called transitions and graphically represented as a square or rectangle.
- States , i.e. changing distributions of objects or data elements in storage components. ( Fig. 2 describes a state with a coin in the input slot and 3 biscuit boxes in the biscuit storage. All other storage components are empty.) In the model, a distribution of tokens to the locations forms a marking with conditions. Graphic representations (such as those in Fig. 1 and Fig. 2 ) usually show the initial marker that describes the initial state of the system.
- Objects or data elements that appear in the system, d. H. generated, transformed and consumed (in the example: coins, cookie boxes and signals). In the model they are referred to as brands and are graphically represented as “intuitively” as possible.
- Transitions from states to new states as a description of the state changes: (in the example: the transition from the initial to the final state in Fig. 1 and from the initial to an intermediate state in Figs. 2 and 3 ). In the model, such steps can be understood intuitively as a “flow of marks through the edges”.
steps
From a given marking of a Petri net model, a new marking can be reached in that a transition occurs . To do this, in must be activated . is activated when each arrow that ends with begins at a place that contains a marker that is noted on the arrow itself. In Fig. 1 , t is activated; in Fig. 2 are a and c enabled but not b . When an activated transition occurs, the markers described above disappear from their places, and for each arrow beginning with an arrow , a mark is created in the place where it ends , according to its address .
In this way, in Fig. 1 , the beginning of the marking becomes the end of the marking when t occurs. From Fig. 2 , the entry of a results in the marking shown in Fig. 3 .
The “abstract” mark (black point) on the signal square in Fig. 3 now activates transition b together with a biscuit box in the memory . As b enters, a biscuit box finally appears in the removal compartment . In Fig. 2 , transition c is also activated. If c (instead of a ) occurs, there is a mark with a coin in return .
With the above rule for the occurrence of transitions you can see immediately that coins or coins in the slot lead to a corresponding number of boxes in the removal compartment. With a second coin in the slot , transition a can occur again immediately after its first entry, regardless of the (first) entry of b .
The behavior of distributed systems
The above example shows various relationships between the activities of a distributed system. Accordingly, the occurrence of two transitions can be related in different ways. For example in Fig. 2 :
- nondeterministic
- a and c occur alternatively to each other. The coin in the slot activates the two transitions a and c . By entering one of the two, the other is no longer activated. Which of the two transitions occurs is not modeled.
- orderly
- a occurs before b : in order to enter, b needs a token that a previously created.
- concurrent
- After - as in Fig. 3 - a has entered, with a second coin in the slot ( not shown in Fig. 2 ) a can enter a second (or c a first) time, parallel to (i.e. independent of) the entry of b .
Elementary networks
Figure 4 shows a Petri-Netz model of the biscuit machine in which the brands for coins, signals and biscuit boxes are not differentiated: All are shown equally as “black” brands. Arrows do not have any inscription (according to the system of Figures 1 to 3, each arrow should be labeled with " "). Petri nets were created in this form in the 1960s and were often referred to as place / transition nets . In this case, the rules for entering a transition are particularly simple: is activated when each arrow ending at begins at a place that contains at least one marker. These marks disappear when you enter and a new mark is created at every place where an arrow that starts with ends.
Such simple marks are intuitively appropriate if (distributed) control flow is modeled, for example in the scheme of mutual exclusion in Fig. 5 : Each of the two processes and ("left" and "right") cyclically goes through the three states local , waiting , critical . The key ensures that both processes are never critical at the same time . In this example, each space always bears either no or one brand. Each place can therefore be viewed as a condition that is occasionally fulfilled and occasionally unfulfilled . Such networks are often referred to as condition / event networks .
Analysis of Petri nets
Properties of Petri Net Models
Important properties of a system should be reflected in its model. A Petri net must therefore not only represent the behavior, but also properties of a system. For example, in the nets of Figures 2 , 3 and 4, each achievable marking has the property
The number of marks on in the marking for a place denotes . For each coin in the cash register, a box of biscuits has been given or (with a token on signal) is still being given. The same applies to Fig. 5
So there is always at most one process in its critical state. An obvious, but surprisingly complicated question even for elementary system networks is the accessibility of any selected marking :
It took years to find an algorithm for this and thus prove the decidability of this accessibility problem . Other important properties of an elementary system network are:
- terminated : Each applicable switching sequence of beginning in the initial marking reaches a deadlock at some point , i.e. H. a marker that does not activate a transition. This mark is called dead (the cookie machines terminate).
- is deadlock- free : No deadlocks can be reached in (the mutual exclusion is deadlock-free).
- is alive : From every reachable marking, a marking can be reached for every transition that activates (the mutual exclusion is alive).
- is faintly alive : For every transition from there is an accessible marking that activates (biscuit machine and mutual exclusion are both faintly alive).
- is -restricted for a number : Each space contains at most tokens under each reachable marker (the biscuit machine is 3-restricted, the mutual exclusion is 1-restricted). A 1-bounded Petri net is called safe .
- is reversible : The initial marking can be reached from every accessible marking (the mutual exclusion is reversible).
- has a homestate : A homestate of is a marker that can be reached in any case from every reachable marker. Neither the biscuit machine nor the mutual exclusion has a homestate.
It should be noted that the properties of liveliness, limitation and reversibility are independent of one another.
Proof of properties
With all of the properties described , the question arises of how to prove or disprove them for a given initially marked network (see verification ). All features are available for elementary networks decidable , but only with algorithms whose complexity is much too large for practical use. In practice, therefore, algorithms are used for sufficient or necessary conditions. These algorithms are based on space invariants , initially marked traps , the marking equation and the coverage graph of a system network.
Software tools
A large number of different software tools for creating and analyzing Petri nets have been developed since the 1980s. The CPN Tools has established itself as a universal tool for high-level networks . There are also a large number of specific tools for special network variants, for example for analyzing time-sensitive and stochastic networks or for special application areas, for example service-oriented architectures.
Generalizations, special cases, variants
The most general form of high-level networks
The model of the biscuit machine in ( Fig. 1 - Fig. 3 ) is an example of a high-level network . The full expressiveness of such networks can be achieved with the help of variables and functions in the inscriptions of the arrows. As an example, Fig. 6 models a variant of the cookie machine with 4 coins in the input slot. There is no box in the store for the 4th coin; the coin should therefore be returned in any case. For this purpose, Fig. 6 contains a counter whose mark indicates the number of boxes available. The transition a is activated when the variable x takes on the current value of this mark. In addition, a with the condition x labeled> 0, which for the entry of a must be fulfilled. So every entry of a reduces the counter value by 1 and a is no longer activated at the value 0. Each additional coin ends up in the return via c .
Special case of free choice
In the model of the biscuit machine in Figures 2 , 3 and 4 , the brand in the slot non-deterministically selects one of the transitions a or c . This choice does not depend on any further preconditions; she is free .
In the system of mutual exclusion from Fig. 5 , the key has the choice between transitions b and e . This choice also depends on whether and are also selected. She is not free.
A net is a free-choice net if its structure means that all options are free, if the following applies to two arrows that start at the same place : They end at transitions where no further arrows end. Figure 7 outlines this condition. Obviously, all models of the biscuit machine are free-choice networks, but not the mutual exclusion in Fig. 5 .
Whether one of the properties described above applies or not can be decided for free-choice networks with efficient algorithms.
Generalizations of elementary networks
As early as the 1970s, elementary networks were supplemented by numerous other means of expression. Three of them are described here:
- Weight arrows : Each arrow is assigned a natural number as the "weight" . When the transition associated with the arrow occurs, marks (instead of just one mark) flow through the arrow.
- Restrict the capacity of the places : Each place is assigned a natural number as a "barrier" . If more than marks would be created when a transition occurs , is not activated. Figure 8 shows an example.
- Test a place for the absence of brands : A place is connected to a transition by a new "inhibitor" edge. is not activated if one or more bears marks. Figure 9 outlines this construction.
Weighted arrows and restricted spaces do not really increase expressiveness: they can be simulated with intuitively plausible means. In contrast, with inhibitor edges you can actually express more and consequently make fewer decisions. In particular, the accessibility for networks with inhibitor edges cannot be determined. Other means of expression are sometimes required to really model exactly how a distributed system behaves. For example, in the system of mutual exclusion in Fig. 5 , we want to show that each of the two processes may remain forever in its local state, but not forever in its critical state. We differentiate between the cold transition a (“does not necessarily occur when it is activated”) and the hot transition b (“occurs when it is activated”). It is even more complicated with transitions b and e : If we want to guarantee every waiting process that it will become critical at some point, we have to demand fairness for b and e . With the difference between hot and cold transitions and with the requirement of fairness, one can characterize the set of "intended" processes of a Petri net much more precisely.
Time-sensitive and stochastic networks
If transitions occur in an orderly manner, for example first a then b in Fig. 2 , this order should be interpreted causally and not in terms of time. Then it is logical, in Fig. 2 with a second coin in the input slot, to see the first entry of b and the second entry of a as independent of one another and not as simultaneous .
Nevertheless, there are systems with actions, the duration of which is to be modeled, or which are in some way oriented towards clocks. Numerous variants of time-affected Petri nets have been proposed for modeling such systems. Places, transitions, marks and arrows are provided with time stamps and time intervals. These additions regulate the activation of transitions and generate new time stamps after a transition has occurred.
If two transitions and compete for the same mark of a mark (for example, in Fig. 5 b and e compete for the mark on the key) and if it is reached again and again, one occasionally wants to model that it occurs with probability and with probability . The broad theory of stochastic networks is suitable for this .
Higher Petri Nets
In order to uniformly describe systems that contain mobile components as subsystems, Petri network formalisms were developed in which the brands are in turn interpreted as network instances. With these so-called networks in networks , a number of semantic variants are possible, which differ, among other things, with regard to the question of whether trademarks are to be understood as network copies or merely as references.
These formalisms arise from an object-oriented approach in which copies of classes (network patterns) can be generated and communication between objects is possible via defined interfaces.
Some of the early representatives are the object Petri nets from Lakos (today, in view of intensive further development, mainly of historical importance) and Valk, who originally introduced them together with Jessen in the context of order systems.
The historical development
The beginning
Research on Petri nets began with the thesis of Carl Adam Petri in 1962. This work was initially largely ignored; the Theoretical computer science at that time pursuing other issues and for the practice came Petris suggestions too early. A first breakthrough in the theory came in the late 1960s with the use of Petris ideas in the Project MAC of MIT . In the 1970s, place / transition networks were studied around the world, but quite often from the narrow perspective of formal languages.
The development since the 1980s
Since the early 1980s, very different variants of high-level networks have been proposed that use objects, data elements or symbols as trademarks. These formalisms increase the expressiveness of place / transition networks considerably. At the same time, many analysis techniques of place / transition networks could be generalized to these formalisms.
With increasing interest in distributed systems and distributed algorithms, numerous new modeling techniques have been and are being proposed since the 1980s. Petri nets held their own against these new developments; they are often used as a measure of quality and expressiveness for models of distributed systems. Provides an overview of numerous areas of application of Petri nets.
Current topics
Nowadays, Petri nets are used to model systems whose behavior consists of discrete, locally limited steps. These are often systems that integrate computers or that are simulated with computers. The modeling of processes in systems biology, the world of business processes and service-oriented architectures are currently particularly promising applications of Petri nets.
For further reading
In the fifty years since the beginnings of the Petri nets, a multitude of variants and areas of application has emerged, the large extent of which excludes a complete, systematic representation. Anyone who would like to get to know the diverse aspects of Petri nets will find a suitable start in the Petri Netz portal of the University of Hamburg PetriWorld . The Advanced Course on Petrinets summer school series (most recently the 5th course in Rostock, 2010) and the annual Conference on Applications and Theory of Petri Nets give current overviews and presentations. Among the numerous textbooks is current.
application areas
- Asynchronous circuit
- Concurrent programming
- Parallel algorithm
- Software design
- Management of work processes
- Verification of concurrent processes
- Automation (control technology)
- Material flow network
- Business process modeling
See also
Norms and standards
- ISO / IEC 15909-1: Software and systems engineering - Higher Petri nets - Part 1: Terms, definitions and graphical notation (currently only available in English)
- ISO / IEC 15909-2: Software and systems engineering - Higher Petri nets - Part 2: Transfer format (currently only available in English)
Web links
- Section “Petri Networks and Related System Models” of the Society for Computer Science
- Overview of software tools for the creation of Petri nets (English)
- Petri Nets World (English)
- Informal introduction (PDF file; 768 kB)
References
- ↑ a b Dirk Abel : Petri networks for engineers. Modeling and analysis of discretely controlled systems. Springer, Berlin uu 1990, ISBN 3-540-51814-2 .
- ↑ Bernd Baumgarten: Petri networks. Basics and Applications. 2nd Edition. Spectrum - Akademischer Verlag, Heidelberg et al. 1996, ISBN 3-8274-0175-5 .
- ↑ a b c d Wolfgang Reisig: Petri networks. Modeling technology, analysis methods, case studies. Vieweg + Teubner, Wiesbaden 2010, ISBN 978-3-8348-1290-2 .
- ↑ Ernst W. Mayr : An algorithm for the general Petri net reachability problem. In: SIAM Journal on Computing. Vol. 13, No. 3, 1984, pp. 441-460, doi : 10.1137 / 0213029 .
- ^ Tadao Murata: Petri nets: Properties, Analysis and Applications. In: Proceedings of the IEEE . Vol. 77, No. 4, April 1989, pp. 541-580, doi : 10.1109 / 5.24143 .
- ^ Kurt Jensen, Lars M. Kristensen: Colored Petri Nets. Modeling and Validation of Concurrent Systems. Springer, Berlin uu 2009, ISBN 978-3-642-00283-0 .
- ^ The Petri Net World
- ↑ a b www.service-technology.org .
- ↑ a b Jörg Desel, Javier Esparza: Free Choice Petri Nets (= Cambridge Tracts in Theoretical Computer Science. Vol. 40, 1995). Cambridge University Press, Cambridge et al. 1995, ISBN 0-521-46519-2 .
- ↑ Christophe Reutenauer: The mathematics of Petri nets. Prentice-Hall International, Hemel Hempstead 1990, ISBN 0-13-561887-8 .
- ↑ Marco Ajmone Marsan, Gianfranco Balbo, Gianni Conte, Susanna Donatelli, Giuliana Franceschinis: Modeling with Generalized Stochastic Petri Nets. Wiley, Chichester et al. 1995, ISBN 0-471-93059-8 .
- ^ Charles Lakos: From colored Petri nets to object Petri nets. In: Giorgio De Michelis, Michel Diaz (eds.): Application Theory of Petri Nets 1995. 16th International Conference Turin, Italy, June 26-30, 1995. Proceedings (= Lecture Notes in Computer Science . 935). Springer, Berlin et al. 1995, ISBN 3-540-60029-9 , pp. 278-297.
- ↑ Eike Jessen , Rüdiger Valk: computing systems. Basics of modeling (= study series computer science. ). Springer, Berlin et al. 1987, ISBN 3-540-16383-2 .
- ^ Carl Adam Petri: Communication with automata (= writings of the Rheinisch-Westfälisches Institut for instrumental mathematics at the University of Bonn. 2, ZDB -ID 405247-x ). Mathematical Institute of the University of Bonn, Bonn 1962, (at the same time: Darmstadt, Technical University, dissertation, 1962).
- ↑ James L. Peterson: Petri Net Theory and the Modeling of Systems. Prentice-Hall, Englewood Cliffs NJ 1981, ISBN 0-13-661983-5 .
- ^ Claude Girault, Rüdiger Valk: Petri Nets for Systems Engineering. A Guide to Modeling, Verification, and Applications. Springer, Berlin et al. 2003, ISBN 3-540-41217-4 .
- ^ Ina Koch, Wolfgang Reisig, Falk Schreiber (eds.): Modeling in Systems Biology. The Petri Net Approach (= Computational Biology. 16). Springer, London uu 2011, ISBN 978-1-84996-473-9 .
- ↑ Wil van der Aalst , Christian Stahl: Modeling Business Processes. A Petri Net-Oriented Approach. The MIT Press, Cambridge MA et al. 2011, ISBN 978-0-262-01538-7 .