Finite automaton
A finite state machine ( EA , also state machine , state machine ; English finite state machine , FSM ) is a model of a behavior, consisting of states , state transitions and actions . An automaton is called finite if the set of states that it can assume (later called S) is finite. A finite automaton is a special case from the set of automata .
A state can contain information about the past, since the system has reached it on its previous way. I.e. to a certain extent it reflects the changes in the input from the system start up to the current point in time.
A state transition is a transition from the current state to a new (different) state. This transition occurs when the specified logical conditions / "inputs" are present that must be met in order to enable the transition.
An action is the "issuance" of the EA, which occurs in a certain situation. There are four types of actions:
- Input Action: The action is executed / issued when entering (was matter over which state transition the state achieved if there are several) in a state.
- Output Action: The action is at the exit generated a state (no matter left over which state transition of the state).
- Input action: The action is generated depending on the current status and the input. Several actions can be assigned to a state, which are carried out depending on the state transition via which it is reached / exited.
- Transition action: The action is executed dependently / during a state transition.
An EA can be represented as a state transition diagram as in Figure 1. In addition, several types of transition tables (or state transition tables) are used. The following table shows a very common form of transition tables: The combination of the current state (B) and input (Y) leads to the next state (C). Complete information about the possible actions is given with the help of footnotes. A definition of the EA that also includes the full output information is possible with status tables that are individually defined for each status (see also virtual EA ).
| Current state / element of the input alphabet |
Element of the input alphabet 1 | Element of the input alphabet 2 | Element of the input alphabet 3 |
|---|---|---|---|
| Condition a | ... | ... | ... |
| Condition B | ... | State C. | ... |
| State C. | ... | ... | ... |
The definition of EA was originally introduced in automaton theory and later adopted in computer technology.
State machines are mainly used in the development of digital circuits, modeling of application behavior (controls), in general in software technology as well as word and speech recognition.
Classification
In general, there are two groups of EA: acceptors and transducers.
Acceptors
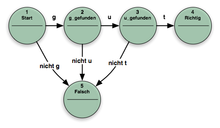
They accept and recognize the input and signal the result to the outside world through their state. Usually symbols (letters) are used as input. The example in Figure 2 shows an EA that accepts the word “good”. Acceptors are mainly used in word and speech recognition.
Transducers
Transductors generate outputs depending on the state and input with the help of actions. They are mainly used for control tasks, a basic distinction being made between two types:
- Moore machine
- In the Moore model , only entry actions are used; i.e. the output (Γ) only depends on the state (S) (S → Γ). Compared to the Mealy model, the behavior of a Moore machine is simpler and easier to understand. The example in Figure 3 shows a Moore machine that controls an elevator door. The state machine knows two commands, "open" and "close", which can be entered by a user. The entry action (E :) in the "Open" state starts a motor that opens the door, and the entry action in the "Close" state starts the motor in the opposite direction. The input actions in the "Open" and "Close" states stop the motor. They also signal the situation to the outside world (e.g. to other EA).
- Mealy machine
- In the Mealy model , input actions are used; i.e., the output (Γ) depends on the state (S) and the input (Σ) (S × Σ → Γ). The use of Mealy machines often leads to a reduction in the number of states to be considered. This makes the function of the EA more complex and often more difficult to understand. The example in Figure 4 shows a Mealy EA that behaves in the same way as the EA in the Moore example. There are two input actions (I :): “start the motor to close the door when the input is 'close'” and “start the motor in the opposite direction to open the door when the input is 'open' ".
If the time behavior can be disregarded, Moore and Mealy machines are equivalent. Under this condition, one can be converted into the other; mixed models are often used in practice. In the area of synchronous system design ( digital electronics ), on the other hand, there are important differences that must not be ignored. These concern both the different number of states and the time characteristics of the control signals generated.
A further classification of the EA is made by the distinction between deterministic (DEA) and non-deterministic (NEA) automata. In the deterministic automata there is exactly one transition for every possible input for every state. With the non-deterministic automata there can be no or more than one transition for the possible input.
An EA that consists of only one state is called a combinatorial EA. He only uses input actions.
The logic of the EA
The next state and the output of the EA is a function of the input and the current state. Figure 5 shows the logic flow.
The mathematical model
There are different definitions depending on the type of DEA . An acceptor is a 5-tuple (Q, s, Σ, F, δ), where:
- Q is the finite set of states (q 0 - q x )
- s is the starting state (s is an element of Q)
- Σ is the finite input alphabet
- F is the final state set (F is a subset of Q)
- δ is the transition function , it can be represented as an automaton table or as a state transition graph.
A transducer is a 7-tuple (Σ, Γ, S, s 0 , F, δ, ω), where:
- Σ is the input alphabet (a finite non-empty set of symbols),
- Γ is the output alphabet (a finite non-empty set of symbols),
- S is a finite non-empty set of states,
- F is the final state set (F is a subset of S)
- s 0 is the initial state and an element of S,
- δ is the state transition function: δ: S x Σ → S,
- ω is the output function: ω: S x Σ → Γ,
If the output function is a function of the state and input alphabet (ω: S x Σ → Γ), then it is a Mealy model. If the output function only depends on the state (ω: S → Γ), then it is a Moore model.
optimization
An EA is optimized by finding the state machine with the smallest number of states that fulfills the same function. This problem can be solved with the help of coloring algorithms, for example .
Homing sequences and UIO sequences
Homing episodes
A homing sequence (also known as homing sequence) is a sequence of inputs, so that the outputs can be used to determine the status of the machine afterwards. In this way, in the case of strongly connected state machines, a sequence can be found very easily in order to return to the initial state, i.e. home . Every minimal state machine has a homing sequence.
| input | possible state quantities (at which output) |
|---|---|
| ε | |
| a | |
| aa | |
| from | |
| b |
UIO episodes
A UIO sequence (Unique-Input-Output-Sequence) is a sequence of inputs to use the outputs to determine the state from which you started. Such a sequence does not always exist, the problem of finding one is PSPACE -complete.
Example UIO sequences for Fig. 6:
- : a / 0, a / 0, b / 1
- : a / 1
- : b / 0
implementation
hardware
In digital circuits, EA are built with the help of programmable logic controllers, logic gates, flip-flops or relays. A hardware implementation normally requires a register to store the state variable, a logic unit that determines the state transitions, a second logic unit that is responsible for the output, and a clock or a delay element to switch / differentiate between the previous, current and subsequent state to be able to.
software
In software development, the following concepts are mostly used to model or implement applications with the help of state machines:
Real computers as EA servers
All digital computers that exist in the real world have a finite memory size and can therefore only accept a finite (albeit very high) number of digital switching states. They can therefore be viewed as a subset of the finite automata. However, for theoretical considerations it is often more useful to consider them as a subset of more powerful machine models such as the Turing machine .
Representation of finite automata
The general rules for drawing a state transition diagram are as follows:
- Circles represent states. The name of the state is in the circle.
- Arrows between states represent the transitions. Each arrow shows which conditions enable the transition.
See also
literature
- John E. Hopcroft , Jeffrey Ullman : Introduction to Automata Theory, Formal Languages, and Complexity Theory . 2nd Edition. Addison-Wesley , Bonn, Munich 1990, ISBN 3-89319-181-X (Original title: Introduction to automata theory, languages and computation .).
- Peter Sander, Wolffried Stucky, Rudolf Herschel: Automata, Languages, Predictability. Teubner, Stuttgart 1992, ISBN 3-519-02937-5 .
- Ferdinand Wagner: Modeling Software with Finite State Machines: A Practical Approach. Auerbach, Boca Raton 2006, ISBN 0-8493-8086-3 .
- Zvi Kohavi: Switching and Finite Automata Theory. McGraw-Hill, New York 1978, ISBN 0-07-035310-7 . (English)
- Arthur Gill: Introduction to the Theory of Finite-state Machines. McGraw-Hill, New York 1962. (English)
- Heinz-Dietrich Wuttke, Karsten Henke: Switching systems - a machine-oriented introduction. Pearson Studium, Munich 2003, ISBN 3-8273-7035-3 .
Web links
- Formal Languages and Abstract Automata - Course by Tino Hempel
- Kara - programming with finite automatons - course: playfully program the ladybug "Kara" as an EA and solve tasks.
- JFLAP - Java program for creating all kinds of machines
- FSMCreator - Java program for creating finite automata (English)
- Sinelabore - Generates C / C ++ / Java code from UML state diagrams. The focus is on embedded systems. (English)
- Automaton - Java source code example for a finite automaton (English, German comments)
- YAKINDU Statechart Tools - An open source tool for the specification and development of reactive, event-driven systems with the help of state machines
- C ++ Fsm Framework , an event-driven state machine framework for C ++ with PERL script to generate PLANTUML files for FSM documentation.
- Testing - by Alexander Knapp with an algorithm for homing sequences
Individual evidence
- ^ Pong P. Chu: RTL Hardware Design using VHDL. Wiley Interscience, 2006, ISBN 0-471-72092-5 , Chapter 10, especially 10.4: Moore machine versus Mealy machine.