PSPACE

In complexity theory , PSPACE denotes the class of decision problems that can be decided by deterministic Turing machines with polynomial space .

Alternative characterizations

According to Savitch's theorem , PSPACE is equal to the class NPSPACE , the class of problems decidable in polynomial space by a nondeterministic Turing machine .

For the complexity class IP , which contains all decision problems that an interactive proof system possesses, the following applies: IP = PSPACE.

AP = PSPACE also applies to the class AP of the languages recognized by alternating Turing machines in polynomial time.

If one-way functions exist, then CZK = IP = PSPACE also applies to the class CZK of the languages for which (computational) zero-knowledge proofs exist.

Problems in PSPACE

There are many problems in PSPACE to which all other PSPACE problems in polynomial time can be reduced . These so-called PSPACE- complete problems are assumed not to be in NP.

The canonical PSPACE-complete problem is the satisfiability problem for quantified Boolean formulas .

Another PSPACE-complete problem is deciding whether a given word can be generated from a given context-sensitive grammar .

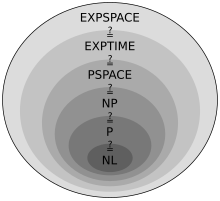
Relationship to other complexity classes

Relation to other complexity classes

The relationship to other known complexity classes is as follows:

NC P NP PSPACE

{\ displaystyle \ subseteq}

{\ displaystyle \ subseteq}

{\ displaystyle \ subseteq}

NC PSPACE

{\ displaystyle \ subset}

All of the above inclusions are believed to be real:

NC P NP PSPACE

{\ displaystyle \ subset}

{\ displaystyle \ subset}

{\ displaystyle \ subset}

The inclusion of NP PSPACE results from the fact that it only has to be shown for any NP-difficult problem that it is in PSPACE. This is the case for SAT , for example : there is an exponential number of assignments for the variables, but each of these assignments can be stored in polynomial space. In this way, all assignments can be enumerated and tried out one after the other, whereby SAT can be answered, and thus all other problems in NP. ${\ displaystyle \ subseteq}$

Individual evidence

^ Adi Shamir: IP = PSPACE . In: Proceedings of IEEE FOCS'90 . IEEE, 1990, pp. 11-15 , doi : 10.1109 / FSCS.1990.89519 .
^ Sanjeev Arora and Boaz Barak: Computational Complexity: A Modern Approach . Cambridge University Press, 2009, ISBN 978-0-521-42426-4 , pp. 100 ( princeton.edu ).
↑ Michael Ben-Or , Oded Goldreich , Shafi Goldwasser , Johan Håstad , Joe Kilian , Silvio Micali , Phillip Rogaway : Everything Provable is Provable in Zero-Knowledge . In: CRYPTO '88 (= LNCS ). tape 403 . Springer, 1990, p. 37-56 , doi : 10.1007 / 0-387-34799-2_4 .

Web links

PSPACE . In: Complexity Zoo. (English)

[Sha90-1] Adi Shamir: IP = PSPACE . In: Proceedings of IEEE FOCS'90 . IEEE, 1990, pp. 11-15 , doi : 10.1109 / FSCS.1990.89519 .

[AB100-2] Sanjeev Arora and Boaz Barak: Computational Complexity: A Modern Approach . Cambridge University Press, 2009, ISBN 978-0-521-42426-4 , pp. 100 ( princeton.edu ).

[BBG88-3] Michael Ben-Or , Oded Goldreich , Shafi Goldwasser , Johan Håstad , Joe Kilian , Silvio Micali , Phillip Rogaway : Everything Provable is Provable in Zero-Knowledge . In: CRYPTO '88 (= LNCS ). tape 403 . Springer, 1990, p. 37-56 , doi : 10.1007 / 0-387-34799-2_4 .