Complexity theory
The complexity theory as a branch of theoretical computer science deals with the complexity algorithmically intractable problems at different formal computer models . The complexity of algorithms is measured in terms of their resource consumption , usually computing time or storage space requirements , sometimes also more specific measures such as the size of a circuit or the number of processors required for parallel algorithms . The complexity of a problem is in turn the complexity of the algorithm that solves the problem with the least possible consumption of resources.
The complexity theory differs from the computability theory , which deals with the question of which problems can in principle be solved algorithmically. In contrast, the most important research goal of complexity theory is to classify the set of all solvable problems. In particular, an attempt is made to delimit the set of efficiently solvable problems, the consumption of resources of which can be managed in practice, from the set of inherently difficult problems.
Classification in theoretical computer science
Complexity theory is one of the three main areas of theoretical computer science , alongside computability theory and the theory of formal languages . One of her main research goals is the classification of problems with regard to the effort required to solve them. The delimitation of the practically efficiently solvable problems plays a special role. Complexity theory therefore limits those problems for which other disciplines of computer science should sensibly search for efficient solutions, and thus motivates the development of practical approximation algorithms .
In addition to the pure gain in knowledge, the method arsenal of complexity-theoretical research also enriches numerous related areas. For example, their close interlinking with automaton theory leads to new machine models and a more comprehensive understanding of how automatons work. The often constructive evidence is also used in the context of the design and analysis of algorithms and data structures .
Problems from the perspective of complexity theory
Decision Problems as Formal Languages
The central subject of complexity theory are problems , usually decision problems , the instances of which require a yes / no answer. A decision problem is often presented as formal language . Each instance of the problem is expressed as a word over an alphabet; H. as a sequence of characters from this alphabet. The language in question consists of the words to which an instance with the answer “yes” corresponds. The task then consists in solving the word problem , i.e. in deciding for a given word whether it belongs to the language or not, and with that one has also found the answer to the corresponding problem instance.
For example, if the problem is to decide whether a graph contiguous or not, then a word would be a representation of any graph . The associated language to be decided would be the set of words that represent a coherent graph.
One might assume that the restriction to decision problems excludes many important problems. However, there is also a corresponding decision problem for all problems relevant in the sense of complexity theory. If one considers, for example, the problem of the multiplication of two numbers, the corresponding language of the decision problem consists of all triples of numbers for which the relationship applies. Deciding whether a given triple belongs to this language is equivalent to solving the problem of multiplying two numbers.
Calculation problems as illustrations
In addition to decision problems, one also considers calculation problems. This requires an answer that describes the solution to the problem. The multiplication problem, for example, usually presents itself in practice as a calculation problem: You want to find the product of two numbers.
One understands a computation problem as a mapping from a domain of definition into a solution space, in the case of the multiplication of natural numbers as a mapping . Another example is the traveling salesman problem . Here one looks for the optimal order in which to visit given places, whereby the total length of the route should be minimal. Many optimization problems are of great practical importance. For the definition of most complexity classes, however, the formulation by decision problems is preferred.
Optimization problems represent an important sub-category of calculation problems . In the case of optimization problems, the functional relationship consists of the requirement to determine the maximum or minimum of a given cost function over all possible solutions to the problem. In the case of the traveling salesman problem, the length of the optimal route would have to be calculated.
Problem instances
A problem instance is not to be confused with the problem itself. In complexity theory, a problem represents a general question, a template. An instance of the problem is then a complete question which defines the correct answer (yes or no in the case of a decision problem).
One instance of the traveling salesman problem could be, for example, the question of whether a route through the state capitals of Germany with a maximum length of 2000 km exists. Deciding which route to take has limited value for other instances of the problem, such as a tour of the sights of Milan . In complexity theory one is therefore interested in statements that are independent of concrete instances.
A problem is formulated in such a general way that it defines an infinite set of problem instances, because it does not make sense to ask about the complexity of a finite set of instances; a program could contain a list of ready-made answers and only return the correct solution by accessing a table, which does not reflect the effort required to determine the answers. It only becomes interesting when there is an infinite number of instances and you want to find an algorithm that calculates the correct answer for each instance.
Problem representations
As formal languages, problems and their instances are defined using abstract alphabets . The binary alphabet with the symbols 0 and 1 is often chosen, as this comes closest to the use of bits in modern computers. Entries are then coded using alphabet symbols. Instead of mathematical objects such as graphs, a bit sequence may be used that corresponds to the adjacency matrix of the graph, instead of natural numbers, for example, their binary representation .
Even if proofs of complexity-theoretical statements usually make use of concrete representations of the input, one tries to keep statements and considerations independent of representations. This can be achieved, for example, by ensuring that the selected representation can, if necessary, be transformed into another representation without too much effort, without the overall computation effort being significantly changed as a result. In order to make this possible, among other things, the selection of a suitable universal machine model is important.
Problem size
Once a problem has been formally defined (for example the traveling salesman's problem in the form of a graph with edge weights), one would like to make statements about how an algorithm behaves when calculating the problem solution depending on the difficulty of the problem. In general, there are many different aspects to consider in assessing the severity of the problem. Nevertheless, it is often possible to find a few scalar quantities that significantly influence the behavior of the algorithm with regard to resource consumption. These sizes are known as the problem size. As a rule, this corresponds to the input length (in the case of a specifically selected representation of the input).
One now examines the behavior of the algorithm as a function of the problem size. The complexity theory is interested in the question: How much extra work is necessary for increasing problem sizes? Does the effort (in relation to the size of the problem) increase linearly , polynomially , exponentially or even over- exponentially ?
In the case of the traveling salesman problem, for example, the problem size can be defined as the number of given locations (neglecting that the given route lengths can also have input variables of different sizes). Then this problem is trivial for problem size 2, since there is only one possible solution here and it must therefore also be optimal. However, as the problem size increases, an algorithm will have to do more work.
Best, worst and average case for problem sizes
Different behaviors of algorithms can also be observed within a problem size. The problem of the traveling salesman for the 16 German state capitals has the same problem size as finding a route through 16 European capitals. It is by no means to be expected that an algorithm will work equally well under the different conditions (even with the same problem size). However, since there are usually an infinite number of instances of the same size for a problem, they are usually roughly grouped into three groups: best, average and worst case. These stand for the questions:
- Best case: How does the algorithm (in relation to the resource in question) work in the best case?
- Average case: How does the algorithm work on average (although the underlying distribution for calculating an average is not always obvious)?
- Amortized case: how does the algorithm work in the worst case for a sequence of runs?
- Worst case: how does the algorithm work in the worst case?
The functions in the results of the questions are ordered in ascending order, if they are clearly indicated, i.e. This means: a problem that has amortized, for example, quadratic demand has (at most) quadratic demand also on average and in the worst case no less.
Lower and upper bounds for problems
The consideration of the best, worst and average cases always relates to a fixed input length. Even if the consideration of specific input lengths can be of great interest in practice, this perspective is usually not abstract enough for complexity theory. Which input length is considered large or practically relevant can change very quickly due to technical developments. It is therefore justified to investigate the behavior of algorithms in relation to a problem completely independently of concrete input lengths. For this purpose, one considers the behavior of the algorithms for ever increasing, potentially infinitely large input lengths. One speaks of the asymptotic behavior of the respective algorithm.
In this investigation of the asymptotic resource consumption, lower and upper bounds play a central role. So you want to know which resources are at least and at most needed to resolve a problem. The lower bounds are of particular interest for complexity theory: One would like to show that a certain problem requires at least a certain consumption of resources and that there can therefore be no algorithm that decides the problem with fewer resources. Such results help to separate problems in terms of their difficulty over the long term. However, so far only comparatively few meaningful lower bounds are known. The reason for this lies in the problem that investigations of lower bounds must always refer to all conceivable algorithms for a problem; thus also on algorithms that are not even known today.
In contrast, the proof of upper bounds is usually achieved by analyzing specific algorithms. By proving the existence of even one algorithm that complies with the upper bound, the proof is already provided.
In the case of certain problems, such as the complexity of encryption methods, an attempt is made to prove that the expected consumption of resources when attempting to break the method exceeds any realistic level. The term transcomputational problem was coined for problems that cannot be solved even with a computer the size of the earth during the life of the earth .
Machine models in complexity theory
Cost functions
In order to analyze the resource consumption of algorithms, suitable cost functions must be defined, which enable the work steps of the algorithm to be assigned to the resources used. In order to be able to do this, it must first be determined which type of work step is allowed for an algorithm. In complexity theory, this definition is made using abstract machine models - if real computer models were used, the knowledge gained would be out of date in just a few years. The work step of an algorithm takes place in the form of a command execution on a certain machine. The commands that a machine can execute are strictly limited by the respective model. In addition, different models differ in how they handle the memory and in their capabilities for parallel processing, i.e. H. the simultaneous execution of several commands. The cost function is now defined by assigning cost values to the commands that are allowed in each case.
Cost measures
Often, different costs for different commands are abstracted and 1 is always set as the cost value for command execution. For example, if addition and multiplication are the permitted operations on a machine , then the cost value of 1 is added for each addition and each multiplication that must be calculated in the course of the algorithm. One then speaks of a uniform cost measure . Such a procedure is justified if the permitted operations do not differ significantly and if the range of values on which the operations work is only limited. This is already clear for a simple operation like multiplication: the product of two single-digit decimal numbers should be calculated much faster than the product of two hundred-digit decimal numbers. With a uniform cost measure, both operations would still have a cost of 1. If the possible operands actually differ so significantly in the course of an algorithm, a more realistic cost measure must be selected. Often one then chooses the logarithmic cost measure . The reference to the logarithm results from the fact that a decimal number n can essentially be represented by binary digits. You select binary digits to represent the operands and define the permitted Boolean operations . If the respective machine model uses addresses, these are also coded in binary. In this way the costs are weighted logarithmically over the length of the binary representation. Other cost measures are possible, but are rarely used.
Machine models and problems
A distinction is made between different calculation paradigms: the most pragmatic type is certainly that of the deterministic machines; there is also the type of nondeterministic machine that is particularly relevant in theory ; there are still probabilistic machines , alternating and others. In general, any machine model can be defined using any of the paradigms above. Some paradigms, such as nondeterminism, model a type that has to be reserved for theory, since nondeterminism cannot be physically built in the form defined there (you can "guess" a correct path in a calculation tree ) however, often easy to construct to a given problem. Since a transformation from nondeterministic to deterministic machines is always relatively easy, one therefore first constructs a nondeterministic machine version and later transforms it into a deterministic one.
From this emerges an important proof technique of complexity theory: If a certain type of machine can be constructed for a given problem, on which the problem can be resolved with certain costs, then the complexity of the problem can already be estimated. In fact, even the different machine models are used as a basis for the definition of complexity classes . This corresponds to an abstraction from a concrete algorithm: If a problem can be decided on the machine (although a corresponding algorithm may not yet be known), it can be assigned directly to a certain complexity class, namely that which is defined by. This relationship between problems and machine models enables evidence to be drawn up without the cumbersome analysis of algorithms.
Frequently used machine models
The most common models are:
To investigate problems that can be parallelized, parallelized versions of these machines can also be used, in particular the parallel register machine .
The extended Church-Turing thesis
For the use of machine models in complexity theory, an extension of the Church-Turing thesis is important, which is also known as the extended Church-Turing thesis . It says that all universal machine models are equally powerful in terms of computing time, except for polynomial factors. This allows the complexity theorist a relatively free choice of the machine model with regard to the respective research objective. This thesis too cannot be proven; In contrast to the usual Church-Turing thesis, it would be possible to refute it with a counterexample.
Model modifications for storage space analysis
In order to examine the minimum memory requirements that are required to solve problems, the following modifications are often made to the machine model used (usually a Turing machine):
- The input memory may only be read .
- The output may only be written to. The write head is only moved after writing and always in the same direction (if the machine model allows such a movement).
Input and output of the machine can then be disregarded for the investigation of the memory requirement. The motivation for these changes is as follows: If, for example, the input memory were included in the memory space analysis, no problem could be solved in less than space requirements, because the input word always has exactly the length and thus the memory requirement n legible, it prevents it from being used for interim invoices. You can then neglect the input when calculating the space requirement. Similar reasoning leads to the limitation of the output. The additional restriction of possible head movement prevents the head position from being used to “memorize” information. Overall, all these restrictions ensure that input and output do not have to be taken into account in the storage space analysis.
The modifications made only influence the time behavior of the machine by a constant factor and are therefore negligible.
Use and justification of the O notation
When investigating the order of magnitude for effort, complexity theory makes extensive use of the O notation . Linear factors and constants are hidden from view. This approach may come as a surprise at first, as it would often be very important for the practitioner to halve the effort.
The point of view of complexity theory can theoretically be justified with a technique called linear acceleration or the speed-up theorem . (We limit ourselves here to the time behavior. Analogue proofs can also be given for the memory requirement or other resources.) The Speedup theorem simply states that for every Turing machine that decides a problem in time , a new Turing machine can be constructed that the problem is less than resolved in time . Any small size can be chosen. That means nothing else than that every Turing machine that solves a certain problem can be accelerated by any constant factor. The price for this acceleration consists in a greatly increased working alphabet size and state set of the Turing machine used (ultimately "hardware").
This acceleration is achieved regardless of the size of the problem. Therefore, when considering the asymptotic behavior of problems, it does not make sense to consider constant factors - such factors can be eliminated by using the acceleration technique. The neglect of constant factors, which is expressed in the O notation, therefore not only has practical reasons, it also avoids falsifications in the context of complexity-theoretical considerations.
Creation of complexity classes
An essential task of complexity theory is to define meaningful complexity classes , to sort the problems at hand into these and to find statements about the mutual relationships between the classes.
Influencing variables in the formation of complexity classes
A number of factors influence the formation of complexity classes. The main ones are the following:
- The underlying calculation model (Turing machine, register machine, etc.).
- The calculation mode used (deterministic, nondeterministic, probabilistic, etc.).
- The computational resource under consideration (time, space, processors, etc.).
- The assumed measure of cost (uniform, logarithmic).
- The barrier function used .
Requirements for barrier functions
To specify or define complexity classes using barrier functions . For example, if you write DTIME (f), you mean the class of all problems that can be decided on a deterministic Turing machine in time . is a barrier function. In order to be able to be used as a barrier function for complexity-theoretical analyzes, the function should at least meet the following requirements:
- (Step number, memory etc. are calculated as natural numbers).
- (monotonous growth).
- The function itself must be calculable in terms of time and space . (Space / time constructability)
A function that meets these requirements is also referred to as a real complexity function . The purpose of the requirements is partly of a technical nature. The barrier function itself can flow into evidence in a constructive way (for example as a Turing machine) and should therefore behave “benign” for these purposes. At this point it should only be pointed out that a certain degree of caution must be exercised when choosing the barrier function, because otherwise certain algorithmic techniques cannot be used.
Most of the functions that occur in practice correspond to the above restrictions, such as the constant function, the logarithmic function , the square root function , polynomials , the exponential function and all combinations of these functions. The following is an overview of the most important barrier functions with the usual way of speaking. As usual, it is specified in O notation .
The most important barrier functions
| constant | |
| logarithmic | |
| polylogarithmic | For |
| linear | |
| linearithmic | |
| square | |
| polynomial | For |
| exponentially | For |
Hierarchy records
For the educated classes, one would like to prove as far as possible that more problems can actually be solved with additional resources . These proofs are called hierarchy sets (also called separation sets), as they induce a hierarchy on the classes of the respective resource. So there are classes that can be put into a real subset relationship. Once such real subset relationships have been determined, statements can also be made about how large the increase in a resource must be in order to be able to calculate a larger number of problems. The resources of time and space are of particular interest. The induced hierarchies are also referred to as the time hierarchy and the spatial hierarchy .
The hierarchy sets ultimately form the foundation for the separation of complexity classes. They form some of the earliest findings in complexity theory. It must be added that all hierarchy records are based on various requirements. One of these prerequisites is, for example, that the above-mentioned requirements for real complexity functions are met. If these requirements are not met, the entire class hierarchy will actually collapse.
Time hierarchy set
The time hierarchy theorem states:
So there are problems whose asymptotic time requirement on a deterministic Turing machine within the class is not in . A similar relationship can be found for nondeterministic Turing machines.
Space hierarchy set
The spatial hierarchy theorem states:
The statement is analogous to the time hierarchy theorem. One recognizes, however, that compared to the time already a smaller increase in space is sufficient (factor compared to ) to form a larger class. This also corresponds to an intuitive expectation, as the room as a whole behaves more good-naturedly due to its reusability (old interim results can be overwritten).
What the hierarchy records do not apply to
The hierarchy records relate exclusively to the same calculation mode and a single resource, for example the time resource on a deterministic machine model. However, no statement is made about how space and time classes relate to one another or the relationship between deterministic and nondeterministic classes. However, there are such connections. They are covered in the sections Relationships Between Space and Time Classes and Relationships Between Deterministic and Nondeterministic Classes .
Important time classes
- DTIME (f): General notation for deterministic time classes.
- P : Languages deterministically decidable in polynomial time.
- EXPTIME : Languages that can be determined deterministically in exponential time.
- NTIME (f): General notation for non-deterministic time classes.
- NP : Languages non-deterministically decidable in polynomial time.
- NEXPTIME : Nondeterministically decidable languages in exponential time.
- NC : Functions that can be calculated in parallel in polylogarithmic time.
Important room classes
- DSPACE (f): General notation for deterministic space classes.
- L : Languages deterministically decidable with logarithmically limited space.
- PSPACE : Deterministically decidable languages with polynomial restricted space.
- NSPACE (f): General notation for nondeterministic space classes.
- NL : Nondeterministically decidable languages with logarithmically limited space.
- CSL : Context-sensitive languages are the non-deterministically decidable languages with linearly limited space.
See also: List of complexity classes
Complementation
For each complexity class K, its complement class CoK can be formed: The complement class contains exactly the complements of the elements of the original class. If K is understood as a set of languages ( see power set ), then it is the complement class . In relation to the corresponding decision problems, this means: CoK contains the problems to whose instances the answer is always the opposite of a problem in K.
In contrast to this, one can also consider the complement of a class K. This contains exactly those languages / problems from a given basic set that are not in K; these problems are usually much more severe than those in K. The complement class CoK, on the other hand, usually has a non-empty mean with K.
As a rule, K = CoK applies to deterministic machines, since in the transition function only the transitions to be accepted states have to be replaced by transitions to be rejected states and vice versa. However, this does not apply to other calculation modes, since the acceptance is defined differently here . For example, it is not yet known whether NP = CoNP applies. P = CoP is true, since the underlying model is deterministic and here the accepting and rejecting states in the calculations can simply be exchanged, as mentioned in the previous paragraph. So we immediately see that P is contained in the intersection of NP and CoNP. It is not known whether this average is exactly P.
The P-NP problem and its meaning
One of the most important and still unsolved problems in complexity theory is the P-NP problem . Is class P equal to class NP ? This question can be seen as a central motivation for research in complexity theory, and a large number of the complexity theoretical results were obtained in order to come closer to solving the P-NP problem.
Class P: practically solvable problems
The scope of the P-NP problem results from the experience that the problems of class P are usually practically solvable: Algorithms exist to calculate solutions for these problems efficiently or at least with a reasonable expenditure of time. The time required to solve the problem increases at most polynomially for class P problems . As a rule, algorithms can be found whose time functions are low-degree polynomials . Since the selected machine model of this time class is deterministic (and thus realizable), the problems of class P roughly correspond to the practically solvable problems, even if instances of considerable size are considered.
The class NP: efficiently verifiable problems
The algorithms for solving the problems in NP are based on a nondeterministic machine model . For such machines, unlimited parallelization of the branching calculation paths is assumed, which cannot be technically implemented. The algorithms for solving the problems in NP also work in polynomial time, but on the basis of a physically unrealizable machine model.
As an alternative to the definition via nondeterminism, the class NP can also be described via the verification of problems. In addition to the actual input, a verification algorithm also receives a witness (also called a certificate). For a yes instance, the verification algorithm must come to a positive answer at least from one possible witness. In the case of a no instance, the verification algorithm must not come to a positive answer for any witness. If there is a verification algorithm for a problem that works with a witness of polynomial length in polynomial time, then this problem lies in the class NP. An example of an efficiently verifiable problem is the satisfiability problem (SAT) . The question is asked whether a Boolean formula has an assignment of its variables so that the formula is true. One possible verification algorithm uses a vector as a witness which codes the variable assignment. For a given variable assignment, it is easy to design an efficient algorithm that evaluates the formula for this assignment. So this problem is in class NP. Finding the occupancy is not the task of the verification algorithm.
A nondetermisnistic Turing machine can solve a problem in NP by first generating all possible solutions, whereby the calculation path is branched into a corresponding number of paths, and then verifying each of these solutions, which can be done deterministically, i.e. without further branching.
There are problems in NP that are practically unsolvable for large instances. These include the NP-complete problems. Problems from almost all areas of computer science can be found in this class. But not all problems in NP are difficult, because NP also contains class P.
The case P = NP
If the P-NP problem were solved in the sense of P = NP, we would know that even for NP-complete problems there must be algorithms that work with a polynomial expenditure of time.
Conversely, since the definition of NP-completeness presupposes algorithms with which it is possible to reduce any problems from NP in polynomial time to NP-complete problems, with the polynomial solvability of even a single NP-complete problem, all problems of the class NP would be immediately solvable in polynomial time. This would result in a problem-solving power in the whole of computer science that can not be achieved even with the greatest progress in hardware development.
On the other hand, a solution to the P-NP problem in the sense of P = NP is rather undesirable for certain applications. For example, asymmetrical encryption methods would lose a considerable amount of security, since they could then be broken into polynomial time.
The case P ≠ NP
If the P-NP problem were solved in the sense of P ≠ NP, it would be clear that further efforts to find polynomial solutions for NP-complete problems would be pointless. One can easily imagine that, due to the great importance of the problems in NP, efforts to find an efficient solution are only stopped when it is proven impossible. A lot of private and public research energy will be used up to this point.
In many theorems today, however, it is assumed that P ≠ NP holds, because only in this way can effective research work be carried out without a proof of equality. One looks for ways out through approximations and heuristics, for problem constraints that do not neglect practice.
Consequences for the Complexity Theory
One of the most important research goals of complexity theory is the delimitation of what is practically feasible and thus the field of activity of computer science per se. The previous sections have made the importance of this demarcation clear. In the course of the attempts to solve the P-NP problem, complexity theory brought numerous results to light and gradually refined its analysis methods. These results are used particularly in the design and analysis of practically important algorithms and thus also have a direct effect on practical computer science .
The efforts to solve the P-NP problem, which have been going on for over thirty years, grant the practical computer scientist a high degree of certainty that isolated efforts to efficiently solve problems from NP are more or less pointless. Practical computer science therefore concentrates on approximate solutions or the modification of the original problems when solving problems from NP. For example, the problem complexity of optimization algorithms can be reduced enormously if one does not strive for an optimal solution, but is satisfied with an almost optimal solution. The complexity theory provides the theoretical backing for this approach.
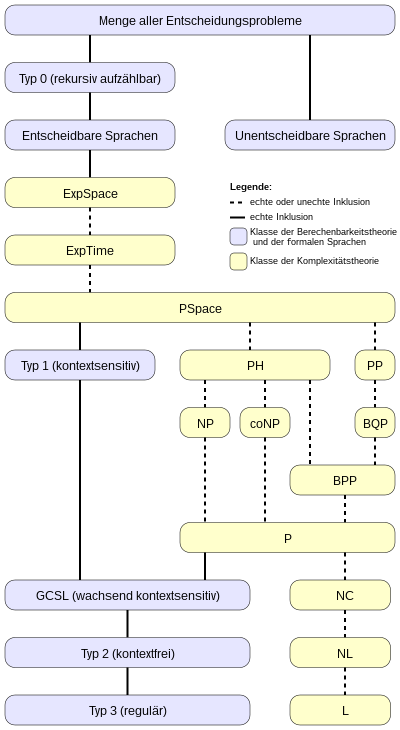
Languages and complexity classes
The following inclusion diagram gives a - quite rough - overview of the relationships between the classes of computability theory , the Chomsky hierarchy and the most important complexity classes .
History of Complexity Theory
After numerous basic terms and important results of complexity theory have been explained in the previous sections, a historical outline is given in the following sections, which should help to classify the chronological order of these results.
Basics
Before the actual start of research explicitly related to the complexity of algorithms, numerous fundamentals were developed. The most important of these is the construction of the Turing machine by Alan Turing in 1936, which turned out to be an extremely flexible model for later algorithm analyzes.
The results of John Myhill (1960), Raymond Smullyan (1961) and Hisao Yamada (1962), who have dealt with special space- and time-limited problem classes, but have not yet started to develop a general theory in their work, are regarded as the first informal complexity-theoretical investigations developed.
Beginning of the complexity theoretical research
Juris Hartmanis and Richard E. Stearns take a first major step towards such a theory in their 1965 work On the computational complexity of algorithms. They already give a quantitative definition of time and space complexity and thus select the two resources that are still considered to be the most important to this day. In doing so, they choose the multi-band Turing machine as the basis and thus make a very robust decision that is valid in many areas of complexity theory. You are also already working on the first hierarchy records.
A number of fundamental results emerged in the following years. In 1967 Manuel Blum published the Speedup theorem . 1969 followed the Union theorem by Edward M. McCreight and Albert R. Meyer. And in 1972 Allan Borodin published the gap theorem. These results can not only be seen as fundamental for the complexity theory, they also represent a sampling of the still new research area, which at the same time has to be justified by the most “spectacular” results possible. So these theorems meet e.g. Sometimes surprising statements, but are sometimes based on assumptions that would be restricted today. For example, no real complexity functions (see above) are required.
In the same period of time, which includes about the first ten years of complexity-theoretical research, class P is formulated as the class of "practically solvable" problems. Alan Cobham shows that the polynomial time is robust under the choice of the machine model (which is summarized today under the extended Church-Turing thesis). In addition, many mathematical functions turn out to be computable in polynomial time.
Exploring the class NP
The class NP first appears with Jack Edmonds, who initially only gives an informal definition. However, the fact that numerous important problems appear to be in NPs soon makes this class an attractive field of research. The concept of reducibility and the NP-completeness based on it is developed and is first expressed succinctly in Cook's theorem (1971): The satisfiability problem (SAT) is NP-complete and thus a most difficult problem in NP. Incidentally, Stephen Cook's original work referred to tautologies ( propositional formulas that are satisfied by each assignment), while the concept of satisfiability is not mentioned. Since the results with regard to the tautologies can be transferred relatively easily to the satisfiability, they are attributed to Stephen Cook. Richard Karp (1972) accomplishes part of this transfer by working out the technique of reduction. Completely independently of this work, Leonid Levin (1973) developed a theory of NP completeness in what was then the Soviet Union , which was ignored in the West for a long time.
In 1979 Michael R. Garey and David S. Johnson published a book describing 300 NP-complete problems ( Computers and intractability ). This book became an important reference for future researchers.
Randomized complexity classes
1982 represents Andrew Yao , the concept of trapdoor functions (trapdoor functions) before that a special type of one-way functions represent (one way functions), and shows their basic importance in the cryptography on. However, for the difficulty of cracking a code, the worst-case approach to complexity classes such as NP is not sufficient. Rather, there must be no algorithms that solve these problems efficiently in a significant proportion of all cases. This corresponds to the model of the probabilistic Turing machine and motivates the introduction of randomized complexity classes such as ZPP , RP or BPP (all introduced by John T. Gill, 1977).
With this overview the essential cornerstones of the history of complexity theory were laid. As in other research areas, the more recent results are divided into many, sometimes very special, sub-areas.
literature
- Sanjeev Arora & Boaz Barak: Computational Complexity. A modern approach . Cambridge University Press, Cambridge 2009, ISBN 978-0-521-42426-4 .
- Ding-Zhu Du & Ker-I Ko: Theory of Computational Complexity. John Wiley & Sons, New York 2000, ISBN 0-471-34506-7 .
- Lance Fortnow & Steve Homer: A Short History of Computational Complexity. November 14, 2002 ( PDF, 225 kB )
- Michael R. Garey & David S. Johnson : Computers and Intractability: A guide to the theory of NP-completeness. Freeman, New York 2003, ISBN 0-7167-1045-5 .
- Juris Hartmanis & Richard E. Stearns : On the computational complexity of algorithms. In: Transactions of the American Mathematical Society. Vol. 117, 1965, pp. 285–306 ( PDF; 2018 KB )
- Jan van Leeuwen (Ed.): Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity. The MIT Press / Elsevier, Amsterdam 1994, ISBN 0-262-72020-5 .
- Christos Papadimitriou : Computational Complexity. Addison-Wesley, Reading / Mass. 1995, ISBN 0-201-53082-1 .
- K. Rüdiger Reischuk: Complexity Theory - Volume I: Fundamentals: machine models , time and space complexity, nondeterminism. 2nd Edition. Teubner, Stuttgart / Leipzig 1999, ISBN 3-519-12275-8 .
- Michael Sipser : Introduction to the Theory of Computation. 2nd Edition. Thomson, Boston 2006, ISBN 0-534-95097-3 . (International Edition)
- Ingo Wegener : Complexity Theory. Limits to the efficiency of algorithms. 1st edition. Springer, Berlin 2003, ISBN 3-540-00161-1 .
Web links
- Complexity Zoo - Directory of the most important complexity classes
Footnotes
- ↑ Such problems exist, for example, in the area of probabilistic complexity classes. If one restricts the error probability here - as is necessary for practically usable probabilistic algorithms - one of the results is that the complexity classes can no longer be enumerated. However, this is a prerequisite for all separation processes. As a result, polynomial time algorithms can suddenly be replaced by linear time algorithms. The example shows how sensitive the network of requirements and the derived sentences is overall.