logarithm

Logarithmic scale graduation of a slide rule (detail)

Graph of the logarithmic function for base 2 (green), e (red) and 1/2 (blue)

In a semi-logarithmic plot (in relation to the x -axis) the graph of the logarithmic function becomes a straight line. Shown here as an example for the logarithm to base 10 .

The logarithm (plural: logarithms; from ancient Greek λόγος lógos , "understanding, doctrine, ratio", and ἀριθμός , arithmós, "number") of a number is the exponent with which a predetermined number, the base, must be raised to the power, to get the given number, the number . Logarithms are only defined for positive real numbers; the base must also be positive.

The logarithm of a positive real number to the base is therefore the value of the exponent when represented as a power to the base , i.e. the number that solves the equation . One writes ; other notations see designations . The logarithms, d. H. the transition from to is thus a reverse operation of exponentiation . The function that assigns its logarithm to every positive number given a fixed base is called the base logarithm function . ${\displaystyle x}$ ${\displaystyle b}$ ${\displaystyle x}$ ${\displaystyle b}$ ${\displaystyle y}$ ${\displaystyle b^{y}=x}$ ${\displaystyle y=\log _{b}(x)}$ ${\displaystyle x}$ ${\displaystyle \log _{b}(x)}$ ${\displaystyle b}$ ${\displaystyle b}$

With logarithms, very rapidly growing series of numbers can be clearly displayed, since the logarithm for large numbers increases much more slowly than the numbers themselves. As the equation shows, you can replace a multiplication with the much less computationally intensive addition by taking logarithms. Logarithms also describe many technical processes and natural phenomena in a mathematically elegant way, such as the behavior of a semiconductor diode , the spiral of a snail shell or the perception of different volume levels by the human ear . ${\displaystyle \log _{b}(x\cdot y)=\log _{b}(x)+\log _{b}(y)}$

Corresponding mathematical calculations have been handed down from India from the time before the birth of Christ . The term logarithm was coined by John Napier in the early 17th century. In honor of Napier, the natural logarithm (see below ) is sometimes also called Napier's logarithm or Nepier's logarithm .

overview

The use of the logarithm can be traced back to Indian antiquity . With the emergence of banking and the advancement of astronomy in 17th century Europe, the logarithm became more and more important. Its function values ​​were recorded in tables, the log tables, so that they could be looked up and not always have to be recalculated. These tables were eventually replaced by slide rules and later by pocket calculators . The switch from tables to slide rules took place in German schools in the 1960s, the switch to pocket calculators from the 1970s.

Central aspects of life can be described with the help of logarithms. For example, the strength of a sensory impression increases depending on a physical quantity such as brightness or volume in accordance with the course of a logarithm function. The same applies to the perceived pitch as a function of the frequency of a tone.

Logarithms acquired their historical significance through context

${\displaystyle \log(xy)=\log x+\log y,}$

which allows a multiplication to be expressed by an addition .

Formally, logarithms are all solutions to the equation ${\displaystyle x}$

${\displaystyle a=b^{x}}$

to given sizes and . ${\displaystyle a}$ ${\displaystyle b}$

Depending on which number range and for which quantities this equation is considered, it has no, several or exactly one solution. If the solution is unique, then it is called the logarithm from to the base ${\displaystyle a}$ ${\displaystyle b}$ and one writes

${\displaystyle x=\log _{b}a}$

For example, the logarithm of 8 to base 2 is 3, written because it is . ${\displaystyle \log _{2}8=3}$ ${\displaystyle 2^{3}=8}$

If the above equation to be dissolved rather than after , the solution is given by the -th root of . ${\displaystyle b}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle a}$

The best known and most widespread is the logarithm over the positive real numbers , which is mainly shown in the following.

history

Title page to Jost Bürgi's logarithmic table from 1620

Indian mathematicians in the 2nd century BC Were the first to mention logarithms. Even in ancient times , they used base 2 logarithms for their calculations. In the 8th century, the Indian mathematician Virasena described base 3 and 4 logarithms. From the 13th century onwards, Arabic mathematicians created entire logarithmic tables.

Nicolas Chuquet clearly worked out the arithmetic laws for powers and out through a juxtaposing arrangement of an arithmetic and a geometric series. ${\displaystyle a^{n}\cdot a^{m}=a^{n+m}}$ ${\displaystyle (a^{n})^{m}=a^{n\cdot m}}$

The German mathematician Michael Stifel formulated the relationships similarly in 1544 and alongside other authors of the 16th century. The reduction from multiplication to addition stands next to trigonometric addition formulas at the beginning of the development of the logarithms. Stifel only allowed whole number exponents. John Napier's (1550–1617) idea, however, was to allow a continuous range of values ​​for the exponents. ${\displaystyle q^{m}\cdot q^{n}=q^{m+n}}$ ${\displaystyle {\tfrac {q^{m}}{q^{n}}}=q^{m-n}}$

In the 17th century, the Swiss watchmaker Jost Bürgi (1552–1632) developed a new system for calculating logarithms, which he published in 1620 after a long period of work. But even before that, in 1614, the Scottish thinker John Napier published a book on logarithms that made him famous as the "inventor of logarithms". However, Bürgi and Napier developed their work and knowledge of logarithms independently of one another.

The Greek word "logarithm" means "ratio" in German and comes from Napier. The following applies: Exactly then, to is in the same relationship as to (as a formula :) if the differences in their logarithms match (as a formula:) . Logarithms of this were first published under the title Mirifici logarithmorum canonis descriptio, which can be translated as a description of the wonderful canon of logarithms . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$ ${\displaystyle d}$ ${\displaystyle a:b=c:d}$ ${\displaystyle \log(a)-\log(b)=\log(c)-\log(d)}$

After the Oxford professor Henry Briggs (1561-1630) had dealt intensively with this font, he contacted its author and suggested using base 10 for the logarithms (abbreviated lg). These spread quickly and were particularly valued in astronomy, which Pierre-Simon Laplace also found in comparison with the previously used trigonometric tables:

"L'invention des logarithmes, en réduisant le temps passé aux calculs de quelques mois à quelques jours, double pour ainsi dire la vie des astronomes."

"By reducing the time needed for calculations from a few months to a few days, the invention of logarithms doubled the lifespan of an astronomer, so to speak."

If Euler's number  - which was determined by Leonhard Euler (1707–1783) in 1728 and published for the first time in 1742 - is used as the basis of the logarithm, it is called the natural logarithm. The natural logarithm is abbreviated by "ln". ${\displaystyle \mathrm {e} }$

The logarithms laid the mathematical basis for the further development of the mechanical slide rule ; because the function of the slide rule is based on the principle of addition and subtraction of logarithms.

Logarithm in application and nature

The case of a Nautilus shows a logarithmic spiral

A logarithmic spiral

A slide rule

There are many applications of the logarithm in science when the range of values encompasses many orders of magnitude . Data are either represented on a logarithmic scale , or logarithmically defined quantities are used, such as the pH value or the sensitivity of the sensory organs .

In the living nature

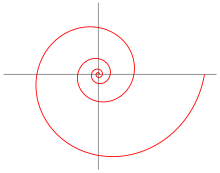
In living nature there are numerous examples of logarithmic spirals , e.g. B. the growth of snail shells or the arrangement of the kernels on the sunflower .

Sound pressure level

The sound pressure level is used as a logarithmic measure to describe the strength of a sound event. The auxiliary unit of measurement decibel (dB) is used for this.

Sensation of brightness

A logarithmic evaluation has also proven itself for the sensory perception of brightness ( Weber-Fechner law ), since the human eye can bridge up to 10.5 powers of ten in physical luminance between twilight and bright sunshine.

PH value

The pH value is the measure of the acidic or basic character of an aqueous solution. Note: In chemistry, logarithmic scales are generally identified by a preceding p (for power), for example for pKs or pKb values.

Richter scale

The Richter scale, which is used to describe earthquake strengths, is based on a decal-logarithmic scale. The earthquake strength therefore increases exponentially from level to level.

Star brightness

Star brightnesses are given in astronomical size classes , which represent a logarithmic measure of the actual radiation intensity.

Slide rule

Before electronic calculators were available, we used the Logarithmengesetze out to multiplications to additions and divisions to subtractions to simplify. The calculation of the square root is simplified at the level of the logarithm to a division by two. Because the logarithm itself is not that easy to calculate, slide rules with their logarithmic graduations and logarithm tables were widely used aids.

Growth and Decay Processes

Typical tasks in growth and decay processes can be modeled using the inverse function of the logarithm - the exponential function. See exponential process , absorption .

Number of digits in a number

Calculation of the number of digits required to represent a natural number in a place value system. To represent a natural number as a base , digits are required. The brackets mean rounding off to the next whole number that is less than or equal to. ${\displaystyle n}$ ${\displaystyle b}$ ${\displaystyle 1+\lfloor \log _{b}n\rfloor }$

For example is . The above formula gives the value 7. So you need 7 digits to represent 100 in the dual system, namely . If, on the other hand, you represent 100 in the hexadecimal system, you need two digits, because . It is . ${\displaystyle \log _{2}100\approx 6{,}64}$ ${\displaystyle 100=1100100_{2}}$ ${\displaystyle \log _{16}100\approx 1{,}66}$ ${\displaystyle 100=64_{16}}$

Benford's law

The distribution of the digits of numbers in empirical data sets, for example their first digits, follows a logarithmic distribution, Benford's law .

Information unit

Measurement of the amount of information ; The information theory says that when something likely to occur, the knowledge about the actual occurrence of which an amount of information of bit follows. For example, the “heads” result of a fair coin toss ( ) gives the amount of information bit, and one bit is enough to encode this information . ${\displaystyle p}$ ${\displaystyle \log _{2}{\tfrac {1}{p}}}$ ${\displaystyle p=0{,}5}$ ${\displaystyle \log _{2}2=1}$

Cryptography

The discrete logarithm in finite bodies and elliptic curves defined on them is considerably more complex to calculate than its inverse function, the discrete exponential function . The latter can therefore be used as a so - called one - way function in cryptography for encryption .

Logarithmic time scales

Logarithmic time scales can be found in the history of technology as well as in the geological time scale .

Intervals of music theory

Intervals have an exponential frequency curve. However, the hearing perceives this as linear. The proportions are therefore given as logarithms. The octave is divided into 1200 cents (music) . Example:

interval	Frequency ratio	size
1 octave	2	1200 cents
2 octaves	4th	2400 cents
3 octaves	8th	3600 cents
...
major third	5: 4	${\displaystyle 1200\cdot \log _{2}{\big (}{\tfrac {5}{4}}{\big )}\,{\text{Cent}}=386{,}314\,{\text{Cent}}}$
Fifth	3: 2	${\displaystyle 1200\cdot \log _{2}{\big (}{\tfrac {3}{2}}{\big )}\,{\text{Cent}}=701{,}955\,{\text{Cent}}}$

Graphical representation of functions

For the graphical representation of functions, special mathematical papers are used, such as single-logarithmic paper or double-logarithmic paper .

Designations

One writes for the logarithm from to the base ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle x=\log _{b}a}$

and says: " is the logarithm from to the base " ${\displaystyle x}$ ${\displaystyle a}$ ${\displaystyle b}$ . is called number or obsolete logarithm. The result of taking the logarithm indicates the exponent to which the base has to be raised in order to obtain the number . ${\displaystyle a}$ ${\displaystyle x}$ ${\displaystyle b}$ ${\displaystyle a}$

The term characteristic (sometimes also a key figure ) is usually used for the places before the decimal point of the logarithm ; its places after the decimal point are called the mantissa .

Controls on a calculator. The key LOGrepresents the logarithm for base 10, LNregardless of the manufacturer, and calculates the natural logarithm for base e . In addition, the corresponding inverse function is provided as the second assignment of the respective keys (yellow lettering above), the exponential function for base 10 or e.

${\displaystyle \operatorname {log} _{b}a}$

The general mathematical symbol for the logarithm according to DIN 1302 . It is more rare to find spellings that differ from this, such as . ${\displaystyle {}_{b}\,\!\log a}$

${\displaystyle \operatorname {log} a}$

The symbol without a specified basis is used if the basis used is irrelevant, if it is agreed separately, is evident from the context or is determined on the basis of a convention. In technical applications (e.g. on most pocket calculators) it often stands for the decadic logarithm. In theoretical treatises, especially on number theory topics , often stands for the natural logarithm. ${\displaystyle \log }$ ${\displaystyle \log }$ ${\displaystyle \log }$

In addition, special notations are specified for the logarithm in DIN 1302, depending on the application:

${\displaystyle \operatorname {ln} a}$

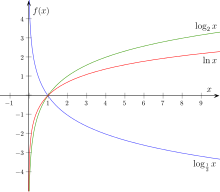
Natural logarithm ( Latin logarithmus naturalis ), the base logarithm, Euler's number 2.7182818 ... It is used in connection with exponential functions . ${\displaystyle \mathrm {e} }$

${\displaystyle \operatorname {lg} a}$

Decadic logarithm , also known as logarithm of ten or Briggs' logarithm , the logarithm to the base 10. It is used in numerical calculations in the decimal system.

${\displaystyle \operatorname {lb} a}$

Binary logarithm, also known as logarithm of two , the logarithm for base 2. It is used in computer science for calculations in the binary system. Outside of the norm -  logarithm dualis  - is also used with the same meaning . ${\displaystyle \operatorname {ld} a}$

A function symbol that looks similar is for the integral logarithm . However, this function is not a logarithmic function. ${\displaystyle \operatorname {li} a}$

definition

The logarithm can always be understood mathematically as a family of functions (the parameters of which are denoted by) of . Their individual logarithmic functions are only different (real, but not equal to zero) multiples of each other. ${\displaystyle b}$ ${\displaystyle \mathbb {R} ^{+}\to \mathbb {R} }$

It can be introduced in different ways over the positive real numbers. Depending on the background and intention, you will choose one or the other didactic approach. The different definitions of the real logarithm are equivalent to one another and are made here with a special focus on the natural logarithm, which occurs naturally from the mathematician's point of view , as can be seen with the approach using the antiderivative of . ${\displaystyle {\tfrac {1}{t}}}$

As the inverse function of the exponential function

The logarithm to the base  is the inverse function of the general exponential function to the positive base : ${\displaystyle b}$ ${\displaystyle b}$

${\displaystyle x\mapsto b^{x}.}$

The functions and are therefore inverse functions of one another, i.e. H. Logarithmizing reverses exponentiation and vice versa: ${\displaystyle b^{x}}$ ${\displaystyle \log _{b}x}$

${\displaystyle b^{\log _{b}x}=x\quad {\text{und}}\quad \log _{b}(b^{x})=x.}$

The natural logarithm results from the base , where ${\displaystyle b=\mathrm {e} }$

${\displaystyle \mathrm {e} =2{,}718281828459\ldots }$

is Euler's number .

As a solution to a functional equation

The logarithmic functions are the non-trivial, continuous solutions of the functional equation ${\displaystyle L}$

${\displaystyle L(x\cdot y)=L(x)+L(y).}$

Your solutions always fulfill and even prove to be differentiable. The natural logarithm is then obtained together with the additional condition ${\displaystyle L(1)=0}$

${\displaystyle L'(1)=1.}$

The additional condition is one of the reasons for calling the resulting logarithm natural . If you wanted to get the logarithm for a different basis  via the additional condition, then you would have to ${\displaystyle b}$

${\displaystyle L'(1)={\frac {1}{\ln b}}}$

and would need the natural logarithm again.

The trivial solution of the above functional equation is the null function , which is not regarded as a logarithmic function, and the only solution of the functional equation for which is also defined. ${\displaystyle L(x)=0}$ ${\displaystyle L(0)}$

Due to the above functional equation, the logarithm therefore conveys in particular a structure-preserving mapping from the positive real numbers with their multiplicative structure to the entire real numbers with their additive structure. One can also explicitly demand this as a condition and thus arrive at the derivation.

As an isomorphism

The real-valued logarithms are exactly the continuous isomorphisms

${\displaystyle L\colon (\mathbb {R} ^{+}\!,\,\cdot \,)\longrightarrow (\mathbb {R} ,+)}$.

This definition clearly defines the function except for a multiplicative constant. ${\displaystyle L}$

The algebraic approach, like the approach via the functional equation, emphasizes the historical importance of the logarithm as a calculation aid: It enables a multiplication to be “converted” into an addition.

As an antiderivative of f with f ( x ) = 1 / x

The natural logarithm as the area under the graph of 1 / x

The function

${\displaystyle L\colon t\mapsto \int _{1}^{t}{\frac {1}{x}}\,\mathrm {d} x}$

with is just the natural logarithm: It is . The logarithm with the base is  obtained by dividing the function  by the constant . Considered as an improper integral of , or any arbitrary (positive) lower integration limit, one would only get an additional, additive constant, but only ever get the logarithm as the base . ${\displaystyle t>0}$ ${\displaystyle L=\ln }$ ${\displaystyle b}$ ${\displaystyle L}$ ${\displaystyle L(b)=\ln b}$ ${\displaystyle f}$ ${\displaystyle \mathrm {e} }$

As a power series

The natural logarithm can be used as a power series according to

${\displaystyle \ln(1+x)=\sum _{k=1}^{\infty }(-1)^{k+1}{\frac {x^{k}}{k}}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dotsb }$

be introduced. This series converges for and for . ${\displaystyle |x|<1}$ ${\displaystyle x=1}$

The relationship is useful for numerical calculation of the value for . ${\displaystyle \ln(1+x)}$ ${\displaystyle x>1}$ ${\displaystyle \ln(1+x)=-\ln {\Bigl (}1+{\Bigl (}-{\frac {x}{1+x}}{\Bigr )}{\Bigr )}}$

annotation

These definitions can also be used to get logarithms on other mathematical structures, such as B. on the complex numbers. This assumes that the concepts used for the definition exist in the relevant structure.

For example, to define the discrete logarithm on a group , concepts such as differentiation / integration cannot be used because they do not exist there. (The definition takes place there as the inversion of the exponentiation with whole exponents, which in turn is defined from multiple use of one link in the group.)

Calculation rules and basic properties

Logarithmic Laws

In the following it is always assumed that the variables are different from zero; in the case of the real logarithm, the numbers are even assumed to be positive. The bases of the logarithm must also not be 1. ${\displaystyle x,y,x_{i},r,a,b}$ ${\displaystyle a,b}$

Products

There is a helpful rule for calculating with logarithms of products

${\displaystyle \log _{b}(x\cdot y)=\log _{b}x+\log _{b}y}$

to disposal; or more generally:

${\displaystyle \log _{b}(x_{1}x_{2}\dotsm x_{n})=\log _{b}x_{1}+\log _{b}x_{2}+\dotsb +\log _{b}x_{n}}$

or.

${\displaystyle \log _{b}\prod _{i=1}^{n}x_{i}=\sum _{i=1}^{n}\log _{b}x_{i}.}$

The logarithm of a product is the sum of the logarithms of the factors.

Quotient

The quotients are derived directly from the logarithms of products. Here is just the simple case

${\displaystyle \log _{b}{\frac {x}{y}}=\log _{b}x-\log _{b}y}$

specified. The logarithm of a quotient is the logarithm of the numerator minus the logarithm of the denominator . ${\displaystyle x}$ ${\displaystyle y}$

In particular, this results in : ${\displaystyle \log 1=0}$

${\displaystyle \log _{b}{\frac {1}{x}}=-\log _{b}x}$

More generally, the reciprocity law results directly from the above quotient rule:

${\displaystyle \log _{b}{\frac {x}{y}}=-\log _{b}{\frac {y}{x}}}$

Sums and differences

A formula for logarithms of sums (and differences) can be derived from the formula for products , by excluding: ${\displaystyle x+y}$ ${\displaystyle x}$

${\displaystyle x+y=x\left(1+{\frac {y}{x}}\right).}$

This results in the "rule"

${\displaystyle \log _{b}(x+y)=\log _{b}x+\log _{b}\left(1+{\frac {y}{x}}\right).}$

Potencies

The rule applies to powers with a real exponent ${\displaystyle r}$

${\displaystyle \log _{b}\left(x^{r}\right)=r\log _{b}x.}$

The logarithm of a power is therefore the product of the exponent with the logarithm of the base.

This can also be used for ${\displaystyle r=-1}$

${\displaystyle \log _{b}{\frac {1}{x}}=-\log _{b}x}$

determine.

The logarithm of a fraction is the negative logarithm of the denominator . ${\displaystyle {\tfrac {1}{x}}}$ ${\displaystyle x}$

These calculation rules can be derived from the power laws .

root

Since roots are nothing more than powers with a broken exponent, the rule of calculation results from the power rule of the logarithm given above

${\displaystyle \log _{b}{\sqrt[{n}]{x}}=\log _{b}\left(x^{\frac {1}{n}}\right)={\frac {1}{n}}\log _{b}x.}$

Base conversion

To calculate base logarithms using logarithms of any base , use the relationship ${\displaystyle b}$ ${\displaystyle a}$

${\displaystyle \log _{b}x={\frac {\log _{a}x}{\log _{a}b}}}$

because the transformations also apply ${\displaystyle y=\log _{b}x}$

${\displaystyle {\begin{aligned}b^{y}&=x\\\log _{a}b^{y}&=\log _{a}x\\y\log _{a}b&=\log _{a}x\\y&={\frac {\log _{a}x}{\log _{a}b}}\end{aligned}}}$

This shows that logarithms for different bases only differ from one another by a constant factor. Most tables only provide logarithms for base 10, pocket calculators also for base e (the natural logarithm). The above formula can be used to calculate logarithms on any basis.

A prominent special case that results from the above formula is:

${\displaystyle \log _{a}b={\frac {1}{\log _{b}a}}}$ or ${\displaystyle \log _{a}b\cdot \log _{b}a=1}$

example

${\displaystyle \log _{10}8={\frac {\log _{2}8}{\log _{2}10}}={\frac {\ln 8}{\ln 10}}}$

for any positive numbers is ${\displaystyle x}$ ${\displaystyle {\frac {\ln x}{\log _{10}x}}=\ln 10\approx 2{,}302585}$

Non-positive numbers

In the real numbers , the logarithm for non-positive numbers, i.e. zero and negative numbers , is not defined. However, the above functional equation holds for as long as is, since it has a point of discontinuity there. Otherwise, yes for all would always follow if one were to demand their validity for the whole , i.e. also for . ${\displaystyle \log _{b}|x|}$ ${\displaystyle L(\cdot )}$ ${\displaystyle x,y\not =0}$ ${\displaystyle x=0}$ ${\displaystyle y}$ ${\displaystyle 0=L(y)}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle x=0}$

• ${\displaystyle x=\log _{b}0}$should mean then . If it is not equal to zero, this cannot be solved for any real one . ${\displaystyle 0=b^{x}}$ ${\displaystyle b}$ ${\displaystyle x}$
• (as an example the negative number −1) should then mean. This is also not possible for a real number if it is greater than zero. ${\displaystyle x=\log _{b}(-1)}$ ${\displaystyle -1=b^{x}}$ ${\displaystyle x}$ ${\displaystyle b}$

In function theory , in which functions of complex numbers are considered, the logarithm can also be defined for negative numbers (see complex logarithm ), although some of the calculation rules no longer apply. In this context, too, 0 is not an isolated singularity , but a branch point .

Derivative and integral

The natural logarithm function is the inverse of the exponential function . Therefore the derivative of the natural logarithm can be obtained simply by applying the inverse rule (see example there ). It turns out

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\ln(x)={\frac {1}{x}}}$

for positive . ${\displaystyle x}$For negative it ${\displaystyle x}$ follows (because of and using the chain rule ) ${\displaystyle -x>0}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\ln(-x)={\frac {1}{-x}}\cdot (-1)={\frac {1}{x}}}$

and because of that, both are allowed ${\displaystyle |x|={\begin{cases}x,&{\text{für }}x>0\\-x,&{\text{für }}x<0\end{cases}}}$

${\displaystyle \forall \ x\neq 0\colon {\frac {\mathrm {d} }{\mathrm {d} x}}\ln |x|={\frac {1}{x}}}$

sum up. The following applies to general logarithms:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\log _{b}|x|={\frac {1}{x\ln b}}.}$

For all real is ${\displaystyle x\neq 0}$

${\displaystyle \int _{-1}^{x}{{\frac {1}{t}}\,\mathrm {d} t}=\ln |x|,}$

where the main value of the integral is to be taken for positive (i.e. when integrated over the pole at ) . ${\displaystyle x}$ ${\displaystyle t=0}$

The antiderivative (also known as the indefinite integral ) of the natural logarithm can be obtained through partial integration :

${\displaystyle {\begin{aligned}\int {\ln |x|\,\mathrm {d} x}&=\int 1\cdot \ln |x|\,\mathrm {d} x\\&=\int {\frac {\mathrm {d} }{\mathrm {d} x}}x\cdot \ln |x|\,\mathrm {d} x\\&=x\ln |x|-\int x{\frac {1}{x}}\,\mathrm {d} x\\&=x\ln |x|\;-x+C.\end{aligned}}}$

If one of the limits is zero for a certain integral of the natural logarithm, then de l'Hospital's rule can be applied.

example

${\displaystyle \int _{0}^{1}{\ln x\,\mathrm {d} x}=[x\ln {x}-x]_{0}^{1}=-1,}$

there

${\displaystyle {\begin{aligned}\lim _{x\to 0^{+}}x\ln x&=\lim _{x\to 0^{+}}{\frac {\ln x}{1/x}}\\&=\lim _{x\to 0^{+}}{\frac {1/x}{-1/x^{2}}}\\&=\lim _{x\to 0^{+}}-x\\&=0.\end{aligned}}}$

Curve discussion

• Definition set : ${\displaystyle \mathbb {R} ^{+}={\mathopen {]}}0,\infty {\mathclose {[}}}$
• Set of values : ${\displaystyle \mathbb {R} }$
• Set of zeros or curve intersections with the coordinate axes : {1} or (1 | 0)
• Asymptotic behavior :

${\displaystyle \lim _{x\to 0^{+}}\log _{b}x={\begin{cases}-\infty ,&{\text{wenn }}b>1\\+\infty ,&{\text{wenn }}b<1\end{cases}}}$

${\displaystyle \lim _{x\to \infty }\log _{b}x={\begin{cases}+\infty ,&{\text{wenn }}b>1\\-\infty ,&{\text{wenn }}b<1\end{cases}}}$

• First derivative :

${\displaystyle (\log _{b}|x|)'={\frac {1}{x\ln b}}}$

• Extreme points : none
• Turning points : none
• Monotony : strictly monotonously increasing / increasing (if ) or decreasing (if ) ${\displaystyle b>1}$ ${\displaystyle b<1}$
• Area of the area between curve, y-axis and x-axis up to x ≤ 1: ${\displaystyle {\frac {1}{|\ln b|}}}$
• Extremum of curvature at with ${\displaystyle x_{k}={\frac {1}{{\sqrt {2}}|\ln b|}}}$ ${\displaystyle \kappa (x_{k})=-{\frac {2\ln b}{3{\sqrt {3}}}}}$

Natural logarithm

The logarithm to the base ( Euler's number ) is also known as the natural logarithm and is abbreviated with "ln" or often also "log" (without subscript ): ${\displaystyle \mathrm {e} }$

If so then is ${\displaystyle y=\mathrm {e} ^{x}}$ ${\displaystyle x=\log _{\mathrm {e} }y=\ln y}$

- or put more simply: ${\displaystyle \ln(\mathrm {e} ^{x})=x}$

The number is e.g. B. distinguished (and could also be defined) that the exponential function reproduces itself when derived from , as a formula: ${\displaystyle \mathrm {e} }$ ${\displaystyle \mathrm {e} ^{x}}$ ${\displaystyle x}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {e} ^{x}=\mathrm {e} ^{x}.}$

The term natural logarithm was chosen because both the exponential function and the base logarithm occur naturally in many contexts ( integral calculus , differential calculus , complex numbers , trigonometry ) without pre-factors. In particular, the natural logarithm can be integrated and differentiated very easily. ${\displaystyle \mathrm {e} }$

The natural logarithm is an antiderivative of the reciprocal function with , namely exactly with . ${\displaystyle \ln }$ ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle f(x)=x^{-1}={\tfrac {1}{x}}}$ ${\displaystyle F(1)=0}$

Calculating the logarithm

The calculation of a logarithm is complicated in principle. It can only be achieved “with paper and pencil” by repeating certain arithmetic operations many times, using the result of the step just carried out as the starting point for the next calculation step ( iterative procedure ). Usually one can only approximate the value ( approximation ) . There are several possible ways to do this, some of which are shown below. Initially, the result of these partial steps is in each case relatively far removed from the correct result, but becomes more precise with each further calculation step, and it converges to the correct result. Such iterative arithmetic operations are very well suited to be carried out automatically with a pocket calculator or computer , where only a key has to be pressed (if provided on the device) to convert the logarithm of the entered number to a fixed base (usually the Euler number e ( 2.718 ...) or the number 10). The following calculation examples are only suitable for calculating the logarithm of any number based on e (natural logarithm) or 2.

Power series

Illustration of the first partial sums of the series representation of the natural logarithm discovered by Nikolaus Mercator ; the series only converges in the non-hatched area

The power series expansion of the natural logarithm around the expansion point 1 results for as ${\displaystyle -1<x\leq 1}$

${\displaystyle {\begin{aligned}\ln(1+x)&=-\sum _{k=0}^{\infty }{\frac {(-x)^{k+1}}{k+1}}\\&=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}\pm \dotsb \\&\qquad \dotsb +(-1)^{n+1}{\frac {x^{n}}{n}}\;+\;R_{n+1}(x)\,.\end{aligned}}}$

It does not converge particularly quickly at the edges of the convergence interval, the remainder of the -th partial sum has the size ${\displaystyle n}$

${\displaystyle |R_{n+1}(x)|\leq {\frac {|x|^{n+1}}{(n+1)(1-|x|)}}.}$

This series can also be represented as a continued fraction :

${\displaystyle \ln(1+x)={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+\ddots }}}}}}}}}$

With the help of the formula one can reduce the calculation of the logarithm for any to that for values ​​in the interval , i. i.e., one always finds and with and ${\displaystyle \ln(x)=m\ln(2)+\ln(2^{-m}x)}$ ${\displaystyle x}$ ${\displaystyle {\big [}{\tfrac {2}{3}},{\tfrac {4}{3}}{\big ]}}$ ${\displaystyle m}$ ${\displaystyle y}$ ${\displaystyle 2^{-m}x=1+y}$ ${\displaystyle |y|\leq {\tfrac {1}{3}}}$

Illustration of the convergence of the adjacent artanh development for different numbers of summands

The following series display , which is based on the power series expansion of the hyperbolic areatangent,   offers more flexibility in the reduction to numbers close to 1 and halving the calculation effort   . ${\displaystyle \operatorname {artanh} }$

${\displaystyle {\begin{aligned}\ln x&=2\operatorname {artanh} {\frac {x-1}{x+1}}\\&=\sum _{k=0}^{\infty }{\frac {2}{2k+1}}\cdot \left({\frac {x-1}{x+1}}\right)^{2k+1}\\&=\sum _{k=0}^{n}{\frac {2}{2k+1}}\cdot \left({\frac {x-1}{x+1}}\right)^{2k+1}\!\!+\,\,R_{n+1}(x)\end{aligned}}}$

with the remaining term estimate

${\displaystyle |R_{n+1}(x)|\leq {\frac {(x-1)^{2}}{2(2n+3)\,|x|}}\left|{\frac {x-1}{x+1}}\right|^{2n+1}.}$

The series converges for , shows similar convergence behavior for and and converges better the closer it is to 1. To do this, one uses again ${\displaystyle x>0}$ ${\displaystyle x}$ ${\displaystyle {\tfrac {1}{x}}}$ ${\displaystyle x}$

${\displaystyle \ln x=2m\ln({\sqrt {2}})+\ln(2^{-m}x).}$

By choosing a suitable whole number , one can always achieve that, and thus increase the speed of convergence of the series that is now calculated for. However, you also have to calculate an approximation for what happens over the same series. Such a transformation to an interval by scaling with is also possible for other values ​​of ; due to the particularly simple handling of the 2 numbers represented in binary, another factor is rarely used. ${\displaystyle m}$ ${\displaystyle {\tfrac {1}{\sqrt {2}}}\leq 2^{-m}x\leq {\sqrt {2}}}$ ${\displaystyle 2^{-m}x}$ ${\displaystyle \ln {\sqrt {2}}={\tfrac {1}{2}}\ln 2}$ ${\displaystyle {\big [}{\tfrac {1}{b}},b{\big ]}}$ ${\displaystyle x}$ ${\displaystyle b^{2m}}$ ${\displaystyle b}$

Additive decomposition

As   mentioned in the section above, the natural logarithm   is associated with the hyperbolic areatangent   per ${\displaystyle \ln }$   ${\displaystyle \operatorname {artanh} }$

${\displaystyle \ln x=2\operatorname {artanh} {\frac {x-1}{x+1}}\qquad \,(0<x)}$

in relationship to what is dissolved after the other

${\displaystyle \operatorname {artanh} u={\frac {1}{2}}\ln {\frac {1+u}{1-u}}\qquad (-1<u<1)}$

results.

The logarithms of the positive-integer numbers can thus be in ascending units of the form

${\displaystyle {\begin{aligned}\ln(n+1)&=\ln n+\ln {\frac {n+1}{n}}=\ln n+2\operatorname {artanh} {\frac {1}{2n+1}}\\&=2\sum _{\nu =1}^{n}\operatorname {artanh} {\frac {1}{2\nu +1}}\end{aligned}}}$

represent and calculate. The convergence behavior of the Taylor series improves

${\displaystyle \operatorname {artanh} u=\sum _{k=0}^{\infty }{\frac {u^{2k+1}}{2k+1}}=u+{\frac {1}{3}}u^{3}+{\frac {1}{5}}u^{5}+{\frac {1}{7}}u^{7}+\ldots }$

slightly with increasing ${\displaystyle n.}$

Using the addition theorem

${\displaystyle \operatorname {artanh} u+\operatorname {artanh} v=\operatorname {artanh} {\frac {u+v}{1+uv}}}$

can be     broken down   and thus also   additively. For example, the following identities result for the natural logarithms of the first prime numbers. For the sake of clarity, the addition theorem is used as a group law ${\displaystyle \operatorname {artanh} }$ ${\displaystyle \ln }$ ${\displaystyle \oplus }$

${\displaystyle u\oplus v:=\tanh(\operatorname {artanh} u+\operatorname {artanh} v)={\frac {u+v}{1+uv}},}$

as well as its multiple reproduction as ${\displaystyle n}$

${\displaystyle n\!\odot \!u:=\underbrace {u\oplus u\oplus \dotsb \oplus u} _{n{\text{-mal}}}=\bigoplus _{\nu =1}^{n}u}$

formulated.

${\displaystyle \tanh \left({\tfrac {1}{2}}\ln 2\right)}$	${\displaystyle ={\tfrac {1}{3}}}$	${\displaystyle =2\!\odot \!{\tfrac {1}{7}}\;\oplus \;{\tfrac {1}{17}}}$	${\displaystyle =\;\,7\!\odot \!{\tfrac {1}{19}}\;\ominus \;\;\,2\!\odot \!{\tfrac {1}{49}}\;\oplus \;3\!\odot \!{\tfrac {1}{161}},}$
${\displaystyle \tanh \left({\tfrac {1}{2}}\ln 3\right)}$	${\displaystyle ={\tfrac {1}{2}}}$	${\displaystyle =3\!\odot \!{\tfrac {1}{7}}\;\oplus \;2\!\odot \!{\tfrac {1}{17}}}$	${\displaystyle =11\!\odot \!{\tfrac {1}{31}}\;\oplus \;\;\,8\!\odot \!{\tfrac {1}{49}}\;\oplus \;5\!\odot \!{\tfrac {1}{161}},}$
${\displaystyle \tanh \left({\tfrac {1}{2}}\ln 5\right)}$	${\displaystyle ={\tfrac {2}{3}}}$	${\displaystyle =4\!\odot \!{\tfrac {1}{5}}\;\ominus \;{\tfrac {1}{161}}}$	${\displaystyle =16\!\odot \!{\tfrac {1}{31}}\;\oplus \;12\!\odot \!{\tfrac {1}{49}}\;\oplus \;7\!\odot \!{\tfrac {1}{161}},}$
${\displaystyle \tanh \left({\tfrac {1}{2}}\ln 7\right)}$	${\displaystyle ={\tfrac {3}{4}}}$	${\displaystyle =3\!\odot \!{\tfrac {1}{3}}\;\ominus \;{\tfrac {1}{15}}}$	${\displaystyle =14\!\odot \!{\tfrac {1}{15}}\;\oplus \;\;\,6\!\odot \!{\tfrac {1}{97}}\;\ominus \;3\!\odot \!{\tfrac {1}{127}}}$     such as
${\displaystyle \tanh \left({\tfrac {1}{2}}\ln 11\right)}$	${\displaystyle ={\tfrac {5}{6}}}$	${\displaystyle =2\!\odot \!{\tfrac {1}{2}}\;\oplus \;{\tfrac {1}{10}}}$	${\displaystyle =24\!\odot \!{\tfrac {1}{23}}\;\oplus \;11\!\odot \!{\tfrac {1}{65}}\;\ominus \;7\!\odot \!{\tfrac {1}{485}}.}$

For practical purposes, decompositions are preferred whose summands have a one in the numerator. As with the arctangent, stay with the doubling

${\displaystyle {\tfrac {1}{n}}=2\!\odot \!{\tfrac {1}{2n}}\;\oplus \;{\tfrac {1}{4n^{3}-3n}}}$

get the ones in the numerator.

Limit values ​​according to Hurwitz

The limit values ​​apply to the natural logarithm

${\displaystyle \ln x=\lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)}$

as well as synonymous with it

${\displaystyle \ln x=\lim _{h\to 0}{\frac {x^{h}-1}{h}}=\lim _{h\to 0}\int _{1}^{x}{\frac {1}{t^{1-h}}}\,\mathrm {d} t}$

which is easily confirmed by the de l'Hospital rule .

The limit values ​​specified by Adolf Hurwitz for the natural logarithm of the sequences or those over ${\displaystyle a_{n}}$ ${\displaystyle b_{n}}$

${\displaystyle {\begin{aligned}a_{n}&=2^{n}(x_{n}-1)\\b_{n}&=2^{n}\left(1-{\frac {1}{x_{n}}}\right),\end{aligned}}}$

in which

${\displaystyle x_{n+1}={\sqrt {x_{n}}}\quad {\text{mit}}\quad x_{0}=x}$

are defined. Because of and because is monotonically decreasing and monotonically increasing, the convergence of these two sequences follows. Due to and , the two limit values ​​are equal: ${\displaystyle 1-{\tfrac {1}{x}}\leq b_{n}\leq a_{n}<x-1}$ ${\displaystyle a_{n}}$ ${\displaystyle b_{n}}$ ${\displaystyle a_{n}=b_{n}x_{n}}$ ${\displaystyle x_{n}\rightarrow 1}$

${\displaystyle \lim _{n\to \infty }a_{n}=\lim _{n\to \infty }b_{n}=\ln x.}$

However, because of the extinction that occurs, these limit values are not well suited for a practical calculation of ln . ${\displaystyle x}$

Calculation of single binary digits

Another possibility for calculating the logarithm is to determine the digits of the binary representation of the logarithm for base 2 one after the other. This method is particularly easy to implement on arithmetic units because it avoids time-consuming divisions and can also be easily converted into fixed-point arithmetic .

First, the decimal logarithm of the are (always in the Dual System ) by counting the number of decimal determined and by pushing normalized to values 1 to 2 ${\displaystyle x}$ ${\displaystyle x}$

The logarithm of then has the representation ${\displaystyle x}$

${\displaystyle {\begin{aligned}\log _{2}(x)&=0,b_{1}b_{2}b_{3}\cdots =\sum _{k>0}b_{k}2^{-k}{\text{ mit }}b_{k}\in \{0,1\}\\\log _{2}(x^{2})&=b_{1},b_{2}b_{3}\cdots \qquad {\text{ wegen }}\quad \log(x^{2})=2\log x.\end{aligned}}}$

So squaring shifts the logarithm one binary place to the left, which may make the integer digit one. This is the case if is. In this case, it is normalized again by division by 2, which has no effect on the remaining decimal places. This results in the following sketch of the process: ${\displaystyle x}$ ${\displaystyle x^{2}\geq 2}$ ${\displaystyle x}$

INPUT 1 ≤ x < 2
OUTPUT Nachkommastellen bi der Binärdarstellung von log2(x)

i ← 0
LOOP
   i ← i + 1
   x ← x2
   IF x ≥ 2 THEN
      x ← x / 2
      bi ← 1
   ELSE
      bi ← 0
   END IF
END LOOP

Analog computer

Simplified circuit diagram of a logarithmizer

To calculate the logarithm with the help of an analog computer - for example the generation of an electrical output voltage that takes the logarithm of the nominal value of the input voltage - one can make use of the exponential course of the current-voltage characteristic of a diode . The sketch opposite shows the basic structure of a logarithmizer with an operational amplifier , a diode and a resistor . ${\displaystyle U_{\text{a}}}$ ${\displaystyle U_{\text{e}}}$ ${\displaystyle D}$ ${\displaystyle R}$

Complex logarithm

Riemann surface of the complex logarithm function: The leaves reflect the ambiguity of the logarithm that follows from the periodicity of its inverse function, the exponential function.

Principal value of the logarithm ${\displaystyle \ln z}$

Analogous to the real definition, every complex number which the equation is called ${\displaystyle w}$

${\displaystyle \mathrm {e} ^{w}=z}$

satisfied, a natural logarithm of . There is one for each , but in contrast to the real logarithm because of ${\displaystyle z}$ ${\displaystyle z\in \mathbb {C} \setminus \{0\}}$ ${\displaystyle w}$

${\displaystyle \mathrm {e} ^{2k\pi \mathrm {i} }=1,\quad k\in \mathbb {Z} }$,

is not clearly determined. So if you found a logarithm of , so is that too ${\displaystyle w}$ ${\displaystyle z}$

${\displaystyle w'=\,\!w+2k\pi \mathrm {i} }$

with every integer a logarithm of , because it holds ${\displaystyle k}$ ${\displaystyle z}$

${\displaystyle \mathrm {e} ^{w'}=\mathrm {e} ^{w+2k\pi \mathrm {i} }=\mathrm {e} ^{w}\cdot \mathrm {e} ^{2k\pi \mathrm {i} }=\mathrm {e} ^{w}\cdot 1=\mathrm {e} ^{w}=z}$.

In order to achieve clarity, one selects from the possible values ​​for those values ​​that lie in a suitable strip of the complex number plane. You can z. B. the strip ${\displaystyle w}$

${\displaystyle \left\{w\in \mathbb {C} :-\pi <\operatorname {Im} \,w\leq \pi \right\}}$

use. A value of this strip is the main value ( English principal value ) of the logarithm, and to write . If you represent in polar form, you get a simple representation of the k-th branch of the logarithm function: ${\displaystyle w}$ ${\displaystyle w=\ln z}$ ${\displaystyle z=|z|\cdot \mathrm {e} ^{\mathrm {i} \arg z}}$

${\displaystyle w=\ln |z|+\mathrm {i} \left(\arg z+2k\pi \right),\quad k\in \mathbb {Z} }$

with the Argument function . The real logarithm already defined above is used in the summand . For one gets back the main branch of the complex logarithm: ${\displaystyle \arg }$ ${\displaystyle \ln |z|}$ ${\displaystyle \ln }$ ${\displaystyle k=0}$

${\displaystyle \ln z=\ln |z|+\mathrm {i} \arg z}$ .

${\displaystyle \ln }$is not steady on . However, if one removes the negative real axis, then the area is ${\displaystyle \mathbb {C} \setminus \{0\}}$ ${\displaystyle \ln }$

${\displaystyle \mathbb {C} \setminus \{x\in \mathbb {R} :x\leq 0\}}$

steady and even holomorphic .

Please note

For the main branch of the complex logarithm , not all of the calculation rules listed above for the real logarithm function apply . They only apply . This ambiguity is a direct consequence of the periodicity of its inverse function, the complex exponential function. The comparison of ${\displaystyle \ln }$ ${\displaystyle {\text{mod }}2\pi \mathrm {i} }$

${\displaystyle \ln(-1+\mathrm {i} )+\ln(-1+\mathrm {i} )=2{\bigl (}\ln {\sqrt {2}}+{\frac {3\pi }{4}}\mathrm {i} {\bigr )}=\ln 2+{\frac {3\pi }{2}}\mathrm {i} }$

With

${\displaystyle \ln(-1+\mathrm {i} )+\ln(-1+\mathrm {i} )=\ln {\bigl (}(-1+\mathrm {i} )(-1+\mathrm {i} ){\bigr )}=\ln(-2\mathrm {i} )=\ln 2-{\frac {\pi }{2}}\mathrm {i} }$

shows, that

${\displaystyle \ln x+\ln y=\ln(x\cdot y)}$

not for all of different complex numbers and is correct. The equation too ${\displaystyle 0}$ ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle y\cdot \ln x=\ln {x^{y}}}$

is not always fulfilled, like the counterexample

${\displaystyle 2\pi \mathrm {i} \ln \mathrm {e} =2\pi \mathrm {i} \;\neq \;0=\ln 1=\ln(\mathrm {e} ^{2\pi \mathrm {i} })}$

proves.

• Graphical representation of the complex logarithm
• 

  amount of ${\displaystyle \ln z}$

• 

  Real part of ${\displaystyle \ln z}$

• 

  Imaginary part of ${\displaystyle \ln z}$

The main branch of the complex logarithm defined above can be used to explain the logarithm of negative real numbers:

${\displaystyle \ln(-x)=\ln \left\vert -x\right\vert +\mathrm {i} \arg(-x)=\ln x+\mathrm {i} \pi ,\quad x\in \mathbb {R} ^{+}\ .}$

This assumes that the Argument function assigns the value to negative real numbers . ${\displaystyle \arg }$ ${\displaystyle \pi }$

These considerations show that the ambiguity of the complex logarithm is ultimately due to the ambiguity of the Argument function .

Discrete logarithms

→ Main article : Discrete logarithm

Discrete logarithms are solutions to equations of form

${\displaystyle a^{n}=\underbrace {a\circ a\circ \dotsb \circ a} _{n{\text{-mal}}}=b}$

over a finite cyclic group . The discrete logarithm from to the base is uniquely determined modulo the group order of and exists - since there is a producer of the group - for all elements of the group. ${\displaystyle (G,\circ )=\langle a\rangle }$ ${\displaystyle x}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle G}$ ${\displaystyle a}$

In the sense of complexity theory, discrete logarithms are complex to calculate for many groups and are used in cryptography , for example in cryptosystems based on elliptical curves .

Example:

${\displaystyle 2^{x}{\bmod {1}}1=5}$

has the value 4 as the solution, because 2 ⁴ = 16, and 16 leaves the remainder 5 when dividing with the remainder by 11. The solution is clearly modulo 10, i.e. modulo the group order of . Accordingly, there is also a solution of congruence. ${\displaystyle (\mathbb {Z} \,/\,11\,\mathbb {Z} )^{\times }}$ ${\displaystyle x}$ ${\displaystyle x\pm 10}$

See also

• Exponential function
• Euler's number
• Iterated logarithm
• Logarithmic spiral
• Chain logarithm
• Logarithmic paper
• Matrix logarithm
• Generalized logarithm

literature

• Charles Naux: Histoire des Logarithmes de Neper a Euler. Tome I, II, Blanchard, Paris 1966, 1971.
• Wolfgang Walter: Analysis I. Basic Knowledge of Mathematics Volume 3. Springer, Berlin 1985, ISBN 3-540-12780-1 .
• Klaus Jänich: Function Theory . An introduction. Springer, Berlin 2004, ISBN 3-540-20392-3 .
• IN Bronstein , KA Semendjajew , G. Musiol, H. Mühlig (Hrsg.): Taschenbuch der Mathematik . 10th, revised edition. Europa-Lehrmittel, Haan-Gruiten 2016, ISBN 978-3-8085-5790-7 .
• Ernst Hairer , Gerhard Wanner : Analysis in historical development . Springer-Verlag, Berlin / Heidelberg 2011, ISBN 978-3-642-13766-2 .

Web links

Wikibooks: Logarithmic Laws  - Learning and Teaching Materials

Wiktionary: Logarithm  - explanations of meanings, word origins, synonyms, translations

• Eric W. Weisstein : Logarithm . In: MathWorld (English).
• Logarithms
• Logarithms and logarithmic laws (online course, exercises, applets and links)

Individual evidence

1. ^ For example, C. Knott (Ed.): Napier Tercentenary Volume. 1915, p. 83 f.
2. ↑ Kathleen Clark, Clemency Montelle: Logarithms. The early history of a familiar function. On: MAA.org.
3. ^ John Napier: Mirifici logarithmorum canonis descriptio ejusque usus in utraque trigonometria etc. Edinburgh 1614 English translation by Ian Bruce from Napier: Mirifici Logarithmorum Canonis Descriptio. u. a.
4. ↑ Jeff Miller: Earliest Known Uses of Some of the Words of Mathematics (L). Retrieved August 29, 2009 . 
5. ^ Citations - Pierre-Simon De Laplace (1749-1827). Retrieved June 14, 2018 (French). 
6. ^ Scientific journal of the Humboldt University in Berlin. 38, 1989, p. 5.
7. ^ Lothar Kusch: Mathematik, Vol. 1: Arithmetik. Algebra, series theory, nomography. W. Girardet, Essen 1975, ISBN 3-7736-2755-6 , p. 162 f.
8. ↑ L. Lorentzen, H. Waadeland: A.2.2 The exponential function . (PDF) Continued Fractions . Atlantis Studies in Mathematics, 2008, p. 271. doi: 10.2991 / 978-94-91216-37-4 .
9. ↑ Since and are inverse functions of each other, the group axioms are easy to recalculate. The inverse of is because of the oddness of these functions ${\displaystyle \tanh }$ ${\displaystyle \operatorname {artanh} }$ ${\displaystyle \ominus u}$ ${\displaystyle u}$ ${\displaystyle =-u.}$