Integral logarithm

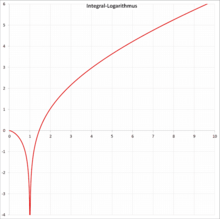
Function graph of in the range between 0 and 10 ${\displaystyle \operatorname {li} (x)}$

The logarithmic integral is an analytic function on the real numbers (or ) into the real numbers. It is of practical relevance in some areas of physics such as quantum field theory and in solving the Laplace equation in semiconductors, as well as in number theory , as it is closely linked to the density of prime numbers . ${\displaystyle x\geq 0,\;x\neq 1}$ ${\displaystyle x>1}$

definition

There are two common definitions that differ by a constant. For one of the most important applications - as an asymptotic comparison variable for the prime number function in the prime number theorem  - the difference between the two definitions does not matter.

One definition in the field is ${\displaystyle x\geq 0}$

${\displaystyle \operatorname {li} (x)=\int _{0}^{x}{\frac {\mathrm {d} t}{\ln t}}\ ,}$

it must because of the singularity in for a limit to be defined ( Cauchy principal value ): ${\displaystyle \operatorname {li} }$ ${\displaystyle x=1}$ ${\displaystyle x>1}$

${\displaystyle \operatorname {li} (x)=\lim _{\varepsilon \to 0^{+}}\left(\int _{0}^{1-\varepsilon }{\frac {\mathrm {d} t}{\ln t}}+\int _{1+\varepsilon }^{x}{\frac {\mathrm {d} t}{\ln t}}\right)\ .}$

Another definition for is ${\displaystyle x>1}$

${\displaystyle \operatorname {Li} (x)=\operatorname {li} (x)-\operatorname {li} (2)=\int _{2}^{x}{\frac {\mathrm {d} t}{\ln t}}\ .}$

There is no pole at , but a logarithmic singularity . ${\displaystyle x=1}$

properties

Function graph of in the range between 0 and 2 (includes 0, 1, µ and 2) ${\displaystyle \operatorname {li} (x)}$

Some values:

• ${\displaystyle \operatorname {li} (0)=0}$
• ${\displaystyle \operatorname {li} (1)=-\infty }$
• ${\displaystyle \operatorname {li} (\mu )=0}$
• ${\displaystyle \operatorname {li} (2)=1{,}04516\;37801\;17492\;78484\ldots }$(Follow A069284 in OEIS )

Here (sequence A070769 in OEIS ) is the Ramanujan-Soldner constant . ${\displaystyle \mu =1{,}45136\;92348\;83381\;05028\ldots }$

It applies with the integral exponential function , from which one obtains the series representation ${\displaystyle \operatorname {li} (x)=\operatorname {Ei} (\ln x)}$ ${\displaystyle \operatorname {Ei} }$

${\displaystyle \operatorname {li} (x)=\gamma +\ln \left|\ln x\right|+\sum _{k=1}^{\infty }{\frac {(\ln x)^{k}}{k\cdot k!}}\ ,}$

where (sequence A001620 in OEIS ) is the Euler-Mascheroni constant . ${\displaystyle \gamma =0{,}57721\;56649\;01532\;86060\ldots }$

From the definition of , one obtains through linear substitution ${\displaystyle \operatorname {li} }$

${\displaystyle \operatorname {li} (x)=x\int _{0}^{1}{\frac {\mathrm {d} t}{\ln(x\,t)}}\ ,}$

where for, because of the singularity, Cauchy's principal value must be used. We also have for ${\displaystyle x>1}$ ${\displaystyle t=1/x}$
${\displaystyle x\geq 0,x\neq 1}$

${\displaystyle \int _{0}^{x}\operatorname {li} (t)\,{\mathrm {d} t}=x\,\operatorname {li} (x)-\operatorname {li} (x^{2}).}$

Also applies to ${\displaystyle p>-1,p\not =0}$

${\displaystyle \int _{0}^{1}\operatorname {li} (t)\,t^{p-1}\,\mathrm {d} t=-{\tfrac {1}{p}}\ln(p+1),}$

for one obtains In the limiting case is ${\displaystyle p=1}$ ${\displaystyle \textstyle \int _{0}^{1}\operatorname {li} (t)\,\mathrm {d} t=-\ln 2.}$
${\displaystyle p=0}$ ${\displaystyle \textstyle \int _{0}^{1}\operatorname {li} (t)\,t^{-1}\,\mathrm {d} t=-1.}$

Another formula is ${\displaystyle \textstyle \int _{0}^{1}\operatorname {li} (t^{-1})\,t\,\mathrm {d} t=\textstyle \int _{1}^{\infty }\operatorname {li} (t)\,t^{-3}\,\mathrm {d} t=0.}$

The Golomb-Dickman constant (sequence A084945 in OEIS ) occurs in the theory of random permutations when estimating the length of the longest cycle of a permutation and in number theory when estimating the size of the largest prime factor of a number. ${\displaystyle \lambda =\textstyle \int _{0}^{1}\mathrm {e} ^{\operatorname {li} (x)}\mathrm {d} x=0{,}62432\;99885\;43550\;87099\ldots }$

Asymptotic behavior

Function graph of in the range between 1 and 10 ¹³ ${\displaystyle \operatorname {li} (x)}$

For big ones it can ${\displaystyle x}$ ${\displaystyle \operatorname {li} (x)}$

${\displaystyle \operatorname {li} (x)=0!\,{\frac {x}{\ln x}}+1!\,{\frac {x}{\ln ^{2}x}}+2!\,{\frac {x}{\ln ^{3}x}}+3!\,{\frac {x}{\ln ^{4}x}}+\dotsb }$

approximate . The series is an asymptotic development ; it does not converge , but rather approaches the true value and then moves away again. The best approximation is achieved after roughly terms, then the summands become larger due to the increasing effect of the factorial . ${\displaystyle \ln x}$

See also

• Integral sine
• Integral cosine

literature

• Johann Georg Soldner : Théorie et tables d'une nouvelle fonction transcendante . Lindauer, Munich 1809 (French; on Google Books )
• Niels Nielsen : Theory of the logarithmic integral and related transcendent , BG Teubner, Leipzig 1906 ( archive.org )

Web links

• Eric W. Weisstein : Logarithmic Integral . In: MathWorld (English).
• Logarithmic integral . at The Wolfram Functions Site (English; with calculation option)