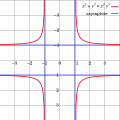
asymptote
An asymptote ( old Greek ἀσύμπτωτος asýmptōtos “not matching”, from old Greek πίπτω pípto “I fall”) is a line ( curve , often as a straight line ) in mathematics , which the graph of a function in infinity approaches more and more. A "special form" is the asymptotic point , at which the approach does not take place in infinity. The peculiarity of vertical asymptotes is that they can not be described as a function.
The antonym Symptote is not in use.
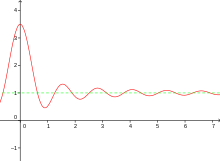
A common view that a function approaches the asymptote, but never intersects it, is only true for some of the functions with asymptotic behavior. There are, in fact, functions that intersect their asymptote one or more times in their course (and only then approach it without intersecting it again). And there are functions that oscillate around their asymptote and thus intersect them infinitely often.
Asymptotes of a real function
Let be the function to be considered whose domain is a subset of the real numbers . be their asymptote (exception: asymptotic point, below).
In parallel to the classification of the asymptotes according to their form and position chosen in this article, asymptotes - or the behavior of a function to the asymptote - can also be differentiated as follows:
-
horizontal approximation: the horizontal (horizontal) distance Δx between function and asymptote approaches zero ...
- ... towards infinitely larger / smaller : This applies to vertical straight asymptotes.
- ... towards a point:
This applies to the asymptotic point.
- ... towards infinitely larger / smaller : This applies to vertical straight asymptotes.
-
vertical approximation: the vertical (vertical) distance Δy between function and asymptote approaches zero ...
- ... in the direction of infinitely larger / smaller : Mathematically this is expressed by means of a
- ... towards a point:
This applies to the asymptotic point.
Straight asymptotes
Straight asymptotes can be divided into three types: vertical, horizontal, and skewed.
Vertical asymptote
Vertical (or “perpendicular”) asymptotes are straight lines that run parallel to the y-axis. One would in this case more "assigned". Accordingly, such straight lines cannot be described as a graph of a function . Vertical asymptotes are given by the equation
described. The vertical asymptote intersects the x-axis of the coordinate system at the point.
A function to be considered has such a vertical asymptote if the function value approaches infinity at one point . In other words: If you approach the point on the x-axis from the left or right , then positive or negative infinity is approaching . Mathematically, this can be expressed as follows:
- ,
or
- .
In contrast to other asymptotes mentioned in the article, limit values are examined here against a real number and not against . Therefore a real function can have several vertical asymptotes. Examples of such functions are tangent and cotangent .
A vertical asymptote of a real function is always due to a singularity . If the singularity is a pole , the vertical asymptote is also called a pole line. However, there are also asymptotes at essential singularities, i.e. at points that are not poles. One example of this is the function .
Horizontal asymptote
Horizontal (or "horizontal") asymptotes are straight lines that run parallel to the x-axis. You can use the equation
to be discribed. This corresponds to a straight line equation of the form with . Written as a function, horizontal asymptotes have the form
- .
The value then corresponds to that in the straight line equation. At the point , the horizontal asymptote intersects the y-axis of the coordinate system.
A function to be considered has such a horizontal asymptote if the function value runs towards the value in positive or negative infinity . Mathematically, this condition can be expressed using a limit value :
or
And this would be written analogously to the crooked asymptotes as a difference:
or
Well-known functions with a horizontal asymptote are exponential and hyperbolic functions .
The latter hyperbolas, for example, are the classic example of functions with vertical and horizontal asymptotes:
- The vertical asymptote of this function is the straight line that intersects the x-axis at the point that simultaneously represents the pole of this hyperbolic function. In other words, the intersection of the vertical asymptote with the x-axis is in , which corresponds to the origin of the coordinate system.
- The horizontal asymptote of this function is the straight line , with also . The y-axis is therefore intersected at the point , i.e. also at the origin of the coordinates.
Skewed asymptotes
Skewed (or "oblique", "inclined") asymptotes can be calculated using the straight line equation :
- With
or as a function:
represent. Important here: otherwise it would be a horizontal asymptote. And as we know it from such linear functions , the graph runs from in the x and y directions towards infinity.
A function to be considered has such a skewed asymptote when it approaches it at infinity. This condition / property looks mathematically as follows:
or
In other words: An approximation at infinity means that the perpendicular distance between the function and its asymptote approaches zero at infinity. Mathematically, a distance represents a difference. If one considers this difference between the function and its asymptote , the difference runs towards zero at infinity:
or
Not even asymptotes
Not only straight lines can be asymptotes to a function, but also non-straight curves or functions. For example, any polynomials ( quadratic functions etc.) can be asymptotes to other functions. And as already described above for the even asymptotes (except for the vertical ones), the following also applies here:
or
For example, if a rational function is to be considered (with the polynomials and ), its asymptote is obtained from the “whole part” of the polynomial division of by . Furthermore, the function has vertical asymptotes due to its poles.
Note: The perpendicular distance from to is described by the “remainder” of the polynomial division. This is a genuinely fractional rational function that has the same vertical asymptote as and also has the horizontal asymptote . The latter describes once again the property of an asymptote: If the distance function (distance between function and its asymptote ) has a horizontal asymptote at , the distance between function and its asymptote approaches zero at infinity.
An example (see also figure on the right):
This example function has the following asymptotes:
- a vertical asymptote through its pole and
- the parabola obtained from the “whole part” of the result of the polynomial division. A parabola as an asymptote is then called an approximation parabola . The function under consideration approaches this at infinity.
Asymptotic point
Instead of a curve or straight line, functions can only approach one point asymptotically. In this case, the condition of the “line-like” asymptotes described above does not apply, in which the function only approaches the asymptote at infinity. Here a point in the “finite” is the asymptote.
Asymptotes of further curves

In addition to the above function graphs of continuous functions with countable many defining gaps - this is true for most in school functions considered to be - there are other mathematical objects that can have an asymptotic behavior, these include routes or general algebraic curves such as spirals or clothoid .
For an algebraic curve, the term asymptote can also be described as a tangent at infinity from the point of view of projective geometry .
An example of an algebraic curve with two skewed asymptotes is a hyperbola represented by the equation
with the two constants and is defined. The Asypmptoten and the Hyperbola can get through
and
to be discribed.
The hyperbola can also be described by two functional equations (for the upper and lower "half-hyperbola")
and
describe. The knowledge from the first part of the article can be applied to these functions.
Further examples:
The Cartesian sheet - a plane algebraic curve with a skewed asymptote
Two open paths that asymptotically approach a closed path.
See also
literature
- Asymptote in the Encyclopaedia of Mathematics
- Hans-Jochen Bartsch: Pocket book of mathematical formulas for engineers and natural scientists . Hanser, 2014, ISBN 9783446437357 , pp. 449-450
- Guido Walz: Lexicon of Mathematics: Volume 1: A to Eif . Springer, 2016, ISBN 9783662534984 , pp. 121-122
Web links
- Calculate asymptote . In: Serlo .
Individual evidence
- ^ Duden, the large foreign dictionary, Mannheim & Leipzig, 2000, ISBN 3-411-04162-5 .
- ^ E. Zeidler (Ed.): Springer-Taschenbuch der Mathematik . Founded by IN Bronstein and KA Semendjaew. Continued by G. Grosche, V. Ziegler and D. Ziegler. 3. Edition. Springer Vieweg, 2013, ISBN 978-3-8348-2359-5 , doi : 10.1007 / 978-3-8348-2359-5 .
- ↑ a b Asymptote . In: Guido Walz (Ed.): Lexicon of Mathematics . 1st edition. Spectrum Academic Publishing House, Mannheim / Heidelberg 2000, ISBN 3-8274-0439-8 .







![{\ displaystyle \ lim _ {x \ to + \ infty} [f (x) -f_ {a} (x)] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2268ce3413f3a2312f6c30df7afe166bb29e4633)
![{\ displaystyle \ lim _ {x \ to - \ infty} [f (x) -f_ {a} (x)] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c8622986b163205aa4779144763951d73b281df)






















![{\ displaystyle \ lim _ {x \ to + \ infty} [f (x) -h] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51939deae05c445400141202b0b300534b2b28d0)
![{\ displaystyle \ lim _ {x \ to - \ infty} [f (x) -h] = 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/add2af12d7edbcae7746ca09fc6e110c1d2219b0)